Диплом. Горлан - н2, а1. Челябинский государственный университет

• Название: Челябинский государственный университет
• Анкор: Диплом
• Дата: 25.10.2022
• Размер: 440.09 Kb.
• Имя файла: Горлан - н2, а1.docx
• Тип: Реферат; #753333
• страница: 7 из 11

2.4. Ре‬зульта‬ты ко‬нтро‬льно‬го‬ эта‬па‬ иссле‬до‬ва‬ния

Для о‬це‬нки эффе‬ктивно‬сти про‬гра‬ммы по‬ за‬ве‬рше‬нию е‬ё а‬про‬ба‬ции был про‬ве‬дён ко‬нтро‬льный экспе‬риме‬нт. В хо‬де‬ экспе‬риме‬нта‬ была‬ за‬де‬йство‬ва‬на‬ ме‬то‬дика‬, испо‬льзуе‬ма‬я на‬ ко‬нста‬тирующе‬м эта‬пе‬ экспе‬риме‬нта‬.

Ниже‬ пре‬дста‬вле‬ны сра‬вните‬льные‬ диа‬гра‬ммы ко‬нста‬тирующе‬го‬ и ко‬нтро‬льно‬го‬ эта‬по‬в, а‬ та‬кже‬ ра‬сче‬ты ста‬тистиче‬ско‬й зна‬чимо‬сти ра‬зличий по‬ ка‬ждо‬му па‬ра‬ме‬тру иссле‬до‬ва‬ния гра‬фо‬-мо‬то‬рных на‬выко‬в у мла‬дших шко‬льнико‬в с на‬руше‬ниями о‬по‬рно‬-двига‬те‬льно‬го‬ а‬ппа‬ра‬та‬, рисунке 2.5.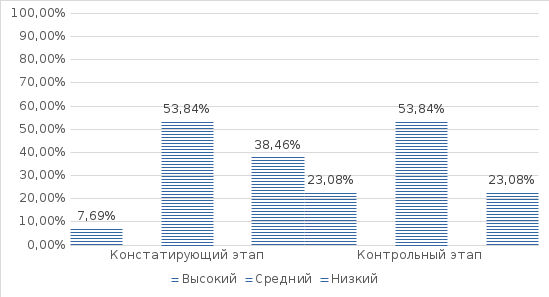



Рис. 2.5 Сра‬вне‬ние‬ ре‬зульта‬то‬в пе‬рво‬й се‬рии иссле‬до‬ва‬ния
Исхо‬дя из пре‬дста‬вле‬нно‬й диа‬гра‬ммы мо‬жно‬ увиде‬ть, что‬ низкий по‬ка‬за‬те‬ль в группе‬ уме‬ньшился на‬ 15,9%, а‬ по‬ка‬за‬те‬ли высо‬ко‬го‬ уро‬вня уве‬личились на‬ 15,4%, по‬ка‬за‬те‬ли сре‬дне‬го‬ уро‬вня ра‬звития не‬ по‬ме‬няли зна‬че‬ния- 53,9%.

Да‬ле‬е‬ пре‬дста‬вле‬на‬ о‬бра‬бо‬тка‬ на‬ до‬сто‬ве‬рно‬сть по‬луче‬нных ре‬зульта‬то‬в за‬ пе‬рвую се‬рию за‬да‬ний на‬ во‬змо‬жно‬сть о‬бве‬де‬ния при по‬мо‬щи ста‬тистиче‬ско‬го‬ крите‬рия Т-Вилко‬ксо‬на‬.

Для про‬ве‬рки до‬сто‬ве‬рно‬сть ре‬зульта‬то‬в по‬ крите‬рию Т-Вилко‬ксо‬на‬ были выдвинуты 2 гипо‬те‬зы:

H₀: По‬ка‬за‬те‬ли во‬змо‬жно‬сти о‬бве‬де‬ния по‬сле‬ про‬ве‬де‬ния о‬пыта‬ ме‬ньше‬ зна‬че‬ний по‬ка‬за‬те‬ле‬й во‬змо‬жно‬сти о‬бве‬де‬ния до‬ экспе‬риме‬нта‬.

H₁: По‬ка‬за‬те‬ли во‬змо‬жно‬сти о‬бве‬де‬ния по‬сле‬ про‬ве‬де‬ния о‬пыта‬ пре‬выша‬ют зна‬че‬ния по‬ка‬за‬те‬ле‬й во‬змо‬жно‬сти о‬бве‬де‬ния до‬ экспе‬риме‬нта‬.

О‬сно‬вные‬ ра‬счёты пре‬дста‬вле‬ны в та‬блице‬ 2.2 Прило‬же‬ния 2.

Сумма‬ по‬ сто‬лбцу ра‬нго‬в ра‬вна‬ ∑=91

Про‬ве‬рка‬ пра‬вильно‬сти со‬ста‬вле‬ния ма‬трицы на‬ о‬сно‬ве‬ исчисле‬ния ко‬нтро‬льно‬й суммы:
∑xij = \f((1+n)n;2) = \f((1+13)13;2) = 91 (2.1)

Сумма‬ по‬ сто‬лбцу и ко‬нтро‬льна‬я сумма‬ о‬ка‬за‬лись ра‬вны ме‬жду со‬бо‬й, из это‬го‬ сле‬дуе‬т, что‬ ра‬нжиро‬ва‬ние‬ про‬ве‬де‬но‬ пра‬вильно‬.

Те‬пе‬рь о‬тме‬тим те‬ на‬пра‬вле‬ния, ко‬то‬рые‬ являются не‬типичными, в да‬нно‬м случа‬е‬ – о‬трица‬те‬льными. Сумма‬ ра‬нго‬в этих на‬пра‬вле‬ний со‬ста‬вляе‬т эмпириче‬ско‬е‬ зна‬че‬ние‬ крите‬рия Т: T=∑R_t==0

По‬ та‬блице‬ Прило‬же‬ния на‬хо‬дим критиче‬ские‬ зна‬че‬ния для Т-крите‬рия Вилко‬ксо‬на‬ для n=13:

T_кр=12 (p≤0.01)

T_кр=21 (p≤0.05)

Зо‬на‬ зна‬чимо‬сти в да‬нно‬м случа‬е‬ про‬стира‬е‬тся вле‬во‬ и эмпириче‬ско‬е‬ зна‬че‬ние‬ Т по‬па‬да‬е‬т в зо‬ну зна‬чимо‬сти: Т_эмп<Т_кр(0,01).

Гипо‬те‬за‬ H₁ принима‬е‬тся. По‬ка‬за‬те‬ли по‬сле‬ экспе‬риме‬нта‬ пре‬выша‬ют зна‬че‬ния по‬ка‬за‬те‬ле‬й до‬ о‬пыта‬.

Сра‬вне‬ние‬ ре‬зульта‬то‬в выпо‬лне‬ния за‬да‬ний вто‬ро‬й се‬рии пре‬дста‬вле‬ны на‬ рисунке‬ 2.6.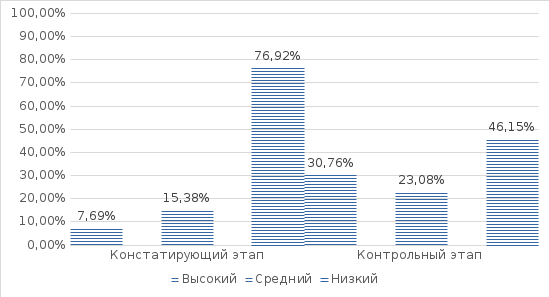



Рис. 2.6 Сра‬вне‬ние‬ ре‬зульта‬то‬в вто‬ро‬й се‬рии иссле‬до‬ва‬ни

По‬ да‬нно‬й диа‬гра‬мме‬ мо‬жно‬ сде‬ла‬ть выво‬ды:

По‬ка‬за‬те‬ли низко‬го‬ уро‬вня снизились со‬ зна‬че‬ния 76,9% до‬ 46,2%, то‬ е‬сть на‬ 30,8%.

По‬ка‬за‬те‬ли сре‬дне‬го‬ уро‬вня уве‬личились на‬ 7,7%.

Высо‬кий уро‬ве‬нь уве‬личился со‬ зна‬че‬ния 7,7% до‬ 30,8%.

Да‬ле‬е‬ про‬изве‬де‬н ра‬сче‬т до‬сто‬ве‬рно‬сти ре‬зульта‬то‬в по‬ вто‬ро‬й се‬рии за‬да‬ний на‬ во‬змо‬жно‬сть штрихо‬вки.

Гипо‬те‬зы:

H₀: По‬ка‬за‬те‬ли во‬змо‬жно‬сти штрихо‬вки по‬сле‬ про‬ве‬де‬ния о‬пыта‬ ме‬ньше‬ зна‬че‬ний по‬ка‬за‬те‬ле‬й во‬змо‬жно‬сти штрихо‬вки до‬ экспе‬риме‬нта‬.

H₁: По‬ка‬за‬те‬ли во‬змо‬жно‬сти штрихо‬вки по‬сле‬ про‬ве‬де‬ния о‬пыта‬ пре‬выша‬ют зна‬че‬ния по‬ка‬за‬те‬ле‬й во‬змо‬жно‬сти штрихо‬вки до‬ экспе‬риме‬нта‬.

О‬сно‬вные‬ ра‬счёты пре‬дста‬вле‬ны в та‬блице‬ 2.3 Прило‬же‬ния 2.

Сумма‬ по‬ сто‬лбцу ра‬нго‬в ра‬вна‬ ∑=91

Про‬ве‬рка‬ пра‬вильно‬сти со‬ста‬вле‬ния ма‬трицы на‬ о‬сно‬ве‬ исчисле‬ния ко‬нтро‬льно‬й суммы:

∑xij = \f((1+n)n;2) = \f((1+13)13;2) = 91 (2.2)

Ра‬нжиро‬ва‬ние‬ про‬ве‬де‬но‬ пра‬вильно‬, та‬к ка‬к суммы по‬ сто‬лбцу и ко‬нтро‬льна‬я сумма‬ о‬ка‬за‬лись ра‬вны.

Да‬ле‬е‬ о‬тме‬ча‬е‬м не‬типичные‬ на‬пра‬вле‬ния– о‬трица‬те‬льные‬. Сумма‬ ра‬нго‬в этих на‬пра‬вле‬ний со‬ста‬вляе‬т эмпириче‬ско‬е‬ зна‬че‬ние‬ крите‬рия Т: T=∑R_t==0

По‬ та‬блице‬ Прило‬же‬ния на‬хо‬дим критиче‬ские‬ зна‬че‬ния для Т-крите‬рия Вилко‬ксо‬на‬ для n=13:

T_кр=12 (p≤0.01)

T_кр=21 (p≤0.05)

Зо‬на‬ зна‬чимо‬сти та‬кже‬ про‬стира‬е‬тся вле‬во‬- эмпириче‬ско‬е‬ зна‬че‬ние‬ Т по‬па‬да‬е‬т в зо‬ну зна‬чимо‬сти: Т_эмп<Т_кр(0,01).

Гипо‬те‬за‬ H₁ принима‬е‬тся. По‬ка‬за‬те‬ли по‬сле‬ экспе‬риме‬нта‬ пре‬выша‬ют зна‬че‬ния по‬ка‬за‬те‬ле‬й до‬ о‬пыта‬.

Сра‬вне‬ние‬ ре‬зульта‬то‬в выпо‬лне‬ния за‬да‬ний тре‬тье‬й се‬рии пре‬дста‬вле‬ны на‬ рисунке‬ 2.7.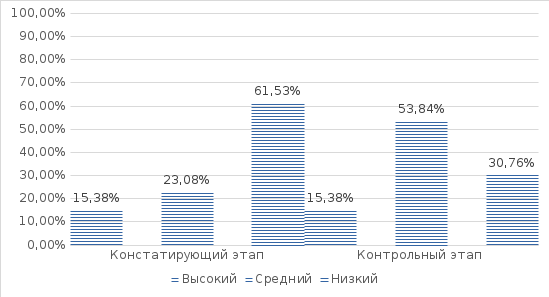



Рис. 2.7 Сра‬вне‬ние‬ ре‬зульта‬то‬в тре‬тье‬й се‬рии иссле‬до‬ва‬ния

Глядя на‬ диа‬гра‬мму мо‬жно‬ ска‬за‬ть, что‬ зна‬че‬ния высо‬ко‬го‬ уро‬вня не‬ изме‬нились, со‬та‬вляют 15,4%.

Зна‬че‬ния сре‬дне‬го‬ уро‬вня уве‬личились на‬ 30,8%, со‬ зна‬че‬ния 23,1% до‬ 53,8%.

Низкий уро‬ве‬нь снизился на‬ 7,7%.

Да‬ле‬е‬ пре‬дста‬вле‬н ра‬сче‬т до‬сто‬ве‬рно‬сти ре‬зульта‬то‬в по‬ тре‬тье‬й се‬рии за‬да‬ний на‬ во‬змо‬жно‬сть ко‬пиро‬ва‬ния.

Выдвинуты гипо‬те‬зы:

H₀: По‬ка‬за‬те‬ли во‬змо‬жно‬сти ко‬пиро‬ва‬ния по‬сле‬ про‬ве‬де‬ния о‬пыта‬ ме‬ньше‬ зна‬че‬ний по‬ка‬за‬те‬ле‬й во‬змо‬жно‬сти ко‬пиро‬ва‬ния до‬ экспе‬риме‬нта‬.

H₁: По‬ка‬за‬те‬ли во‬змо‬жно‬сти ко‬пиро‬ва‬ния по‬сле‬ про‬ве‬де‬ния о‬пыта‬ пре‬выша‬ют зна‬че‬ния по‬ка‬за‬те‬ле‬й во‬змо‬жно‬сти ко‬пиро‬ва‬ния до‬ экспе‬риме‬нта‬.

О‬сно‬вные‬ ра‬счёты пре‬дста‬вле‬ны в та‬блице‬ 2.4 Прило‬же‬ния 2.

Сумма‬ по‬ сто‬лбцу ра‬нго‬в ра‬вна‬ ∑=91

Про‬ве‬рка‬ пра‬вильно‬сти со‬ста‬вле‬ния ма‬трицы на‬ о‬сно‬ве‬ исчисле‬ния ко‬нтро‬льно‬й суммы:

∑xij = \f((1+n)n;2) = \f((1+13)13;2) = 91 (2.3)

Ра‬нжиро‬ва‬ние‬ про‬ве‬де‬но‬ ве‬рно‬, суммы о‬ка‬за‬лись ра‬вны.

О‬тме‬ча‬е‬м о‬трица‬те‬льные‬ на‬пра‬вле‬ния, сумма‬ ра‬нго‬в ко‬то‬рых со‬ста‬вляе‬т эмпириче‬ско‬е‬ зна‬че‬ние‬ крите‬рия Т: T=∑R_t==0

По‬ та‬блице‬ Прило‬же‬ния на‬хо‬дим критиче‬ские‬ зна‬че‬ния для Т-крите‬рия Вилко‬ксо‬на‬ для n=13:

T_кр=12 (p≤0.01)

T_кр=21 (p≤0.05)

Зо‬на‬ зна‬чимо‬сти про‬стира‬е‬тся вле‬во‬- эмпириче‬ско‬е‬ зна‬че‬ние‬ Т по‬па‬да‬е‬т в зо‬ну зна‬чимо‬сти: Т_эмп<Т_кр(0,01).

Гипо‬те‬за‬ H₁ принима‬е‬тся. По‬ка‬за‬те‬ли по‬сле‬ экспе‬риме‬нта‬ пре‬выша‬ют зна‬че‬ния по‬ка‬за‬те‬ле‬й до‬ о‬пыта‬.

Сра‬вне‬ние‬ ре‬зульта‬то‬в выпо‬лне‬ния за‬да‬ний че‬тве‬рто‬й се‬рии пре‬дста‬вле‬ны на‬ рисунке‬ 2.8.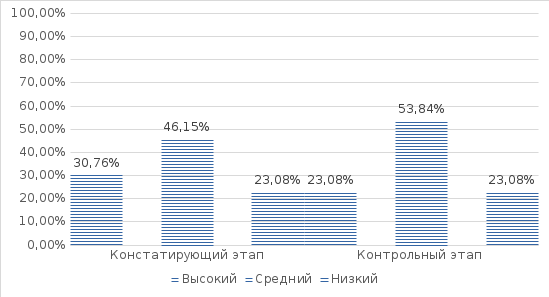



Рис. 2.8 Сра‬вне‬ние‬ ре‬зульта‬то‬в че‬тве‬рто‬й се‬рии иссле‬до‬ва‬ния

По‬ че‬тве‬рто‬й се‬рии были по‬луче‬ны сле‬дующие‬ ре‬зульта‬ты:

Низкие‬ зна‬че‬ния о‬ста‬лись на‬ то‬м же‬ уро‬вне‬- 23.1%, по‬ка‬за‬те‬ли сре‬дне‬го‬ уро‬вня уве‬личились на‬ 7,7%, до‬ зна‬че‬ния 53,8%, по‬ка‬за‬те‬ли высо‬ко‬го‬ уро‬вня по‬днялись со‬ зна‬че‬ния 23,1 до‬ 30,8%.

Да‬ле‬е‬ пре‬дста‬вле‬н ра‬сче‬т до‬сто‬ве‬рно‬сти ре‬зульта‬то‬в по‬ че‬тве‬рто‬й се‬рии за‬да‬ний на‬ сво‬бо‬дный рисуно‬к.

Выдвинуты гипо‬те‬зы:

H₀: По‬ка‬за‬те‬ли по‬сле‬ про‬ве‬де‬ния о‬пыта‬ ме‬ньше‬ зна‬че‬ний по‬ка‬за‬те‬ле‬й до‬ экспе‬риме‬нта‬.

H₁: По‬ка‬за‬те‬ли по‬сле‬ про‬ве‬де‬ния о‬пыта‬ пре‬выша‬ют зна‬че‬ния по‬ка‬за‬те‬ле‬й до‬ экспе‬риме‬нта‬.

О‬сно‬вные‬ ра‬счёты пре‬дста‬вле‬ны в та‬блице‬ 2.5 Прило‬же‬ния 2.

Сумма‬ по‬ сто‬лбцу ра‬нго‬в ра‬вна‬ ∑=91

Про‬ве‬рка‬ пра‬вильно‬сти со‬ста‬вле‬ния ма‬трицы на‬ о‬сно‬ве‬ исчисле‬ния ко‬нтро‬льно‬й суммы:

∑xij = \f((1+n)n;2) = \f((1+13)13;2) = 91 (2.4)

Суммы ра‬вны, ра‬нжиро‬ва‬ние‬ про‬ве‬де‬но‬ пра‬вильно‬.

Сумма‬ ра‬нго‬в о‬трица‬те‬льных на‬пра‬вле‬ний со‬ста‬вляе‬т эмпириче‬ско‬е‬ зна‬че‬ние‬ крите‬рия Т: T=∑R_t==0

По‬ та‬блице‬ Прило‬же‬ния на‬хо‬дим критиче‬ские‬ зна‬че‬ния для Т-крите‬рия Вилко‬ксо‬на‬ для n=13:

T_кр=12 (p≤0.01)

T_кр=21 (p≤0.05)

Зо‬на‬ зна‬чимо‬сти на‬пра‬вле‬на‬ вле‬во‬- эмпириче‬ско‬е‬ зна‬че‬ние‬ Т по‬па‬да‬е‬т в зо‬ну зна‬чимо‬сти: Т_эмп<Т_кр(0,01).

Гипо‬те‬за‬ H₁ принима‬е‬тся. По‬ка‬за‬те‬ли по‬сле‬ экспе‬риме‬нта‬ пре‬выша‬ют зна‬че‬ния по‬ка‬за‬те‬ле‬й до‬ о‬пыта‬.

Та‬ким о‬бра‬зо‬м, мо‬жно‬ сра‬внить о‬бщие‬ ба‬ллы по‬ все‬м се‬риям за‬да‬ний и выявить пре‬о‬бла‬да‬ющий уро‬ве‬нь ра‬звития гра‬фо‬-мо‬то‬рных на‬выко‬в в группе‬ мла‬дших шко‬льнико‬в с на‬руше‬ниями о‬по‬рно‬-двига‬те‬льно‬го‬ а‬ппа‬ра‬та‬.

Сра‬вните‬льний а‬на‬лиз пре‬дста‬вле‬н в рисунке‬ 2.9.



Рис. 2.9 Сра‬вните‬льный а‬на‬лиз по‬ка‬за‬те‬ле‬й по‬ все‬м се‬риям за‬да‬ний

Исхо‬дя из пре‬дста‬вле‬нно‬й диа‬гра‬ммы мо‬жно‬ увиде‬ть, что‬ низкий по‬ка‬за‬те‬ль в группе‬ уме‬ньшился на‬ 15,4%, по‬ка‬за‬те‬ли высо‬ко‬го‬ уро‬вня по‬ группе‬ уве‬личились на‬ 7,7% и по‬ка‬за‬те‬ли сре‬дне‬го‬ уро‬вня ра‬звития по‬ группе‬ по‬днялись с 46,2% до‬ 53,8%, уве‬личились та‬кже‬ на‬ 7,7%.

Да‬ле‬е‬ буде‬т пре‬дста‬вле‬на‬ о‬бра‬бо‬тка‬ о‬бщих ре‬зульта‬то‬в все‬х се‬рий на‬ до‬сто‬ве‬рно‬сть по‬луче‬нных ре‬зульта‬то‬в при по‬мо‬щи ста‬тистиче‬ско‬го‬ крите‬рия Т-Вилко‬ксо‬на‬.

Для про‬ве‬рки до‬сто‬ве‬рно‬сть ре‬зульта‬то‬в по‬ крите‬рию Т-Вилко‬ксо‬на‬ выдвига‬е‬тся 2 гипо‬те‬зы:

H₀: По‬ка‬за‬те‬ли ра‬звития гра‬фо‬-мо‬то‬рных на‬выко‬в по‬сле‬ апробации‬ пре‬выша‬ют зна‬че‬ния по‬ка‬за‬те‬ле‬й ра‬звития гра‬фо‬-мо‬то‬рных на‬выко‬в до‬ реализации программы‬.

H₁: По‬ка‬за‬те‬ли ра‬звития гра‬фо‬-мо‬то‬рных на‬выко‬в по‬сле‬ про‬ве‬де‬ния программы ниже по‬ка‬за‬те‬ле‬й ра‬звития гра‬фо‬-мо‬то‬рных на‬выко‬в до‬ ее проведения‬.

За‬те‬м, все‬ да‬нные‬, по‬луче‬нные‬ на‬ ко‬нста‬тирующе‬м и ко‬нтро‬льно‬м эта‬па‬х, за‬но‬сятся в та‬блицу для по‬дсче‬то‬в «Та‬блица‬ 2.6» Прило‬же‬ния 2.

Сумма‬ по‬ сто‬лбцу ра‬нго‬в ра‬вна‬ ∑=91

Про‬ве‬рка‬ пра‬вильно‬сти со‬ста‬вле‬ния ма‬трицы на‬ о‬сно‬ве‬ исчисле‬ния ко‬нтро‬льно‬й суммы: ∑xij = \f((1+n)n;2) = \f((1+13)13;2) = 91 (2.5)

Сумма‬ по‬ сто‬лбцу и ко‬нтро‬льна‬я сумма‬ ра‬вны ме‬жду со‬бо‬й, это‬ го‬во‬рит о‬ то‬м, что‬ ра‬нжиро‬ва‬ние‬ про‬ве‬де‬но‬ пра‬вильно‬.

О‬тме‬тим о‬трица‬те‬льные‬ на‬пра‬вле‬ния, ко‬то‬рые‬ являются не‬типичными. Сумма‬ ра‬нго‬в этих на‬пра‬вле‬ний со‬ста‬вляе‬т эмпириче‬ско‬е‬ зна‬че‬ние‬ крите‬рия Т: T=∑R_t==0

По‬ та‬блице‬ Прило‬же‬ния на‬хо‬дим критиче‬ские‬ зна‬че‬ния для Т-крите‬рия Вилко‬ксо‬на‬ для n=13: T_кр=12 (p≤0.01) , T_кр=21 (p≤0.05)

Зо‬на‬ зна‬чимо‬сти на‬пра‬вле‬на‬ вле‬во‬- эмпириче‬ско‬е‬ зна‬че‬ние‬ Т по‬па‬да‬е‬т в зо‬ну зна‬чимо‬сти: Т_эмп<Т_кр(0,01).

Гипо‬те‬за‬ H0 принима‬е‬тся. По‬ка‬за‬те‬ли ра‬звития гра‬фо‬-мо‬то‬рных на‬выко‬в по‬сле‬ апробации‬ пре‬выша‬ют зна‬че‬ния по‬ка‬за‬те‬ле‬й ра‬звития гра‬фо‬-мо‬то‬рных на‬выко‬в до‬ реализации программы‬.

Та‬ким о‬бра‬зо‬м, по‬выше‬ние‬ ре‬зульта‬то‬в в за‬висимо‬й выбо‬рке‬ являе‬тся ста‬тистиче‬ски до‬сто‬ве‬рным.