|
|
вавм. Билеты методы математический физики 2022 фипк-211. Дайте определение скалярного поля. Приведите примеры скалярного поля. Покажите как графически изображается скалярное поле. Приведите примеры.
13-Билет
№
|
|
1
|
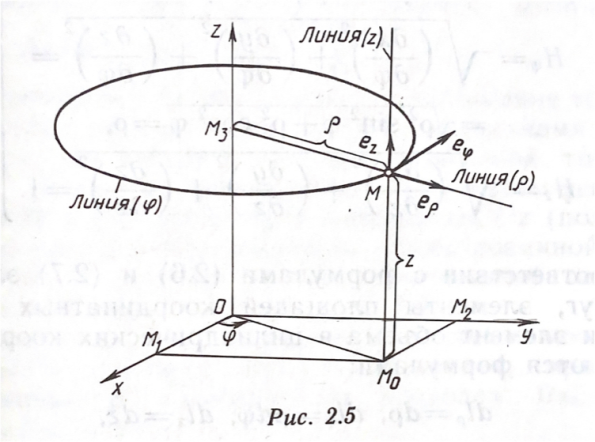
Назовите цилиндрические координаты. Покажите связь цилиндрических и декартовых координат. Сделайте рисунок и покажите координатные поверхности и координатные линии в цилиндрической системе координат. Определите коэффициенты Ламе в цилиндрической системе координат и выразите элементы длин дуг соответствующих координатных линий, элементы площадей координатных поверхностей и элемент объема при помощи этих коэффициентов. Запишите основные дифференциальные операции в цилиндрических координатах.
При решении задач часто встречаются две системы криволинейных координат: цилиндрическая и сферическая.
В цилиндрической системе координат положение точки 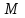 пространства определяется тремя величинами: расстоянием пространства определяется тремя величинами: расстоянием 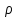 от точки от точки 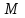 до фиксированной прямой до фиксированной прямой 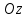 ; углом ; углом 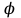 , образованным фиксированной плоскостью , образованным фиксированной плоскостью 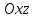 и полуплоскостью, ограниченной осью и полуплоскостью, ограниченной осью 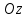 и проходящей через фиксированную точку и проходящей через фиксированную точку 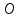 этой прямой. В цилиндрической системе координат этой прямой. В цилиндрической системе координат 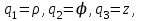 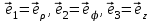 , причем , причем 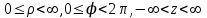 . .
Связь декартовых координат точки с ее цилиндрическими координатами выражается соотношениями 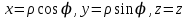 . .
Координатными поверхностями в случае цилиндрической системы координат являются: 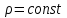 – цилиндры с осью – цилиндры с осью 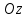 ; ;
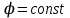 – полуплоскости, ограниченные осью – полуплоскости, ограниченные осью 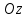 ; ; 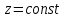 – плоскости, перпендикулярные к – плоскости, перпендикулярные к 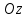 . .
Координатными линиями будут: линии 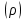 – лучи, перпендикулярные к оси – лучи, перпендикулярные к оси 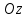 с началом на этой оси; линии с началом на этой оси; линии 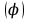 – окружности с центрами на оси – окружности с центрами на оси 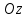 и радиусами и радиусами 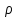 , плоскости которых перпендикулярны к этой оси; линии , плоскости которых перпендикулярны к этой оси; линии 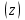 – прямые, параллельные оси – прямые, параллельные оси 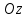 . .
Коэффициенты Ламе в цилиндрической системе координат определяются следующим образом:
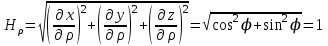 , ,
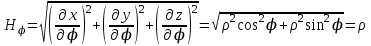 , ,
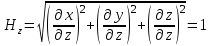 . .
Элементы длин дуг соответствующих координатных линий, элементы площадей координатных поверхностей и элемент объема в цилиндрической системе координат с учетом коэффициентов Ламе выражаются формулами:
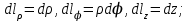 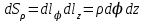 , ,
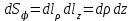 , , 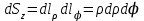 , ,
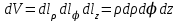 . .
Для основных дифференциальных операций в цилиндрической системе координат получаются следующие выражения:
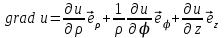 ; ;
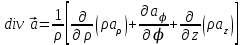 ; ;
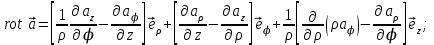
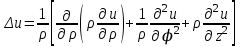 . .
|
2
|
Запишите уравнение Пуассона для потенциала электростатического поля. Сформулируйте граничное условие для данной задачи. Примените метод функции Грина для определения потенциала электростатического поля.
Выражение векторного поля через потенциал электростатического поля:
то есть:
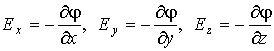 , ,
|
(1.66)
|
и подставить выражение (1.65) в формулу:
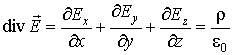
то получим уравнение:
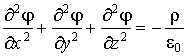 . .
|
(1.67)
|
Уравнение (1.67) называют уравнением Пуассона, в частном случае оно превращается в уравнение Лапласа. В операторной форме уравнение Пуассона имеет вид:
Это уравнение, выведенное впервые Пуассоном, однозначно определяет потенциал φ если учесть естественное граничное условие . Частный случай уравнения Пуассона при ρ=0
называется уравнением Лапласа.
Метод функции Грина для определения потенциала электростатического поля .
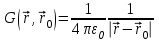 . .
Пусть 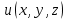 - потенциал электростатического поля, создаваемого во всем пространстве электрическими зарядами, распределенными с плотностью - потенциал электростатического поля, создаваемого во всем пространстве электрическими зарядами, распределенными с плотностью 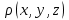 в заданном конечном объеме в заданном конечном объеме 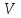 . В этом случае краевое условие имеет вид . В этом случае краевое условие имеет вид 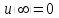 , а искомое решение удовлетворяет уравнению Пуассона , а искомое решение удовлетворяет уравнению Пуассона
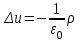 . .
Поле полностью определяется распределением заряда 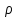 , поэтому решение ищем в виде , поэтому решение ищем в виде
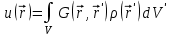 , ,
где 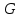 - решение задачи для точечного источника, т.е. поля, создаваемого точечным единичным зарядом. Распределение такого заряда выражается функцией - решение задачи для точечного источника, т.е. поля, создаваемого точечным единичным зарядом. Распределение такого заряда выражается функцией
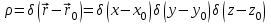 , ,
где 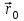 - точка, в которой находится заряд. Поэтому - точка, в которой находится заряд. Поэтому 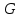 удовлетворяет уравнению удовлетворяет уравнению
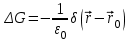 . .
Функция Грина представляет собой потенциал электростатического поля в точке 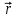 , создаваемый единичным точечным зарядом, помещенным в точку с радиусом-вектором , создаваемый единичным точечным зарядом, помещенным в точку с радиусом-вектором 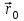 . Следовательно, в рассматриваемом случае функцию Грина согласно знаниям из электростатики можем записать в виде . Следовательно, в рассматриваемом случае функцию Грина согласно знаниям из электростатики можем записать в виде
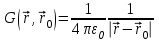 . .
Тогда решение задачи для произвольного распределения заряда определяется по формуле
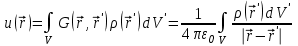 , ,
|
|
14-Билет
№
|
|
1
|
Дайте определение вектор-функции скалярного аргумента. Приведите примеры вектор-функций из разных разделов физики. Запишите правила дифференцирования вектор-функции. Приведите правила интегрирования вектор-функции.
Если каждому допустимому значению скалярного аргумента 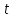 соответствует определенное значение модуля и определенное направление вектора в пространстве, то говорят, что задана вектор-функция скалярного аргумента соответствует определенное значение модуля и определенное направление вектора в пространстве, то говорят, что задана вектор-функция скалярного аргумента 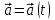 . .
Задание вектор-функции 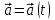 равносильно заданию трех скалярных функций – координат вектора равносильно заданию трех скалярных функций – координат вектора 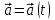 : :
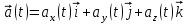 . .
В физике часто используются переменные векторы, зависящие от скалярного аргумента. Например, сила может быть функцией времени или координат, напряженность электрического или гравитационного поля – функцией координат и т.д.
Правила дифференцирования вектор-функции:
1.Если 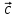 – постоянный вектор, то – постоянный вектор, то 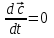 . .
2.Если 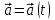 , , 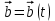 – вектор-функции, то – вектор-функции, то
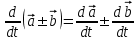 . .
3.Если 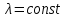 , то , то
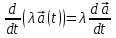 . .
4.Если 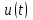 – скалярная функция, то – скалярная функция, то
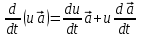 . .
5.Если 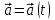 , , 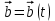 – вектор-функции, то – вектор-функции, то
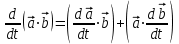 . .
6.Если 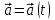 , , 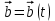 – вектор-функции, то – вектор-функции, то
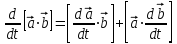 . .
7.Если 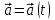 , , 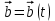 , , 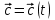 – вектор-функции, то – вектор-функции, то
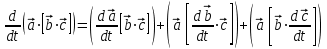 . .
8.Если 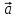 – функция скаляра – функция скаляра 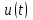 , то , то
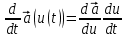 . .
Основные правила интегрирования вектор-функции:
1. 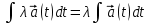 , где , где 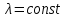 . .
2. 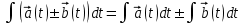 . .
3. 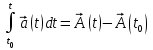 , где , где 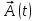 – некоторая первообразная для – некоторая первообразная для 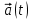 на отрезке на отрезке 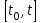
|
2
|
Назовите физические задачи, описываемые уравнениями параболического типа. Перечислите методы решения уравнений параболического типа и с помощью одного из них решите уравнение данного типа.
Уравнения параболического типа получаются при исследовании таких физических явлений, как теплопроводность, диффузия, распространение электромагнитных полей в проводящих средах, движение вязкой жидкости. К уравнениям параболического типа относятся уравнения теплопроводности, уравнения диффузии. Они могут быть одномерными, двумерными или трехмерными, однородными или неоднородными.
К методам решения уравнений параболического типа относятся: метод разделения переменных-метод Фурье, операционный метод (Лапласа)
Применим метод Фурье для уравнения теплопроводности(параболический тип).
Рассмотрим простейший процесс такого типа – охлаждение бесконечного стержня. В начальный момент времени температура неравномерно нагретого длинного стержня задана функцией 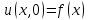 . Требуется найти распределение температур для любого . Требуется найти распределение температур для любого 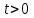 . Стержень очень длинный, поэтому температурные условия на его концах можно не учитывать. При отсутствии тепловых источников температура различных точек стержня определяется уравнением . Стержень очень длинный, поэтому температурные условия на его концах можно не учитывать. При отсутствии тепловых источников температура различных точек стержня определяется уравнением
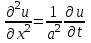 . .
Для решения задачи воспользуемся методом разделения переменных. Представив решение в виде
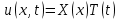 , получим , получим
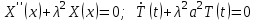 . .
Решение этих уравнений имеет вид:
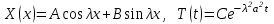 . .
В результате получаем следующее семейство частных решений уравнения
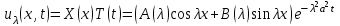 . .
Так как с течением времени температура стержня не может возрастать, показатель экспоненты в 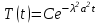 должен быть отрицательным. Следовательно, должен быть отрицательным. Следовательно, 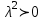 и и 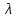 - вещественное число. Причем - вещественное число. Причем 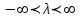 . Чтобы получить решение, удовлетворяющее начальному условию, надо взять суперпозицию частных решений, соответствующих различным значениям . Чтобы получить решение, удовлетворяющее начальному условию, надо взять суперпозицию частных решений, соответствующих различным значениям  . Но так как в рассматриваемом случае . Но так как в рассматриваемом случае 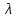 изменяется непрерывно, сумму нужно заменить интегралом: изменяется непрерывно, сумму нужно заменить интегралом:
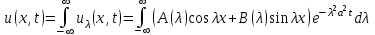 , ,
Неизвестные функции 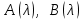 должны быть такими, чтобы выполнялось условие должны быть такими, чтобы выполнялось условие 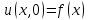 : :
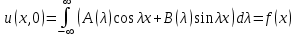
Это интеграл Фурье. Используя теорию интегралов Фурье, найдем
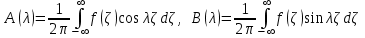 . .
| |
|
|
 Скачать 3.75 Mb.
Скачать 3.75 Mb.