20-Билет
№
|
|
1
|
Ответьте на вопрос о том, что изучает математическая физика. Назовите основные задачи математической физики. Сформулируйте основные задачи математической физики.
Математическая физика является интегративной дисциплиной, которая обьединяет математику и физику в обьеме, необходимом для изучения разделов теоретической физики.
Математическая физика представляет собой теорию математических модолей физических явлений.
В математической физике рассматриваются две задачи- прямая и обратная.
Прямая задача состоит в следующем. Задано правило определения рассматриваемой физической велечины в любой точке пространства, т.е. характер поля. Изучением дифференциальных свойств различных полей занимается математическая теория поля.
Обратная задача состоит в определении конкретного вида математического поля, если извесны условия, в которых находится физическое тело.
|
2
|
Напишите уравнение Бесселя. Изложите методику решения уравнения Бесселя. Назовите цилиндрические функции.
Цилиндрические функции: функция Бесселя, функция Грина
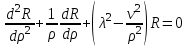
Это уравнение называется уравнением Бесселя.
 
|
21-Билет
№
|
|
1
|
Дайте определение производной скалярного поля. Найдите зависимость производной скалярного поля от направления дифференцирования.
Вектор, направленный в данной точке 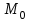 по нормали к поверхности уровня в сторону возрастания скалярного поля и численно равный производной скалярного поля в точке по нормали к поверхности уровня в сторону возрастания скалярного поля и численно равный производной скалярного поля в точке 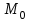 по нормали, называется градиентом скалярного поля: по нормали, называется градиентом скалярного поля:
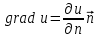
Градиент поля имеет следующие дифференциальные свойства
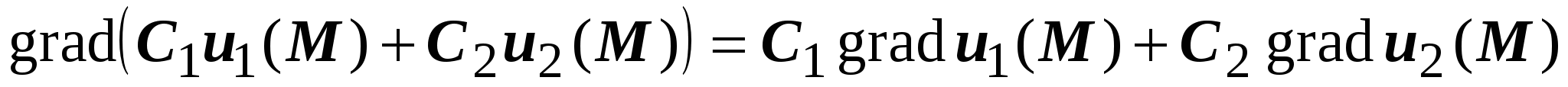 , или , или 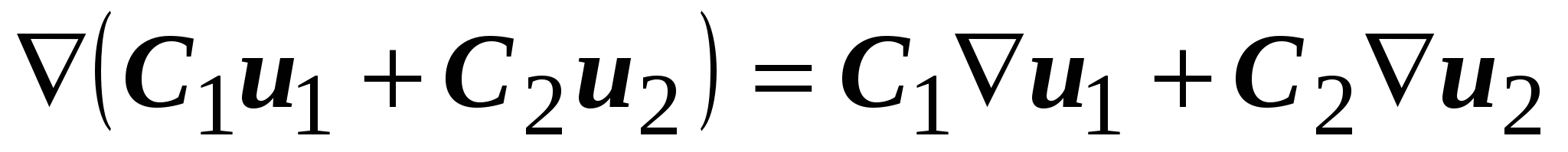 ; ;
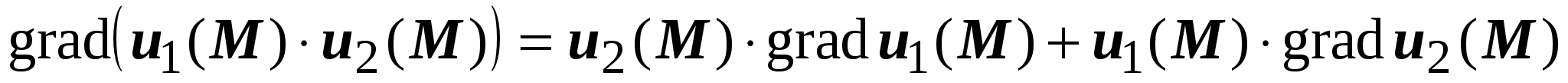 , или , или 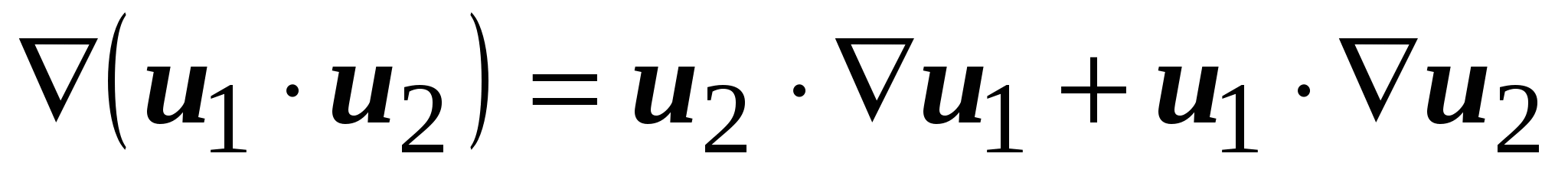 ; ;
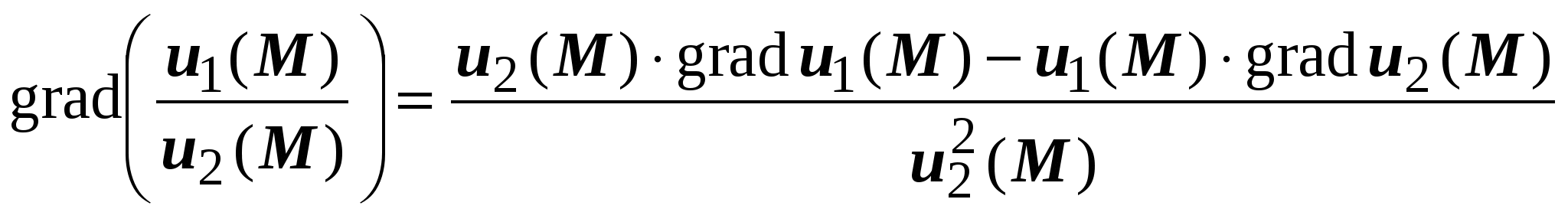 , или , или 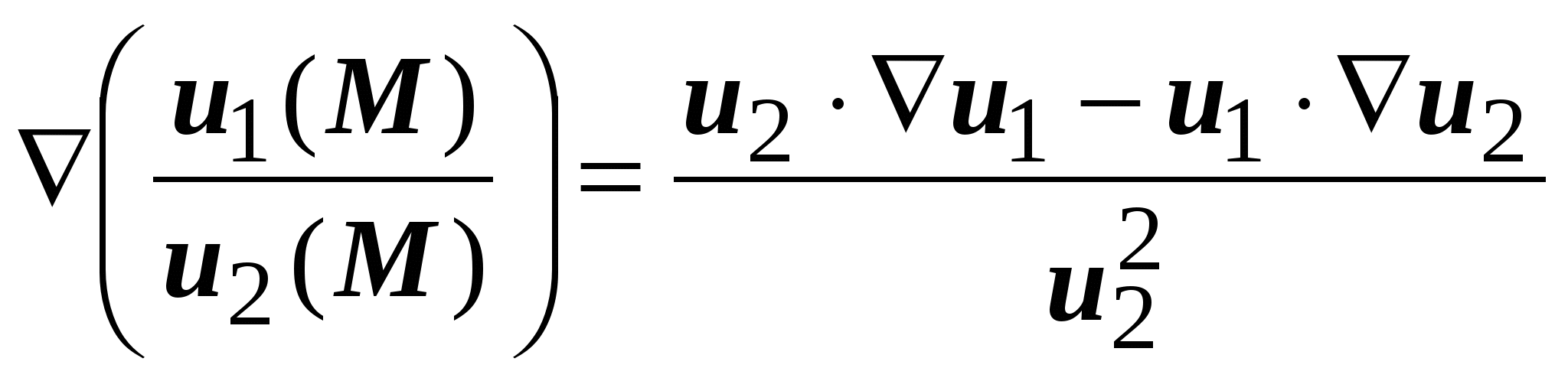 ; ;
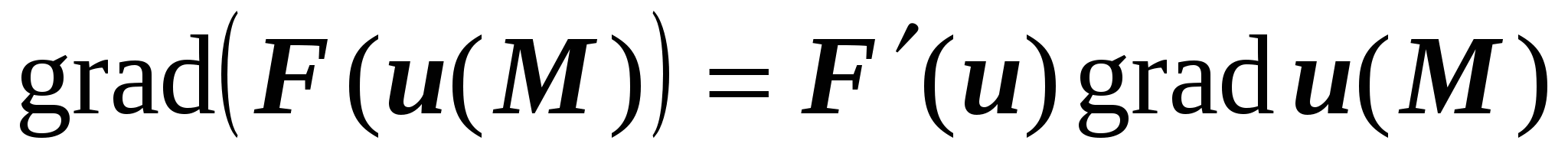 , или , или 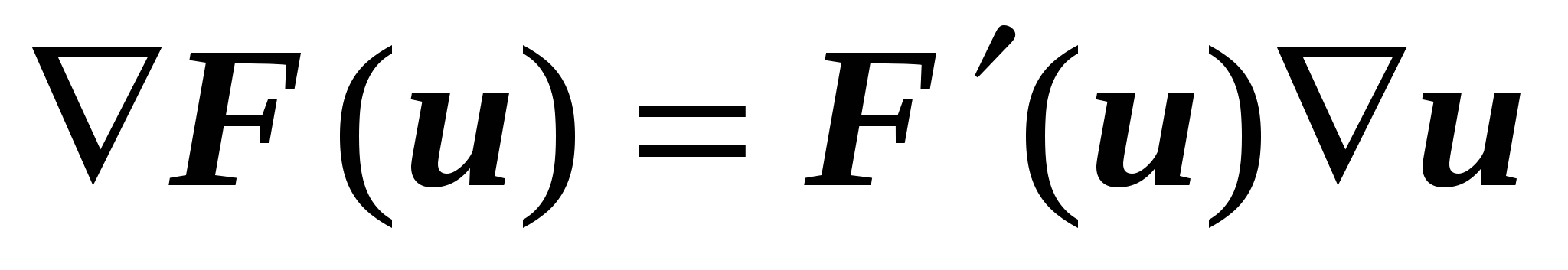 , ,
которые легко доказываются применением обычных правил дифференцирования.
|
2
|
Напишите уравнение Лежандра. Изложите методику решения уравнения Лежандра. Запишите формулы Родриго для полиномов Лежандра и присоединенных полиномов Лежандра.
Обобщенное уравнение Лежандра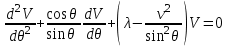 . .
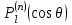 - присоединенные полиномы Лежандра, вычисляемые по формуле Родриго - присоединенные полиномы Лежандра, вычисляемые по формуле Родриго
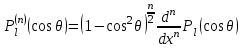
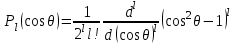 - полиномы Лежандра.. - полиномы Лежандра..
 
|
22-Билет
№
|
|
1
|
Запишите оператор Гамильтона. Найдите результат действия оператора Гамильтона на произведения скалярных и векторных полей. Используя аналитический метод, определить результат действия оператора Гамильтона на произведение скалярного и векторного полей 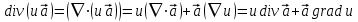
Оператор Гамильтона
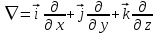
Результат действия оператора Гамильтона на произведения скалярных и векторных полей следующий:
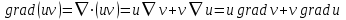 ; (1) ; (1)
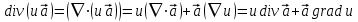 ; (2) ; (2)
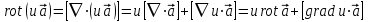 . (3) . (3)
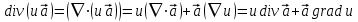
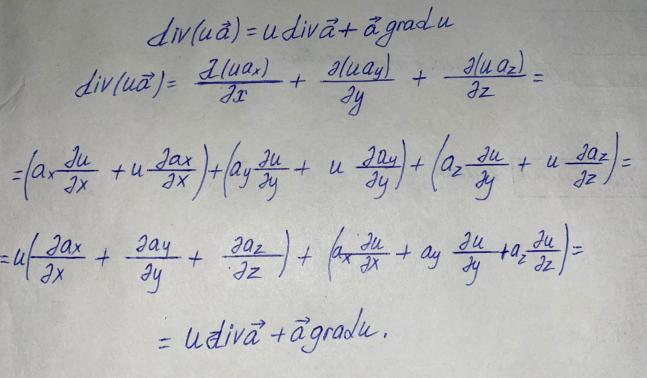
|
2
|
Дайте определение уравнения гиперболического типа. Приведите примеры уравнений гиперболического типа. Покажите как уравнение гиперболического типа приводится к каноническому виду.
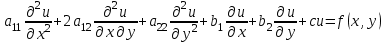 (1) (1)
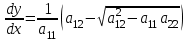 (2) (2) 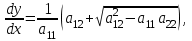 (3) (3)
В зависимости от значения коэффициентов, стоящих при старших производных, уравнения подразделяются на несколько типов.Если 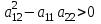 , то дифференциальное уравнение в частных производных называется уравнением гиперболического типа. , то дифференциальное уравнение в частных производных называется уравнением гиперболического типа.
Если уравнение (3.1) гиперболического типа, то интегралы 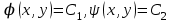 уравнений (3.3) и (3.4) вещественны и различны. Они определяют два различных семейства вещественных характеристик уравнения (3.1). С помощью замены переменных уравнений (3.3) и (3.4) вещественны и различны. Они определяют два различных семейства вещественных характеристик уравнения (3.1). С помощью замены переменных 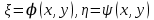 уравнение (3.1) приводят к каноническому виду уравнения гиперболического типа: уравнение (3.1) приводят к каноническому виду уравнения гиперболического типа:
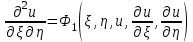 . .
К уравнениям гиперболического типа относятся:
трехмерное волновое уравнение 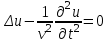 , где , где 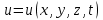 , ,
одномерное волновое уравнение (уравнение колебаний струны) 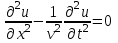 , где , где 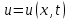 , ,
неоднородное волновое уравнение (уравнение Даламбера) 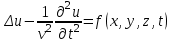 . .
|
23-Билет
№
|
|
1
|
Назовите дифференциальные операции второго порядка. Произведите доказательство одного из результатов дифференциальных операций второго порядка непосредственным вычислением.
Дифференциальные операции второго порядка получаются в результате двукратного применения оператора Гамильтона к скалярному и векторному полю.
Дифференциальные операции второго порядка можно представить в виде таблицы:
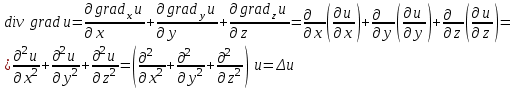
|
2
|
Дайте определение уравнения параболического типа. Приведите примеры уравнений параболического типа. Покажите как уравнение параболического типа приводится к каноническому виду.
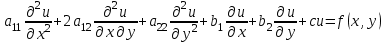 (1) (1)
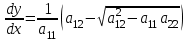 (2) (2) 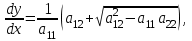 (3) (3)
В зависимости от значения коэффициентов, стоящих при старших производных, уравнения подразделяются на несколько типов.Если 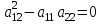 , то – уравнением параболического типа. , то – уравнением параболического типа.
Если же уравнение (1) параболического типа, то уравнения (2) и (3) совпадают, и мы получаем один общий интеграл характеристического уравнения : 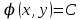 , определяющий одно семейство вещественных характеристик уравнения (1). Произведя замену переменных по формулам , определяющий одно семейство вещественных характеристик уравнения (1). Произведя замену переменных по формулам 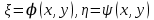 , где , где 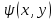 — такая функция, что — такая функция, что 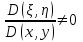 в рассматриваемой области, приведем уравнение (1) к виду в рассматриваемой области, приведем уравнение (1) к виду
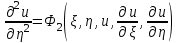
называемому каноническим видом уравнения параболического типа.
Уравнения параболического типа получаются при исследовании таких физических явлений, как теплопроводность, диффузия, распространение электромагнитных полей в проводящих средах, движение вязкой жидкости. К уравнениям параболического типа относятся уравнения теплопроводности, уравнения диффузии. Они могут быть одномерными, двумерными или трехмерными, однородными или неоднородными.
Одномерная задача о распределении температуры в стержне приводится к исследованию уравнения теплопроводности, которое в общем виде может быть представлено в виде: 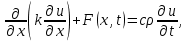
где 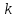 - коэффициент теплопроводности, зависящий от свойств материала, - коэффициент теплопроводности, зависящий от свойств материала, 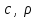 - удельная теплоемкость и плотность вещества, - удельная теплоемкость и плотность вещества, 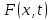 - функция плотности тепловых источников. - функция плотности тепловых источников.
Если стержень однородный, это уравнение примет вид: 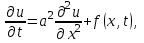
где 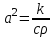 - коэффициент температуропроводности, - коэффициент температуропроводности, 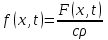 . .
Если объемные источники тепла отсутствуют, то получим
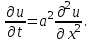
| |
 Скачать 3.75 Mb.
Скачать 3.75 Mb.
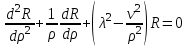


 по нормали к поверхности уровня в сторону возрастания скалярного поля и численно равный производной скалярного поля в точке
по нормали к поверхности уровня в сторону возрастания скалярного поля и численно равный производной скалярного поля в точке 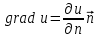
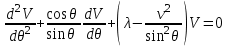 .
. 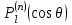 - присоединенные полиномы Лежандра, вычисляемые по формуле Родриго
- присоединенные полиномы Лежандра, вычисляемые по формуле Родриго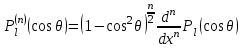
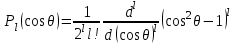 - полиномы Лежандра..
- полиномы Лежандра..

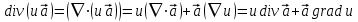
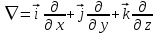
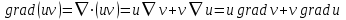 ; (1)
; (1)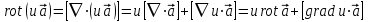 . (3)
. (3)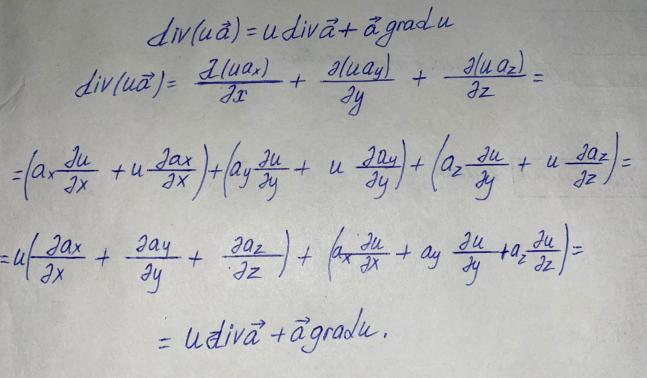
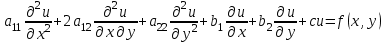 (1)
(1)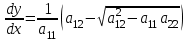 (2)
(2) 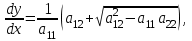 (3)
(3)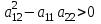 , то дифференциальное уравнение в частных производных называется уравнением гиперболического типа.
, то дифференциальное уравнение в частных производных называется уравнением гиперболического типа.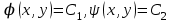 уравнений (3.3) и (3.4) вещественны и различны. Они определяют два различных семейства вещественных характеристик уравнения (3.1). С помощью замены переменных
уравнений (3.3) и (3.4) вещественны и различны. Они определяют два различных семейства вещественных характеристик уравнения (3.1). С помощью замены переменных 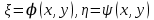 уравнение (3.1) приводят к каноническому виду уравнения гиперболического типа:
уравнение (3.1) приводят к каноническому виду уравнения гиперболического типа: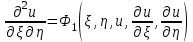 .
.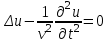 , где
, где 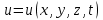 ,
,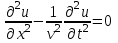 , где
, где 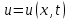 ,
,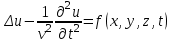 .
.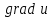
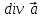
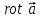
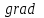
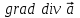
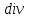
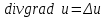
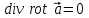
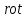
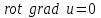
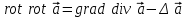
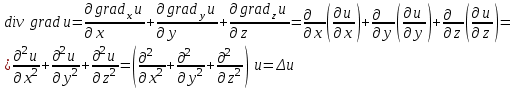
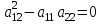 , то – уравнением параболического типа.
, то – уравнением параболического типа.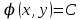 , определяющий одно семейство вещественных характеристик уравнения (1). Произведя замену переменных по формулам
, определяющий одно семейство вещественных характеристик уравнения (1). Произведя замену переменных по формулам 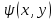 — такая функция, что
— такая функция, что 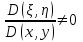 в рассматриваемой области, приведем уравнение (1) к виду
в рассматриваемой области, приведем уравнение (1) к виду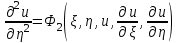
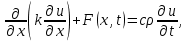
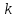 - коэффициент теплопроводности,
- коэффициент теплопроводности, 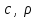 - удельная теплоемкость и плотность вещества,
- удельная теплоемкость и плотность вещества, 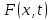 - функция плотности тепловых источников.
- функция плотности тепловых источников. 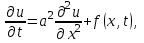
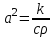 - коэффициент температуропроводности,
- коэффициент температуропроводности, 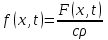 .
.