Билет
№
|
Вопросы/задания
|
1
|
Дайте определение скалярного поля.Приведите примеры скалярного поля.Покажите как графически изображается скалярное поле.Приведите примеры.Дайте инвариантное определение градиента скалярного поля.Перечислите основные свойства градиента скалярного поля.Покажите как вычисляется модуль градиента скалярного поля.
Если каждой точке пространства поставлено в соответствие определенное значение некоторой скалярной величины, то говорят, что в этом пространстве определено скалярное поле этой величины.
Примерами скалярных полей являются поля температур (воздуха, тела
и т.д.), атмосферного давления, плотности (массы, воздуха и т.д.), электрического потенциала и т.д.
Графически скалярное поле изображается с помощью эквипотенциальных поверхностей. Совокупность точек, в которых скалярное поле имеет одинаковое значение, называется поверхностью уровня или эквипотенциальной поверхностью. Уравнения эквипотенциальных поверхностей имеют вид:
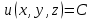 , , 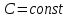
Например, в поле точечного электрического заряда поверхностями уровня электростатического потенциала являются концентрические сферы, а в поле заряженного бесконечного цилиндра – коаксиальные цилиндры.
Градиентом скалярного поля u (x, y, z) называется вектор, проекциями которого на координатные оси служат значения соответствующих частных производных этой функции, то есть
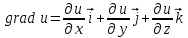 , , 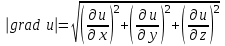 , , 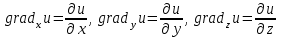
Градиент является основной характеристикой скалярного поля и обладает следующими свойствами:
1) 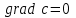 , где – постоянная; , где – постоянная;
2) 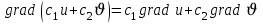 , где , где 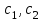 - постоянные; - постоянные;
3) 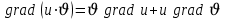 ; ;
4) 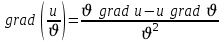 ; ;
5) 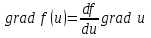 . .
|
2
|
Запишите уравнение Лапласа в цилиндрических координатах. Найдите решение этого уравнения методом Фурье. Назовите специальные функции, которые встречаются при решении данного уравнения.
Уравнение Лапласа в цилиндрических координатах имеет следующий вид:
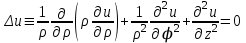 (4.1) (4.1)
Решение этого уравнения ищем методом Фурье. Положим, что
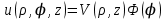 (4.2) (4.2)
и подставим это произведение в уравнение (4.1). Тогда получим два уравнения
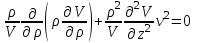 (4.3) (4.3)
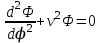 (4.4) (4.4)
К первому уравнению еще раз применим метод Фурье. Пусть
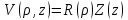 (4.5) (4.5)
Для функций 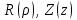 получим следующие обыкновенные дифференциальные уравнения получим следующие обыкновенные дифференциальные уравнения 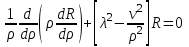 (4.6) (4.6)
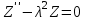 (4.7) (4.7)
Общие решения уравнений (4.4) и (4.7) имеют вид:
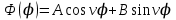 (4.8) (4.8)
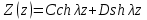 (4.9) (4.9)
Уравнение (4.6) можно представить в виде
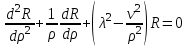
| 2-Билет
№
|
Вопросы/задания
|
1
|
В математической физике используют основные формулы векторной алгебры. Дайте определения скалярного и векторного произведений двух векторов.Приведите их основные свойства.Выразите скалярное и векторное произведения двух векторов через проекции на координатные оси.Запишите формулу двойного векторного произведения. Покажите основное свойство смешанного произведения трех векторов.
Основные формулы векторной алгебры, применяемые в физических приложениях:
1. Разложение вектора 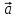 по ортам по ортам 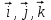 прямоугольной декартовой системы координат прямоугольной декартовой системы координат 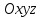 : :
где 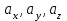 – координаты вектора . – координаты вектора .
2. Длина вектора 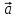 : : 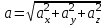
.
3. Скалярное произведение двух векторов 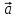 и и 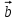 : :
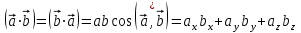
где 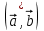 - угол между векторами - угол между векторами 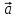 и и 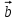 . .
4. Векторное произведение двух векторов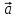 и и 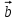 : :
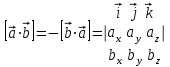 , ,
длина которого равна 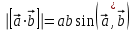
5. Смешанное произведение трех векторов 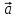 , , 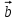 и и 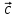 : :
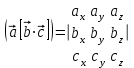 . .
Основное свойство смешанного произведения трех векторов:
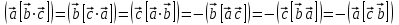
6. Двойное векторное произведение трех векторов 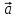 , , 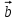 и и 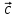 : :
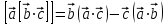
.
7. Произведения, содержащие более двух векторов:
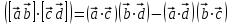
8. Тождество Эйлера-Лагранжа:
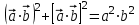
9. Условие ортогональности двух векторов 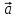 и и 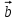 : :
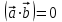
10. Условие коллинеарности двух векторов 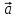 и и 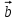 : :
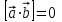
11. Условие компланарности трех векторов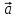 , , 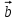 и и 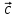 : :
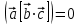
.
|
2
|
Рассмотрите задачу об охлаждении бесконечно длинного стержня. Решите задачу методом Фурье.
Рассмотрим простейший процесс такого типа – охлаждение бесконечного стержня. В начальный момент времени температура неравномерно нагретого длинного стержня задана функцией . Требуется найти распределение температур для любого . Стержень очень длинный, поэтому температурные условия на его концах можно не учитывать. При отсутствии тепловых источников температура различных точек стержня определяется уравнением 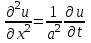
Для решения задачи воспользуемся методом разделения переменных. Представив решение в виде 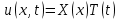 , получим , получим
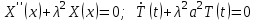 . .
Решение этих уравнений имеет вид: 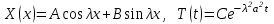
.
В результате получаем следующее семейство частных решений уравнения 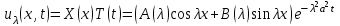
Так как с течением времени температура стержня не может возрастать, показатель экспоненты в 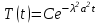 должен быть отрицательным. Следовательно, должен быть отрицательным. Следовательно, 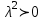 и и 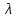 - вещественное число. Причем - вещественное число. Причем 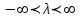 . Чтобы получить решение, удовлетворяющее начальному условию, надо взять суперпозицию частных решений, соответствующих различным значениям . Чтобы получить решение, удовлетворяющее начальному условию, надо взять суперпозицию частных решений, соответствующих различным значениям 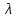 . Но так как в рассматриваемом случае . Но так как в рассматриваемом случае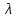 изменяется непрерывно, сумму нужно заменить интегралом: изменяется непрерывно, сумму нужно заменить интегралом: 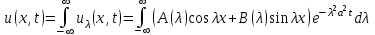 , ,
Неизвестные функции 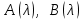 должны быть такими, чтобы выполнялось условие должны быть такими, чтобы выполнялось условие 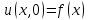 : : 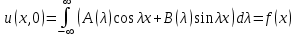
.
| 3-Билет
№
|
Вопросы/задания
|
1
|
Дайте определение скалярного поля. Введите основную характеристику скалярного поля.Запишите все формулы для вычисления градиента скалярного поля.
Если каждой точке пространства поставлено в соответствие определенное значение некоторой скалярной величины, то говорят, что в этом пространстве определено скалярное поле этой величины.
Основными характеристиками скалярного поля являются поверхности
(или линии) уровня, производная по направлению и градиент.
Поверхностью уровня скалярного поля называется множество точек этого поля, в которых функция u(M) принимает постоянное
значение, т.е. u(x;y;z) = C (C = const).
Если задано плоское скалярное поле u = u (x; y), то равенство
u (x;y) = C, определяет не поверхности, а линии уровня. Известные из
физики изотермы (линии равной температуры), изобары (линии равного давления), эквипотенциальные линии (линии равного потенциала) являются
примером линий уровня в различных плоских физических скалярных полях.
Градиент является основной характеристикой скалярного поля и обладает следующими свойствами:
1) 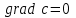 , где – постоянная; , где – постоянная;
2) 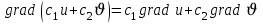 , где , где 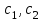 - постоянные; - постоянные;
3) 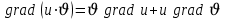 ; ;
4) 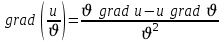 ; ;
5) 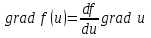 . .
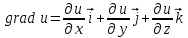 , , 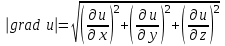
|
2
|
Рассмотрите специальные функции.Назовите цилиндрические функции. Запишите шаровые и сферические функции.Перечислите свойства функции Дирака.
Специальные функции : функция Бесселя , функция Неймана уравнение Бесселя и Лапласа
Интегралы этого уравнения называются цилиндрическими функциями или функциями Бесселя:
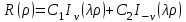 , ,
где 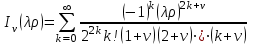 - бесселева функция первого рода порядка - бесселева функция первого рода порядка 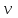 . .
Если 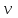 есть целое число ( есть целое число (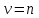 ), то решение уравнения Бесселя выражается формулой ), то решение уравнения Бесселя выражается формулой
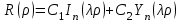 , ,
где 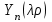 - функция Бесселя второго рода, которую еще называют функцией Неймана. - функция Бесселя второго рода, которую еще называют функцией Неймана.
Следовательно, конечными решениями уравнения (4.13) являются сферические функции:
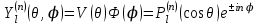 . .
Произведение радиальной функции 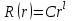 на любую сферическую функцию на любую сферическую функцию 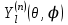 является частным ограниченным решением уравнения Лапласа: является частным ограниченным решением уравнения Лапласа:
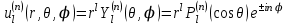 . .
Функции 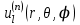 называют шаровыми. Общее решение уравнения Лапласа имеет вид: называют шаровыми. Общее решение уравнения Лапласа имеет вид: 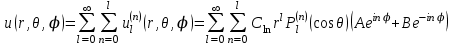
Дельта-функция Дирака определяется следующим образом: 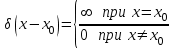
При этом
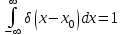
Основное свойство дельта-функции 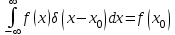
Его называют «фильтрующим» свойством данной функции.
Кроме того, функция Дирака обладает следующими свойствами:
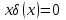
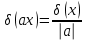
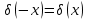
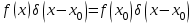
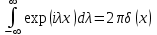
| |
 Скачать 3.75 Mb.
Скачать 3.75 Mb.