|
|
вавм. Билеты методы математический физики 2022 фипк-211. Дайте определение скалярного поля. Приведите примеры скалярного поля. Покажите как графически изображается скалярное поле. Приведите примеры.
17-Билет
№
|
|
1
|
Введите криволинейные координаты. Напишите уравнения, определяющие координатные поверхности. Дайте определение координатных линий. Запишите соотношения, доказывающие что криволинейная система координат является ортогональной. Выразите элементы длин дуг соответствующих координатных линий, элементы площадей координатных поверхностей и элемент объема при помощи коэффициентов Ламе.
Числа , определяющие положение точки в пространстве, называются криволинейными координатами. Так как радиус-вектор некоторой точки однозначно определяется ее прямоугольными координатами, то криволинейные координаты являются функциями декартовых координат этой точки:
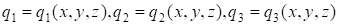
Уравнения 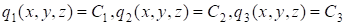 определяют поверхности уровня для скалярных функций определяют поверхности уровня для скалярных функций 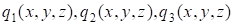
Пересечение двух координатных поверхностей называется координатной линией. Направления координатных линий задаются единичными базисными векторами (ортами)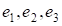 которые в каждой точке пространства направлены по касательным и координатным линиям в сторону возрастания переменных которые в каждой точке пространства направлены по касательным и координатным линиям в сторону возрастания переменных 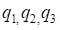
Система криволинейных координат называется ортогональной, если ее базисные векторы удовлетворяют следующим соотношениям:
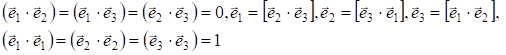
Величины 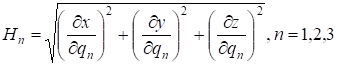 называются коэффициентами Ламе данной ортогональной криволинейной системы координат. Элементы длин дуг соответствующих координатных линий, элементы площадей координатных поверхностей и элемент объема выражаются при помощи коэффициентов Ламе следующим образом: называются коэффициентами Ламе данной ортогональной криволинейной системы координат. Элементы длин дуг соответствующих координатных линий, элементы площадей координатных поверхностей и элемент объема выражаются при помощи коэффициентов Ламе следующим образом:
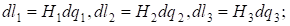 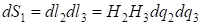
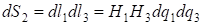 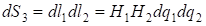
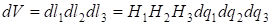
|
2
|
Приведите классификацию краевых задач. Дайте определение задачи Коши.
Краевые задачи:
Задача Дирихле. Найти функцию 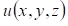 удовлетворяющую внутри области уравнению Лапласа удовлетворяющую внутри области уравнению Лапласа 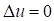 и на границе области краевому условию и на границе области краевому условию
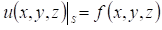
Где 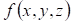 - известная функция, определенная на поверхности - известная функция, определенная на поверхности
Задача Неймана. Найти функцию 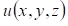 удовлетворяющую внутри области уравнению Лапласа удовлетворяющую внутри области уравнению Лапласа 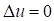 и на границе области краевому условию и на границе области краевому условию
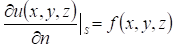
Где 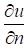 - нормальная производная функции - нормальная производная функции 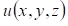 т. .е. производная, взятая в направлении внешней нормали к поверхности , т. .е. производная, взятая в направлении внешней нормали к поверхности ,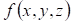 - известная функция, определенная на поверхности . - известная функция, определенная на поверхности .
3. Смешанная задача. Найти функцию 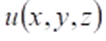 удовлетворяющую внутри области удовлетворяющую внутри области 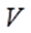 уравнению Лапласа уравнению Лапласа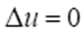 и на границе и на границе 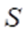 области краевому условию области краевому условию
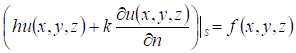
Где - некоторые постоянные,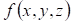 - известная функция, определенная на поверхности . - известная функция, определенная на поверхности .
Эти задачи соответственно называются первой, второй и третьей краевой задачей.

|
18-Билет
№
|
|
1
|
Запишите основные дифференциальные операции в криволинейных координатах. Приведите формулы для вычисления коэффициентов Ламе.
Основные дифференциальные операции в криволинейных координатах:
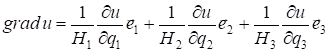
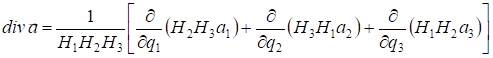
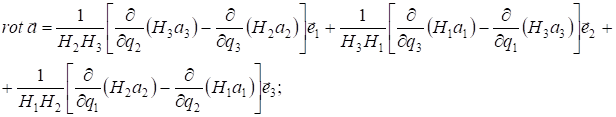
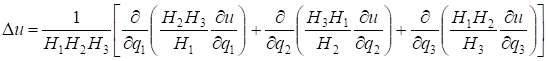
В цилиндрической системе координат с учетом коэффициентов Ламе выражаются формулами:
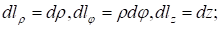 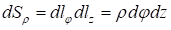
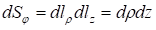 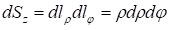
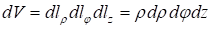
В сферической системе координат с учетом коэффициентов Ламе выражаются формулами:
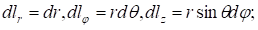
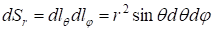
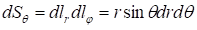
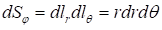
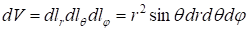
|
2
|
Напишите в чем заключается метод функции Грина. Приведите пример использования метода функции Грина.
Мы будем рассматривать 3 распространных методов:
1.Метод Фурье (разделение переменных)
2.Метод Даламбера(метод характеристик)
3.Метод функции Грина
Метод Фурье- с его помощью которого можно расщепить уравнение в частных производных для функции n независимых переменных на n обыкновенных дифференциальных уравнений.
Метод Даламбера-задача для уравнения колебаний струны.
Метод функции Грина-метод состоит в том, что сначала находят некоторое специальное решение задачи такого же типа, а затем через него в квадратурах выражают интеграл исходной задачи.
Метод функции Грина-метод состоит в том, что сначала находят некоторое специальное решение задачи того же типа, а затем через него в квадратурах выражают интеграл исходной задачи.
В качестве примера рассмотрим задачу из электростатики. Пусть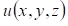 - потенциал электростатического поля, создаваемого во всем пространстве электрическими зарядами, распределенными с плотностью - потенциал электростатического поля, создаваемого во всем пространстве электрическими зарядами, распределенными с плотностью 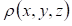 в заданном конечном объеме . В этом случае краевое условие имеет вид в заданном конечном объеме . В этом случае краевое условие имеет вид 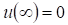 , а искомое решение удовлетворяет уравнению Пуассона: , а искомое решение удовлетворяет уравнению Пуассона:
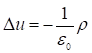
Поле полностью определяется распределением заряда , поэтому решение ищем в виде:
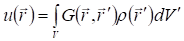
Где - решение задачи для точечного источника, т.е. поля, создаваемого точечным единичным зарядом. Распределение такого заряда выражается функцией:
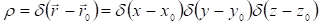
Где - точка, в которой находится заряд. Поэтому удовлетворяет уравнению:
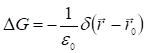
Функция Грина представляет собой потенциал электростатического поля в точке , создаваемый единичным точечным зарядом, помещенным в точку с радиусом-вектором . Следовательно, в рассматриваемом случае функцию Грина согласно знаниям из электростатики можем записать в виде
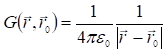
Тогда решение задачи для произвольного распределения заряда определяется по формуле:
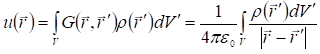
Эта формула имеет простой смысл: она выражает принцип суперпозиции.
|
19-Билет
№
|
|
1
|
Дайте определения скалярной, векторной и тензорной величины. Заполните таблицу. Приведите примеры не менее 2 физических величин каждого вида.
Скалярная величина-это величина, которая имеет только одну характеристику-численное значение.
Векторная величина- это величина, которая имеет величину и направление.
Тензором называется величина,характеризумая в системе координат Х Y Z двумя векторами.
№
|
Физическая величина
|
Укажите вид
|
Обозначение
|
Единица измерения
|
1
|
Масса
|
Скалярной
|
M
|
Кг
|
2
|
Время
|
Скалярной
|
T
|
С
|
3
|
Скорость
|
Векторной
|
V
|
м/с
|
4
|
Сила
|
Векторной
|
F
|
Н
|
5
|
Интервал
|
Тензорной
|
S
|
M
|
6
|
Форма обьема
|
Тензорной
|
N
|
|
Назовите физические задачи, описываемые уравнениями эллиптического типа. Перечислите методы решения уравнений эллиптического типа. С помощью одного из методов решите уравнение эллиптического типа.
уравнения Пуассона
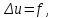 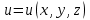
уравнение Лапласа
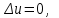 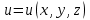
стационарное уравнение Шредингера
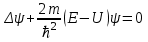
Для решения уравнений эллиптического типа можно использовать распространенные методы решения: метод разделения переменных, метод функции Грина.
Метод функции Грина состоит в том, что сначала находят некоторое специальное решение задачи такого же типа, а затем через него в квадратурах выражают интеграл исходной задачи.
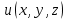 - потенциал электростатического поля, создаваемого во всем пространстве электрическими зарядами, распределенными с плотностью - потенциал электростатического поля, создаваемого во всем пространстве электрическими зарядами, распределенными с плотностью 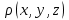 в заданном конечном объеме в заданном конечном объеме 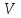 . В этом случае краевое условие имеет вид . В этом случае краевое условие имеет вид 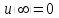 , а искомое решение удовлетворяет уравнению Пуассона , а искомое решение удовлетворяет уравнению Пуассона
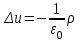 . .
Поле полностью определяется распределением заряда 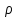 , поэтому решение ищем в виде , поэтому решение ищем в виде 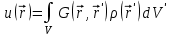 , ,
где 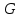 - решение задачи для точечного источника, т.е. поля, создаваемого точечным единичным зарядом. Распределение такого заряда выражается функцией - решение задачи для точечного источника, т.е. поля, создаваемого точечным единичным зарядом. Распределение такого заряда выражается функцией
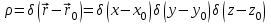 , ,
где 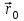 - точка, в которой находится заряд. Поэтому - точка, в которой находится заряд. Поэтому 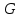 удовлетворяет уравнению удовлетворяет уравнению
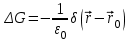 . .
Функция Грина представляет собой потенциал электростатического поля в точке 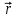 , создаваемый единичным точечным зарядом, помещенным в точку с радиусом-вектором , создаваемый единичным точечным зарядом, помещенным в точку с радиусом-вектором 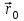 . .
|
2
| |
|
|
 Скачать 3.75 Mb.
Скачать 3.75 Mb.