вавм. Билеты методы математический физики 2022 фипк-211. Дайте определение скалярного поля. Приведите примеры скалярного поля. Покажите как графически изображается скалярное поле. Приведите примеры.
 Скачать 3.75 Mb. Скачать 3.75 Mb.
|
|
2.Во многих задачах физики применяются дифференциальные уравнения в частных производных второго порядка. Приведите не менее пяти наиболее часто вcтречающихся видов таких уравнений. Во многих задачах физики применяются дифференциальные уравнения в частных производных второго порядка нескольких наиболее часто встречающихся видов. При изучении волн различной физической природы – упругих, электромагнитных, волн плотности заряда в плазме и т.д. - применяется волновое уравнение 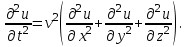 Здесь функция 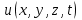 может быть давлением или плотностью для упругих волн в газах, напряженностью электрического или магнитного поля и т.д.; может быть давлением или плотностью для упругих волн в газах, напряженностью электрического или магнитного поля и т.д.; 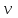 - скорость распространения волн в данной среде. - скорость распространения волн в данной среде.Распространение тепла в однородном изотропном теле, процессы диффузии описываются уравнением теплопроводности 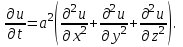 Здесь функция 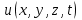 имеет смысл температуры или концентрации. имеет смысл температуры или концентрации.Установившееся тепловое состояние в однородном изотропном теле описывается уравнением Пуассона 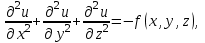 где функция 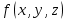 связана с плотностью источников тепла. связана с плотностью источников тепла. При отсутствии источников тепла внутри тела установившееся тепловое состояние описывается уравнением Лапласа 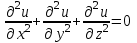 Уравнением Лапласа также описываются потенциалы поля тяготения и электростатического поля при отсутствии масс или зарядов. Основным уравнением квантовой механики является уравнение Шредингера, которое имеет вид 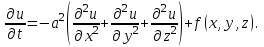 Здесь комплексная функция 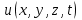 , называемая волновой функцией, определяет амплитуду вероятности обнаружения микрочастицы, а функция , называемая волновой функцией, определяет амплитуду вероятности обнаружения микрочастицы, а функция 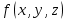 связана с потенциальной энергией микрочастицы во внешнем силовом поле. связана с потенциальной энергией микрочастицы во внешнем силовом поле. Приведенные уравнения называются основными уравнениями математической физики. 8-Билет 1.Дайте определение циркуляции векторного поля. Приведите инвариантное определение ротора векторного поля. Запишите формулу для вычисления ротора векторного поля в декартовых координатах. Приведите основные свойства ротора векторного поля. Сформулируйте теорему Стокса. Запишите математическое выражение этой теоремы. Циркуляцией векторного поля вдоль кривой называется линейный интеграл 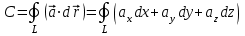 . .Физический смысл циркуляции в силовом поле состоит в том, что она равна работе по перемещению точки вдоль кривой в заданном направлении. Ротором векторного поля в точке 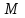 называется вектор, проекция которого на направление нормали называется вектор, проекция которого на направление нормали 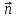 равна пределу отношения циркуляции векторного поля по контуру плоской площадки равна пределу отношения циркуляции векторного поля по контуру плоской площадки 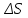 , перпендикулярной в точке , перпендикулярной в точке 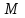 этому направлению этому направлению 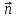 , к площадке , к площадке 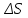 , когда размеры площадки стремятся к нулю, а сама площадка стягивается в точку: , когда размеры площадки стремятся к нулю, а сама площадка стягивается в точку: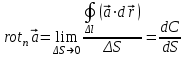 . .Ротор векторного поля есть векторная функция 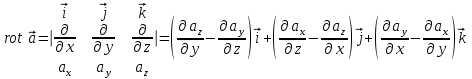 (1.8) (1.8)Ротор векторного поля обладает следующими свойствами: 1) 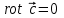 , , 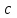 – постоянная; – постоянная;2) 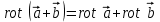 ; ;3) 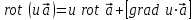 . .Ротор векторного поля характеризует вращательную способность векторного поля в данной точке. Векторное поле, ротор которого равен нулю, называется потенциальным. Циркуляция векторного поля по замкнутому контуру вычисляется по формуле: 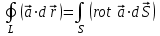 , , которая выражает теорему Стокса: циркуляция векторного поля по замкнутому контуру равна потоку ротора этого вектора через произвольную поверхность, опирающуюся на данный контур Вычислить циркуляцию векторного поля 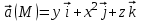 по контуру по контуру 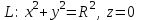 Для вычисления циркуляции векторного поля по заданному контуру воспользуемся теоремой Стокса. В качестве поверхности, натянутой на контур L, выберем круг, ограниченный указанной окружностью. При этом нормаль к поверхности должна совпадать с ортом 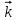 , что будет соответствовать положительному обходу контура L. , что будет соответствовать положительному обходу контура L. Согласно теореме Стокса (1.9) 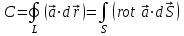 Вычислим ротор векторного поля 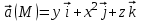 по формуле (1.8) по формуле (1.8) 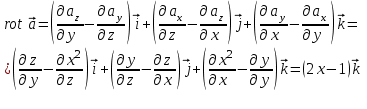 Подставив полученное значение ротора векторного поля в теорему Стокса, получим 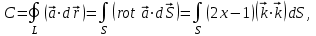 где 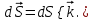 Перейдя к полярным координатам и учитывая, что 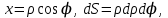 получим получим 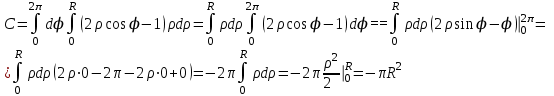 2.Запишите обобщенное и простое уравнение Лежандра. Изложите методику решения уравнения Лежандра. Запишите формулы Родриго для полиномов Лежандра. 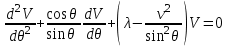 - обобщенные уравнения Лежандра. - обобщенные уравнения Лежандра.Если ввести новую независимую переменную 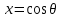 и обозначить и обозначить 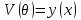 , то обобщенное уравнение Лежандра принимает обычный вид: , то обобщенное уравнение Лежандра принимает обычный вид: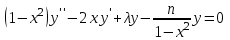 При 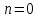 это уравнение имеет более простую форму уравнения Лежандра: это уравнение имеет более простую форму уравнения Лежандра: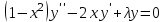 . .Интеграл обобщенным уравнением Лежандра имеет вид: 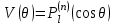 , , где 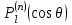 - присоединенные полиномы Лежандра, вычисляемые по формуле Родриго - присоединенные полиномы Лежандра, вычисляемые по формуле Родриго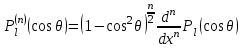 . .Здесь 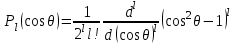 - полиномы Лежандра. - полиномы Лежандра.Обобщенное уравнение Лежандра 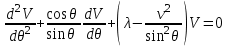 . . 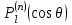 - присоединенные полиномы Лежандра, вычисляемые по формуле Родриго - присоединенные полиномы Лежандра, вычисляемые по формуле Родриго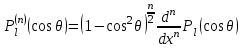 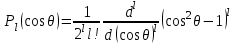 - полиномы Лежандра.. - полиномы Лежандра..  9-Билет 1.Дайте определение векторного поля. Приведите классификацию векторных полей. Напишите условие соленоидальности, условие потенциальности векторного поля. Дайте определение гармонического векторного поля. Напишите формулу, выражающую условие гармоничности векторного поля. Векторное поле— это отображение, которое каждой точке рассматриваемого пространства ставит в соответствие вектор с началом в этой точке. Классификация векторных полей: соленоидальнос diva(вектор)=0, потенциальное rotа(вектор)=0. Потенциальное соленоидальное поле называется гармоническим (лапласовым). div𝑎 𝑀 = 0, rot𝑎 𝑀 = 0 Cкалярный потенциал несжимаемого потенциального поля удовлетворяет уравнению Лапласа: ∆𝑢 = 0  2.Введите основные понятия и определения теории дифференциального уравнения в частных производных. Приведите классификацию дифференциальных уравнений в частных производных. Напишите формулу, выражающую общий вид линейного дифференциального уравнения в частных производных второго порядка. Дифференциальное уравнение, содержащее, кроме независимых переменных и искомой функции, частные производные этой функции, называется дифференциальным уравнением с частными производными. Наивысший порядок входящих в уравнение частных производных называется порядком дифференциального уравнения. Для математической физики наиболее важны и лучше всего изучены уравнения второго порядка. В случае двух независимых переменных уравнение второго порядка может быть записано в следующей общей форме: Решением (интегралом)дифференциального уравнения в частных производных называется функция, которая, будучи подставленной в уравнение вместо искомой функции и ее частных производных, обращает это уравнение в тождество по всем независимым переменным в рассматриваемой области. Уравнение является линейным,если все производные и сама неизвестная функция входят в это уравнение в первой степени. Процесс нахождения всех решений дифференциального уравнения в частных производных называется интегрированиемэтого уравнения. Общее решение дифференциального уравнения в частных производных зависит от произвольных функций, число которых равно порядку этого уравнения. Любое решение дифференциального уравнения в частных производных, входящих в состав общего решения, называется частным решениемэтого уравнения. Для того чтобы найти интересующее нас решение дифференциального уравнения в частных производных, надо присоединить к уравнению некоторые дополнительные условия, которым оно удовлетворяет. Дополнительные условия делятся на начальные и граничные (краевые). К  лассификация дифференциальных уравнений в частных производных: линейные и нелинейные; однородные и неоднородные; с постоянными коэффициентами и с переменными коэффициентами Уравнение называется линейным, если оно линейно относительно искомой функции и всех ее производных. Линейное уравнение 2-го порядка с двумя независимыми переменными имеет следующий общий вид: 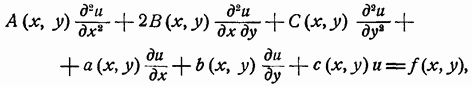 где некоторые заданные функции переменных х, у. Уравнение с частными производными второго порядка называется линейным относительно старших производных, если оно содержит эти производные лишь в первой степени. 10-Билет
|

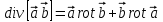 , используя непосредственное вычисление.
, используя непосредственное вычисление. 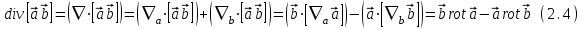
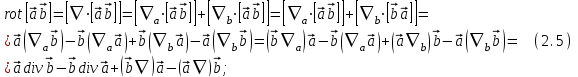
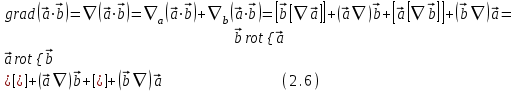
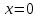 и
и 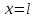
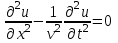 ,
, 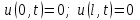
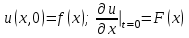 .
.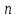
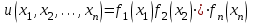 .
.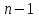 произвольных
произвольных 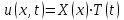 .
.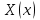 и
и 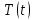 получим обыкновенные дифференциальные уравнения
получим обыкновенные дифференциальные уравнения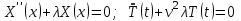 ,
,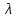 - параметр разделения. При
- параметр разделения. При 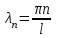 существуют нетривиальные решения уравнения, удовлетворяющие краевым условиям, и ими являются функции
существуют нетривиальные решения уравнения, удовлетворяющие краевым условиям, и ими являются функции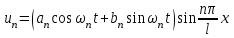 ,
, 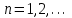 ,
, 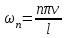 .
.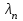 называются собственными значениями, а соответствующие им функции – собственными функциями задачи.
называются собственными значениями, а соответствующие им функции – собственными функциями задачи.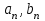 , при которых выполняются начальные условия.
, при которых выполняются начальные условия.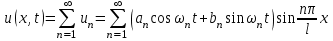 ,
, 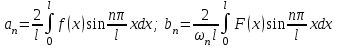 .
.