|
|
вавм. Билеты методы математический физики 2022 фипк-211. Дайте определение скалярного поля. Приведите примеры скалярного поля. Покажите как графически изображается скалярное поле. Приведите примеры.
15-Билет
№
|
|
1
|
Назовите сферические координаты. Покажите связь сферических и декартовых координат. Сделайте рисунок и покажите координатные поверхности и координатные линии в сферической системе координат. Определите коэффициенты Ламе в сферической системе координат и выразите элементы длин дуг соответствующих координатных линий, элементы площадей координатных поверхностей и элемент объема при помощи этих коэффициентов. Запишите основные дифференциальные операции в сферических координатах.
В сферической системе координат положение точки 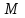 пространства определяется тремя величинами: расстоянием пространства определяется тремя величинами: расстоянием 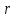 от точки от точки 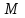 до фиксированной точки до фиксированной точки 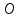 ; углом ; углом 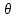 , образованным радиус-вектором точки , образованным радиус-вектором точки 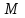 и фиксированной полупрямой и фиксированной полупрямой 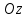 ; углом ; углом 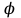 , образованным фиксированной плоскостью , образованным фиксированной плоскостью  и полуплоскостью, ограниченной осью и полуплоскостью, ограниченной осью  и проходящей через точку и проходящей через точку  . В сферической системе координат . В сферической системе координат 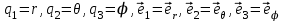 , причем , причем 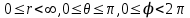
Связь декартовых координат точки с ее сферическими координатами выражается соотношениями 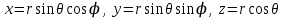
*Рисунок*
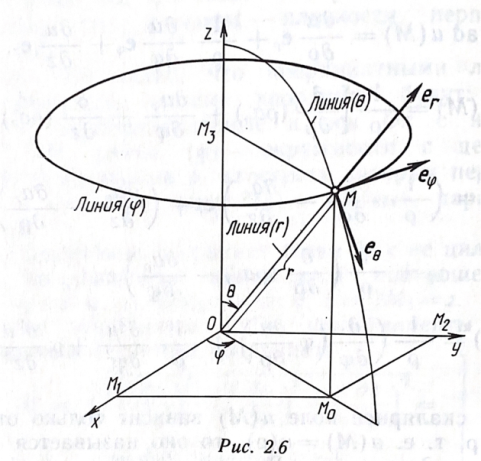
Координатными поверхностями в случае сферической системы координат являются: 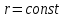 – сферы с центрами в точке – сферы с центрами в точке 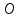 ; ; 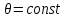 – конусы с осью – конусы с осью 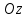 ; ; 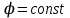 – полуплоскости, ограниченные осью – полуплоскости, ограниченные осью 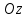 . .
Координатными линиями будут: линии 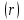 – лучи, выходящие из центра – лучи, выходящие из центра 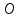 ; линии ; линии 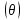 – окружности (меридианы) с центрами в точке – окружности (меридианы) с центрами в точке 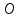 и радиусами и радиусами 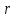 , пересекающие ось , пересекающие ось 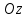 ; линии ; линии 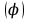 – окружности (параллели) с центрами на оси – окружности (параллели) с центрами на оси 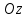 и радиусами и радиусами 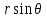 . .
Коэффициенты Ламе в сферической системе координат определяются следующим образом:
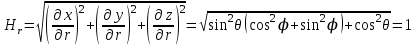 , ,
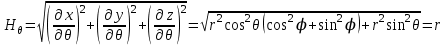
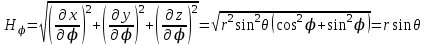 . .
Элементы длин дуг соответствующих координатных линий, элементы площадей координатных поверхностей и элемент объема в сферической системе координат с учетом коэффициентов Ламе выражаются формулами:
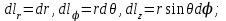
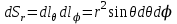 , ,
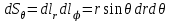 , ,
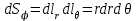 , ,
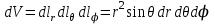 . .
Для основных дифференциальных операций в сферической системе координат получаются следующие выражения:
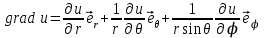 ; ;
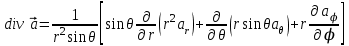 ; ;
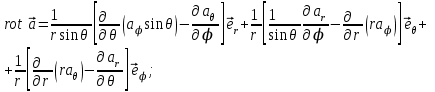
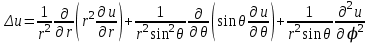 . .
|
2
|
Назовите физические задачи, описываемые уравнениями гиперболического типа. Перечислите методы решения уравнений гиперболического типа. С помощью одного из методов решите уравнение данного типа.
Физические задачи, описываемые уравнениями гиперболического типа: Волновые уравнения, Колебание струны .
Методы решения уравнений гиперболического типа:Метод характеристик – метод Даламбера. Метод разделения переменных-Метод Фурье.
Применим метод Даламбера для уравнения гиперболического типа.
Рассмотрим бесконечно длинную однородную струну, на которую среда никакого сопротивления не оказывает и никакие внешние силы на струну не действуют. Задача о колебаниях такой струны сводится к отысканию решений уравнения
 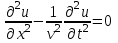
при заданных начальных условиях
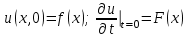 . .
Это задача Коши. Решим методом характеристик (методом Даламбера).
Сначала производят замену переменных: 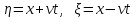 . .
 
 
Таким образом, всякое решение уравнения 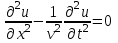 является суперпозицией двух произвольных волн, распространяющихся в противоположных направлениях. Вид функций является суперпозицией двух произвольных волн, распространяющихся в противоположных направлениях. Вид функций 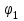 и и 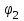 в каждом конкретном случае определяется начальными условиями. Если в каждом конкретном случае определяется начальными условиями. Если 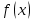 и и 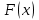 – соответственно дважды и один раз дифференцируемые функции, то решение рассматриваемой задачи задается формулой – соответственно дважды и один раз дифференцируемые функции, то решение рассматриваемой задачи задается формулой
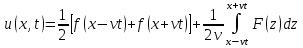 . .
Эта формула называется формулой Даламбера.
Если 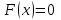 , то решение задачи Коши определяется формулой , то решение задачи Коши определяется формулой
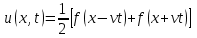 . .
Оно является суперпозицией прямой 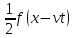 и обратной и обратной 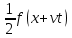 волн. Процесс, описываемый этим уравнением, называется распространением волн отклонения. волн. Процесс, описываемый этим уравнением, называется распространением волн отклонения.
Если 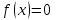 , то решение задачи Коши определяется формулой , то решение задачи Коши определяется формулой
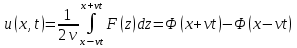 . .
|
16-Билет
№
|
Вопросы/задания
|
1
|
Дайте определение векторных линий. Приведите примеры векторных линий. Выведите формулу, выражающую уравнение векторных линий.
Векторной линией векторного поля ā(M)
называется линия, в каждой точке которой направление
касательной совпадает с направлением поля (т.е. с вектором
ā(M) )
ПРИМЕРЫ:
1)В поле скоростей текущей жидкости векторные линии – линии тока жидкости.
2)В электрическом (электромагнитном) поле векторные линии –
силовые линии.
В векторном поле ā= P(x;y;z)i+ Q(x;y;z)j+ R(x;y;z)k векторные
линии – решение системы дифференциальных уравнений
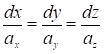
Найти векторные линии векторного поля 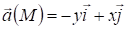
Уравнения векторных линий имеют вид:
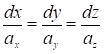
Для данного случая получим:
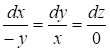
Отсюда следует, что 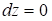 и и 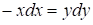 . Интегрируем полученные дифференциальные уравнения и получим: . Интегрируем полученные дифференциальные уравнения и получим:
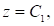 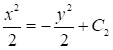
Первое уравнение задает плоскости, параллельные плоскости  а второе – семейство окружностей а второе – семейство окружностей 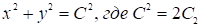
Таким образом, векторные линии рассматриваемого векторного поля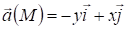 представляют собой концентрические окружности радиусом с центром на оси на оси лежащие в плоскости представляют собой концентрические окружности радиусом с центром на оси на оси лежащие в плоскости
|
2
|
Запишите линейное однородное дифференциальное уравнение второго порядка. Допустите, что искомая функция зависит от двух переменных. Составьте характеристическое уравнение и приведите дифференциальное уравнение к каноническому виду.
Наиболее часто в физике используются дифференциальные уравнения в частных производных второго порядка.
Если искомая функция зависит только от двух независимых переменных, то такое уравнение примет вид:
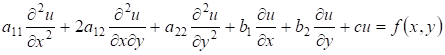 (3.1) (3.1)
В данном уравнении если 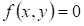 , то уравнение называется однородным. , то уравнение называется однородным.
Для того чтобы привести дифференциальное уравнение в частных производных к каноническому виду, надо составить его характеристическое уравнение:
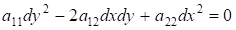 (3.2) (3.2)
которое распадается на два уравнения:
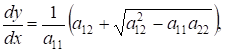 (3.3) (3.3)
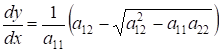 (3.4) (3.4)
и найти их общие интегралы.
Интегральные кривые уравнения (3.2) или, что то же самое, уравнений (3.3) и (3.4), называются характеристиками уравнения (3.1).
Если уравнение (3.1) гиперболического типа, то интегралы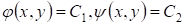 уравнений (3.3) и (3.4) вещественны и различны. Они определяют два различных семейства вещественных характеристик уравнения (3.1). С помощью замены переменных уравнений (3.3) и (3.4) вещественны и различны. Они определяют два различных семейства вещественных характеристик уравнения (3.1). С помощью замены переменных 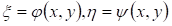 уравнение (3.1) приводят к каноническому виду уравнения гиперболического типа: уравнение (3.1) приводят к каноническому виду уравнения гиперболического типа:
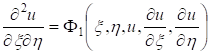
Если же уравнение (1) параболического типа, то уравнения (3.3) и (3.4) совпадают, и мы получаем один общий интеграл характеристического уравнения (3.2): 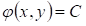 , определяющий одно семейство вещественных характеристик уравнения (3.1). Произведя замену переменных по формулам , определяющий одно семейство вещественных характеристик уравнения (3.1). Произведя замену переменных по формулам 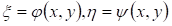 , где , где 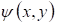 — такая функция, что — такая функция, что 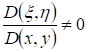 в рассматриваемой области, приведем уравнение (3.1) к виду: в рассматриваемой области, приведем уравнение (3.1) к виду:
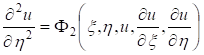
называемому каноническим видом уравнения параболического типа.
Наконец, если уравнение (3.1) эллиптического типа, то общие интегралы уравнений (3.3) и (3.4) комплексно-сопряженные:
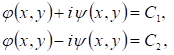
где 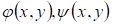 - вещественные функции, определяющие два семейства мнимых характеристик уравнения (3.1). Произведя замену переменных по формулам - вещественные функции, определяющие два семейства мнимых характеристик уравнения (3.1). Произведя замену переменных по формулам 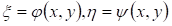 , приведем уравнение (3.1) к виду: , приведем уравнение (3.1) к виду:
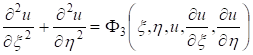
называемому каноническим видом уравнения эллиптического типа.
| |
|
|
 Скачать 3.75 Mb.
Скачать 3.75 Mb.