|
|
вавм. Билеты методы математический физики 2022 фипк-211. Дайте определение скалярного поля. Приведите примеры скалярного поля. Покажите как графически изображается скалярное поле. Приведите примеры.
11-Билет
№
|
Вопросы/задания
|
1
|
Назовите дифференциальные операции второго порядка. Используя оператор Гамильтона, найдите выражения для дифференциальных операций второго порядка. Составьте таблицу дифференциальных операций второго порядка. Запишите выражение оператора Лапласа в декартовых координатах.
Ротор градиента скалярного поля 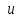
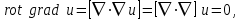
Дивергенция ротора векторного поля 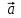
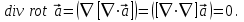
Ротор ротора векторного поля 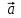
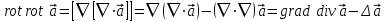
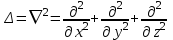 - оператор Лапласа или лапласиан. - оператор Лапласа или лапласиан.
|
2
|
Дайте определение дифференциального уравнения в частных производных. Назовите типы дифференциальных уравнений в частных производных. Приведите их примеры. Покажите как определять тип дифференциального уравнения в частных производных.
Уравнение,связывающее искомую функцию,независимые переменные и частные производные искомой функции по этим независимым переменным,называется дифференциальным уравнением в частных производных.
Параболический тип
Гиперболический тип
Эллиптический тип
К уравнениям гиперболического типа относятся:
трехмерное волновое уравнение
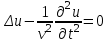 , где , где 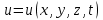 , ,
одномерное волновое уравнение (уравнение колебаний струны)
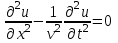 , где , где 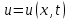 , ,
неоднородное волновое уравнение (уравнение Даламбера)
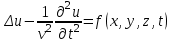 . .
Уравнения параболического типа получаются при исследовании таких физических явлений, как теплопроводность, диффузия, распространение электромагнитных полей в проводящих средах, движение вязкой жидкости. К уравнениям параболического типа относятся уравнения теплопроводности, уравнения диффузии. Они могут быть одномерными, двумерными или трехмерными, однородными или неоднородными.
Одномерная задача о распределении температуры в стержне приводится к исследованию уравнения теплопроводности, которое в общем виде может быть представлено в виде:
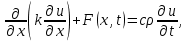
К уравнениям эллиптического типа относятся:
уравнения Пуассона
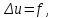 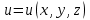
уравнение Лапласа
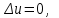 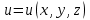
стационарное уравнение Шредингера
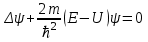
В зависимости от значения коэффициентов, стоящих при старших производных, уравнения подразделяются на несколько типов. Если 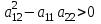 , то дифференциальное уравнение в частных производных называется уравнением гиперболического типа; если , то дифференциальное уравнение в частных производных называется уравнением гиперболического типа; если 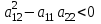 , то – уравнением эллиптического типа; если , то – уравнением эллиптического типа; если 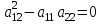 , то – уравнением параболического типа. , то – уравнением параболического типа.
|
12-Билет
№
|
Вопросы/задания
|
1
|
Дайте инвариантное определение дивергенции векторного поля. Приведите основные свойства дивергенции векторного поля. Запишите формулу, по которой вычисляется дивергенция векторного поля в декартовых координатах.
Потоком векторного поля 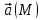 через бесконечно малую площадку через бесконечно малую площадку 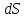 называется величина называется величина
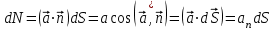 , ,
где 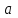 - значение векторного поля на площадке - значение векторного поля на площадке 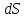 ; ; 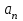 - проекция вектора - проекция вектора 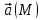 на направление положительной нормали. на направление положительной нормали.
Поток векторного поля 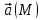 через замкнутую поверхность через замкнутую поверхность 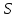
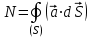 . .
Основными характеристиками векторного поля являются дивергенция и ротор. Дивергенцией векторного поля в данной точке называется предел, к которому стремится отношение потока векторного поля через произвольную, окружающую данную точку, поверхность к ограниченному этой поверхностью объему при стремлении последнего к нулю:
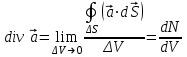 . .
Дивергенция векторного поля обладает следующими свойствами:
1) 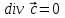 , , 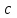 – постоянная; – постоянная;
2) 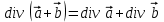 ; ;
3) 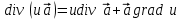 . .
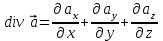 ; ;
|
2
|
Рассмотрите задачу о колебаниях бесконечно длинной струны. Приведите постановку задачи и найдите решение этого уравнения методом Даламбера.
Рассмотрим бесконечно длинную однородную струну, на которую среда никакого сопротивления не оказывает и никакие внешние силы на струну не действуют. Задача о колебаниях такой струны сводится к отысканию решений уравнения
 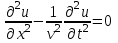
при заданных начальных условиях
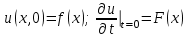 . .
Это задача Коши. Ее решают методом характеристик (методом Даламбера).
Сначала производят замену переменных: 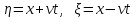 . .
В новых переменных исходное уравнение принимает вид: 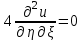 . .
Решение этого уравнения равно 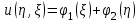
или, переходя к прежним переменным, 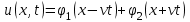 . .
Функция 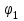 принимает одинаковые значения в тех точках, где аргумент функции фиксирован, т.е. принимает одинаковые значения в тех точках, где аргумент функции фиксирован, т.е. 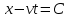 или или 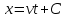 . Отсюда видно, что точка, в которой функция . Отсюда видно, что точка, в которой функция 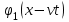 имеет заданное значение, перемещается со скоростью имеет заданное значение, перемещается со скоростью 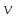 в положительном направлении оси в положительном направлении оси 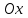 . Другими словами, функция . Другими словами, функция 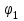 описывает некоторую волну, распространяющуюся вправо со скоростью описывает некоторую волну, распространяющуюся вправо со скоростью 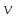 . Аналогично функция . Аналогично функция 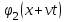 описывает волну, распространяющуюся влево с той же скоростью описывает волну, распространяющуюся влево с той же скоростью 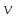 . .
Таким образом, всякое решение уравнения 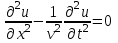 является суперпозицией двух произвольных волн, распространяющихся в противоположных направлениях. Вид функций является суперпозицией двух произвольных волн, распространяющихся в противоположных направлениях. Вид функций 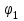 и и 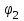 в каждом конкретном случае определяется начальными условиями. Если в каждом конкретном случае определяется начальными условиями. Если 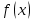 и и 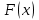 – соответственно дважды и один раз дифференцируемые функции, то решение рассматриваемой задачи задается формулой – соответственно дважды и один раз дифференцируемые функции, то решение рассматриваемой задачи задается формулой
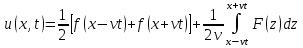 . .
Эта формула называется формулой Даламбера.
Если 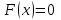 , то решение задачи Коши определяется формулой , то решение задачи Коши определяется формулой
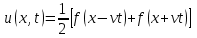 . .
Оно является суперпозицией прямой 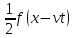 и обратной и обратной 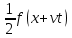 волн. Процесс, описываемый этим уравнением, называется распространением волн отклонения. волн. Процесс, описываемый этим уравнением, называется распространением волн отклонения.
Если 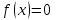 , то решение задачи Коши определяется формулой , то решение задачи Коши определяется формулой
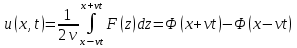 , ,
где 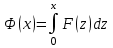 . Это решение является суперпозицией прямой . Это решение является суперпозицией прямой 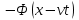 и обратной и обратной 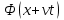 волн. Процесс, описываемый этим равенством, называется распространением волн импульса. волн. Процесс, описываемый этим равенством, называется распространением волн импульса.
| |
|
|
 Скачать 3.75 Mb.
Скачать 3.75 Mb.