Билет
№
|
Вопросы/задания
|
1
|
Дайте определение векторного поля. Приведите примеры векторного поля. Покажите как графически изображается векторное поле. Приведите примеры. Выведите формулу векторных линий.
Если каждой точке пространства сопоставлено определенное значение некоторой векторной величины, то говорят, что в этом пространстве определено векторное поле этой величины. Векторное поле можно рассматривать как вектор-функцию 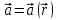 радиус-вектора точки или как вектор-функцию трех скалярных переменных радиус-вектора точки или как вектор-функцию трех скалярных переменных 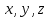 : :
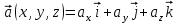 . .
Примером векторного поля является поле вектора 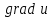 , которое определено в каждой точке пространства, если известно скалярное поле , которое определено в каждой точке пространства, если известно скалярное поле 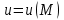 . .
Примерами векторного поля являются поля скорости и ускорения в текущей жидкости или газе, поле силы гравитации, поле интенсивности электростатического поля и тому подобные. Вообще, примером векторного поля может служить поле сил любой природы.
 Графическое изображение векторного поля Графическое изображение векторного поля
Векторное поле графически изображает при помощи векторных линий. Векторной линией векторного поля называется кривая, в каждой точке которой касательная совпадает с направлением поля в этой точке.
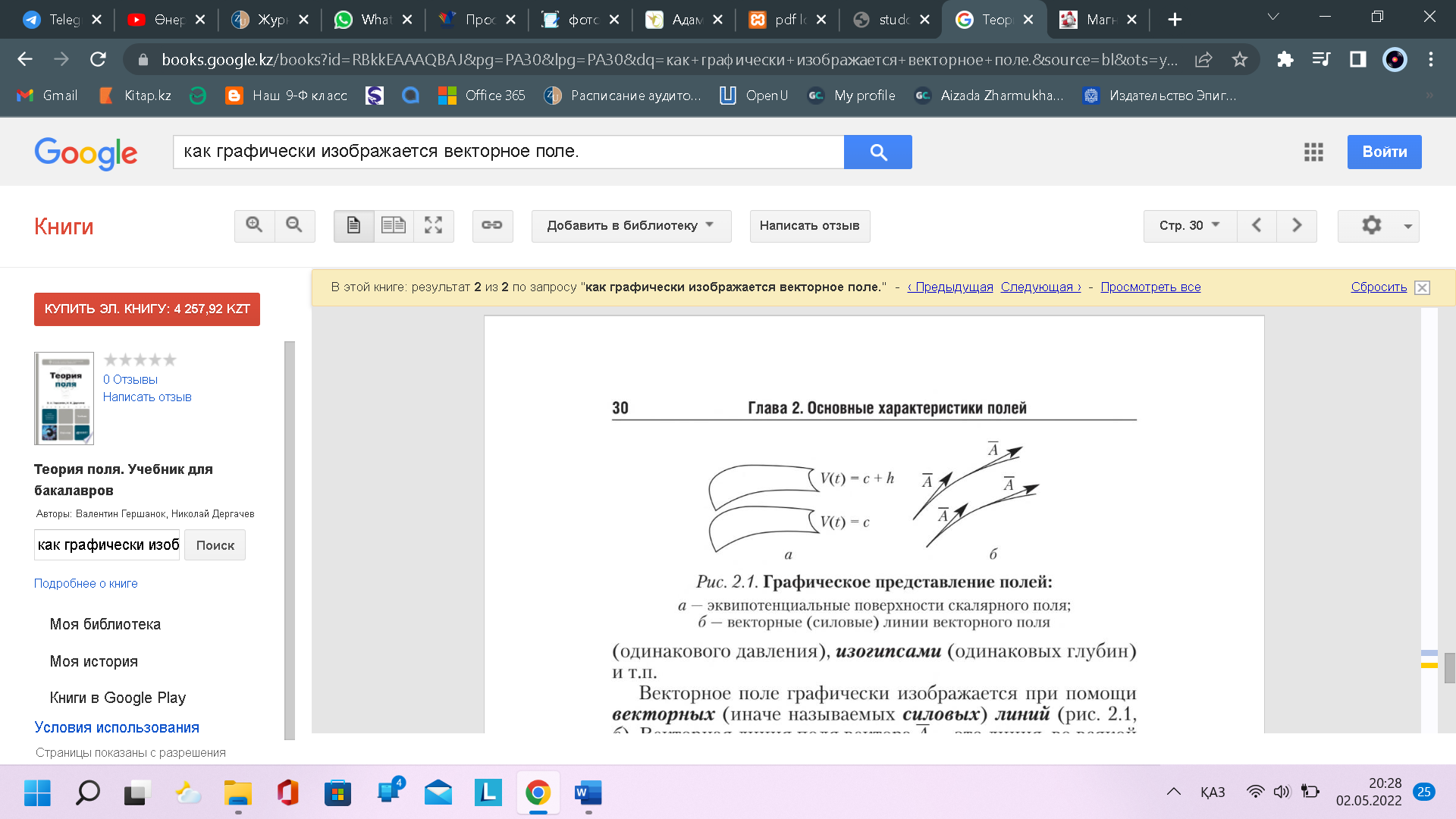 Векторные линии веторного поля Векторные линии веторного поля
Уравнения векторных линий векторного поля находят из системы дифференциальных уравнений
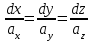 . .
Векторные линии силового поля называют обычно силовыми линиями, а векторные линии поля скоростей текущей жидкости – линиями тока. Примером силовых линий являются линии напряженности электрического поля.
|
2
|
Запишите уравнение Лапласа в сферических координатах. Найдите решение этого уравнения методом Фурье. Назовите специальные функции, которые встречаются при решении данного уравнения.
Уравнение Лапласа в сферических координатах имеет следующий вид:
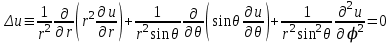 . (4.10) . (4.10)
Используя метод Фурье, ищем решение этого уравнения в виде произведения
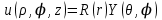 . (4.11) . (4.11)
Для функций 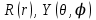 получим уравнения получим уравнения
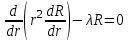 , (4.12) , (4.12)
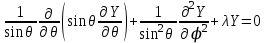 . (4.13) . (4.13)
Последнее уравнение – уравнение в частных производных. К нему еще раз применяем метод Фурье:
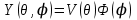 . (4.14) . (4.14)
Тогда получим уравнения
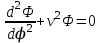 , (4.15) , (4.15)
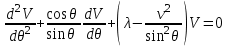 . (4.16) . (4.16)
Решение уравнения (4.15) в показательной форме выражается формулой
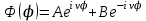 . .
Так как функция 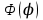 удовлетворяет условию цикличности удовлетворяет условию цикличности 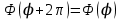 , то значение , то значение 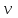 не может быть произвольным, а обязательно является целочисленным: не может быть произвольным, а обязательно является целочисленным: 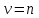 . Уравнение (4.16) называют обобщенным уравнением Лежандра. . Уравнение (4.16) называют обобщенным уравнением Лежандра.
Если ввести новую независимую переменную 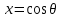 и обозначить и обозначить 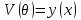 , то обобщенное уравнение Лежандра принимает обычный вид: , то обобщенное уравнение Лежандра принимает обычный вид:
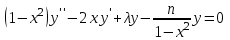
При 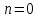 это уравнение имеет более простую форму уравнения Лежандра: это уравнение имеет более простую форму уравнения Лежандра: 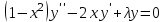 . .
Интеграл уравнения (4.16) имеет вид:
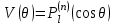 , ,
где 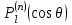 - присоединенные полиномы Лежандра, вычисляемые по формуле Родриго - присоединенные полиномы Лежандра, вычисляемые по формуле Родриго
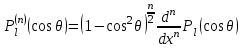 . .
Здесь 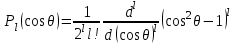 - полиномы Лежандра. - полиномы Лежандра.
Решение уравнения (4.12) имеет вид 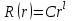 . .
Следовательно, конечными решениями уравнения (4.13) являются сферические функции:
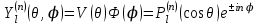 . .
Произведение радиальной функции 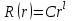 на любую сферическую функцию на любую сферическую функцию 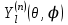 является частным ограниченным решением уравнения Лапласа: является частным ограниченным решением уравнения Лапласа:
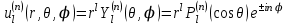 . .
Функции 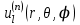 называют шаровыми. Общее решение уравнения Лапласа имеет вид: называют шаровыми. Общее решение уравнения Лапласа имеет вид:
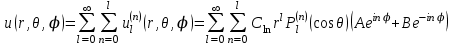 . .
|
5-Билет
№
|
Вопросы/задания
|
1
|
Дайте определение векторного поля. Введите основные характеристики скалярного поля. Запишите все формулы для вычисления основных характеристик векторного поля.
Если каждой точке пространства сопоставлено определенное значение некоторой векторной величины, то говорят, что в этом пространстве определено векторное поле этой величины. Векторное поле можно рассматривать как вектор-функцию 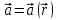 радиус-вектора точки или как вектор-функцию трех скалярных переменных радиус-вектора точки или как вектор-функцию трех скалярных переменных 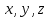 : :
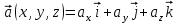 . .
Основными характеристиками скалярного поля являются: поверхности (линии) уровня, производная по направлению и градиент.
Градиент является основной характеристикой скалярного поля и обладает следующими свойствами: 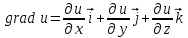
1) 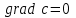 , где , где 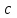 – постоянная; – постоянная;
2) 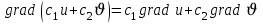 , где , где 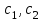 - постоянные; - постоянные;
3) 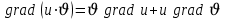 ; ;
4) 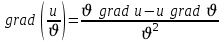 ; ;
5) 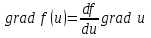 . .
Основными характеристиками векторного поля являются дивергенция и ротор.
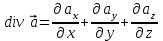 ; ;
Дивергенция векторного поля обладает следующими свойствами:
1) 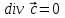 , , 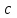 – постоянная; – постоянная;
2) 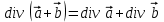 ; ;
3) 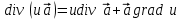 . .
|
2
|
Перечислите известные Вам методы решения дифференциальных уравнений в частных производных. Изложите суть каждого из перечисленных методов.
Существуют различные методы решения уравнений. К классическим часто употребляемым методам относятся метод характеристик (метод даламбера), метод разделения переменных(метод Фурье), метод функции Грина и другие.
Метод характеристик — метод решения дифференциальных уравнений в частных производных. Обычно применяется к решению уравнений в частных производных первого порядка, но он может быть применен и к решению гиперболических уравнений более высокого порядка. Метод заключается в приведении уравнения в частных производных к семейству обыкновенных дифференциальных уравнений.
Метод разделения переменных применим не всегда, но в тех случаях, когда им можно воспользоваться, является простейшим. С его помощью можно расщепить уравнение в частных производных для функции n независимых переменных на n обыкновенных дифференциальных уравнений.
Применим метод функции Грина для нахождения решений уравнений эллиптического типа. Метод функции Грина состоит в том, что сначала находят некоторое специальное решение задачи такого же типа, а затем через него в квадратурах выражают интеграл исходной задачи.
|
6-Билет
№
|
Вопросы/задания
|
1
|
Покажите как определяется поток векторного поля через элементарную поверхность и через полную замкнутую поверхность. Сформулируйте теорему Остроградского-Гаусса. Запишите математическое выражение этой теоремы. Приведите пример определения потока векторного поля с помощью теоремы Остроградского-Гаусса.
Потоком векторного поля 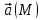 через бесконечно малую площадку через бесконечно малую площадку 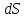 называется величина называется величина
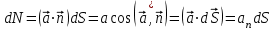 , ,
где 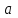 - значение векторного поля на площадке - значение векторного поля на площадке 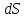 ; ; 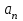 - проекция вектора - проекция вектора 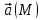 на направление положительной нормали. на направление положительной нормали.
Поток векторного поля 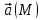 через замкнутую поверхность через замкнутую поверхность 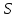
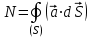 . .
Поток векторного поля через произвольную замкнутую поверхность вычисляется по формуле:
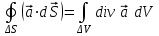 . (1.7) . (1.7)
Это соотношение выражает теорему Остроградского-Гаусса: поток векторного поля через произвольную замкнутую поверхность равен тройному интегралу от дивергенции, взятому по объему, ограниченному этой поверхностью.
|
2
|
Запишите уравнение Бесселя. Изложите методику решения уравнения Бесселя. Назовите цилиндрические функции. Запишите выражения для цилиндрических функций.
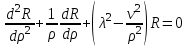
Это уравнение называется уравнением Бесселя. Интегралы этого уравнения называются цилиндрическими функциями или функциями Бесселя:
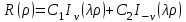 , ,
где 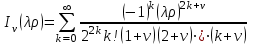 - бесселева функция первого рода порядка - бесселева функция первого рода порядка 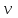 . .
Если 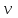 есть целое число ( есть целое число (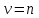 ), то решение уравнения Бесселя выражается формулой ), то решение уравнения Бесселя выражается формулой
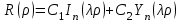 , ,
где 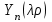 - функция Бесселя второго рода, которую еще называют функцией Неймана. - функция Бесселя второго рода, которую еще называют функцией Неймана.
Всякое решение уравнения Бесселя называется цилиндрической функцией.
Цилиндри́ческие фу́нкции — общее название для специальных функций одного переменного, являющихся решениями обыкновенных дифференциальных уравнений, получающихся при применении метода разделения переменных для уравнений математической физики, таких как уравнение Лапласа, уравнение Пуассона и др. в цилиндрической системе координат.
Наиболее часто встречающиеся цилиндрические функции:
Функции Бесселя
первого рода, ограниченные
второго рода (называемые также «функции Неймана»), неограниченные в нуле
Цилиндрическими функциями называются решения линейного дифференциального уравнения второго порядка:
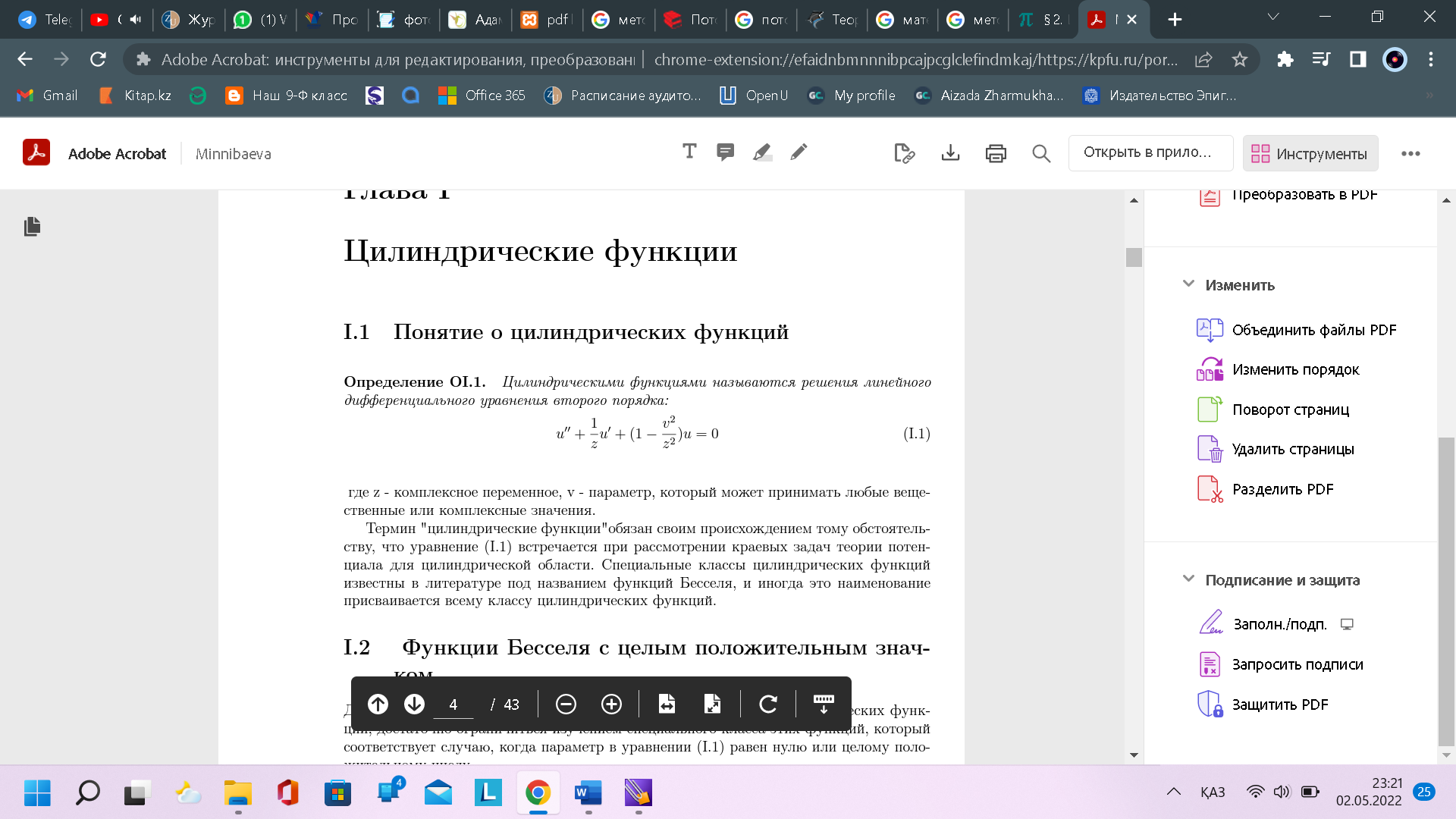
где z- комплексное переменное, v- параметр, который может принимать любые вещественные или комплексные значения. Термин "цилиндрические функции"обязан своим происхождением тому обстоятельству, что уравнение (I.1) встречается при рассмотрении краевых задач теории потенциала для цилиндрической области. Специальные классы цилиндрических функций известны в литературе под названием функций Бесселя, и иногда это наименование присваивается всему классу цилиндрических функций.
|
7-Билет
1.Запишите выражение для оператора Гамильтона. Назовите дифференциальные операции первого порядка. Выразите их с помощью оператора Гамильтона. Найдите результат действия оператора Гамильтона на произведения скалярных и векторных полей.
Дифференциальные операции могут быть записаны с помощью символического дифференциального оператора, введенного ирландским математиком У.Р. Гамильтоном. Оператор Гамильтона обозначается символом 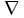 (читается «набла»; набла – древний музыкальный инструмент треугольной формы) и в декартовой системе координат имеет вид (читается «набла»; набла – древний музыкальный инструмент треугольной формы) и в декартовой системе координат имеет вид
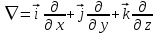 . .
Оператор Гамильтона действует на скалярные и векторные величины, находящиеся справа от него и формально подчиняется правилам дифференцирования и правилам векторной алгебры.
Дифференциальные операции первого порядка сводятся к следующим формулам:
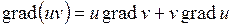 , ,
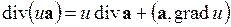 , ,
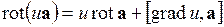 , ,
Результат действия оператора Гамильтона на произведения скалярных и векторных полей следующий:
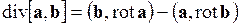 , ,
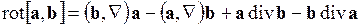 , ,
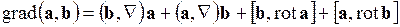 . .
Действие оператора Гамильтона на скалярное поле 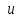 порождает векторное поле порождает векторное поле 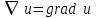 . Если повторно применить оператор . Если повторно применить оператор 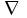 к векторному полю к векторному полю 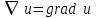 , получим скалярное поле , получим скалярное поле
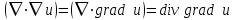
и векторное поле
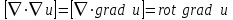
Если задано векторное поле 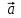 , то действие оператора Гамильтона на него порождает в нем скалярное поле , то действие оператора Гамильтона на него порождает в нем скалярное поле 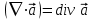 и векторное поле и векторное поле 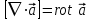 . Повторное применение оператора Гамильтона к векторному полю . Повторное применение оператора Гамильтона к векторному полю 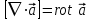 порождает скалярное поле порождает скалярное поле
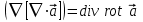
и два векторных поля:
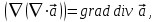 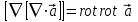
|
 Скачать 3.75 Mb.
Скачать 3.75 Mb.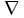 (читается «набла»; набла – древний музыкальный инструмент треугольной формы) и в декартовой системе координат имеет вид
(читается «набла»; набла – древний музыкальный инструмент треугольной формы) и в декартовой системе координат имеет вид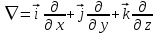 .
.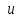 порождает векторное поле
порождает векторное поле 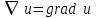 . Если повторно применить оператор
. Если повторно применить оператор 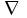 к векторному полю
к векторному полю 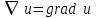 , получим скалярное поле
, получим скалярное поле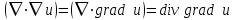
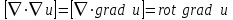
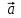 , то действие оператора Гамильтона на него порождает в нем скалярное поле
, то действие оператора Гамильтона на него порождает в нем скалярное поле 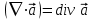 и векторное поле
и векторное поле 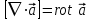 . Повторное применение оператора Гамильтона к векторному полю
. Повторное применение оператора Гамильтона к векторному полю 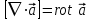 порождает скалярное поле
порождает скалярное поле 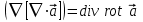
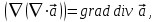
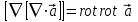

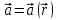 радиус-вектора точки или как вектор-функцию трех скалярных переменных
радиус-вектора точки или как вектор-функцию трех скалярных переменных 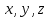 :
: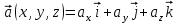 .
.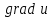 , которое определено в каждой точке пространства, если известно скалярное поле
, которое определено в каждой точке пространства, если известно скалярное поле 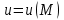 .
.
 Векторные линии веторного поля
Векторные линии веторного поля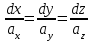 .
.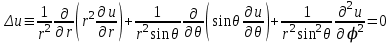 . (4.10)
. (4.10)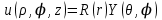 . (4.11)
. (4.11)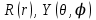 получим уравнения
получим уравнения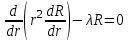 , (4.12)
, (4.12)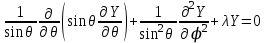 . (4.13)
. (4.13)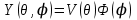 . (4.14)
. (4.14)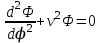 , (4.15)
, (4.15)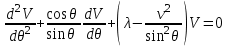 . (4.16)
. (4.16)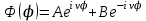 .
.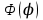 удовлетворяет условию цикличности
удовлетворяет условию цикличности 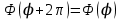 , то значение
, то значение 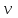 не может быть произвольным, а обязательно является целочисленным:
не может быть произвольным, а обязательно является целочисленным: 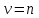 . Уравнение (4.16) называют обобщенным уравнением Лежандра.
. Уравнение (4.16) называют обобщенным уравнением Лежандра. 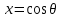 и обозначить
и обозначить 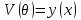 , то обобщенное уравнение Лежандра принимает обычный вид:
, то обобщенное уравнение Лежандра принимает обычный вид: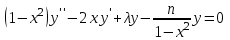
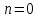 это уравнение имеет более простую форму уравнения Лежандра:
это уравнение имеет более простую форму уравнения Лежандра: 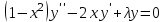 .
.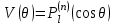 ,
, 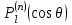 - присоединенные полиномы Лежандра, вычисляемые по формуле Родриго
- присоединенные полиномы Лежандра, вычисляемые по формуле Родриго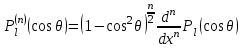 .
.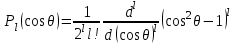 - полиномы Лежандра.
- полиномы Лежандра.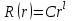 .
. 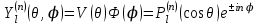 .
.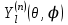 является частным ограниченным решением уравнения Лапласа:
является частным ограниченным решением уравнения Лапласа: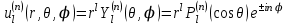 .
.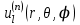 называют шаровыми. Общее решение уравнения Лапласа имеет вид:
называют шаровыми. Общее решение уравнения Лапласа имеет вид: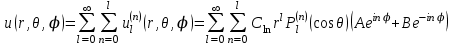 .
.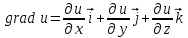
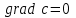 , где
, где 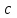 – постоянная;
– постоянная;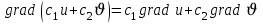 , где
, где 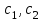 - постоянные;
- постоянные;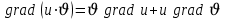 ;
;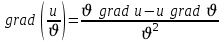 ;
;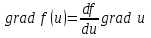 .
.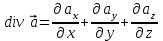 ;
; 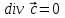 ,
, 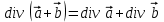 ;
;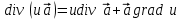 .
.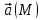 через бесконечно малую площадку
через бесконечно малую площадку 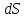 называется величина
называется величина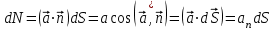 ,
,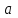 - значение векторного поля на площадке
- значение векторного поля на площадке 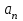 - проекция вектора
- проекция вектора 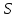
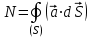 .
.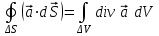 . (1.7)
. (1.7)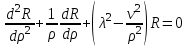
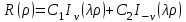 ,
,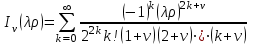 - бесселева функция первого рода порядка
- бесселева функция первого рода порядка 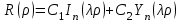 ,
, 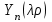 - функция Бесселя второго рода, которую еще называют функцией Неймана.
- функция Бесселя второго рода, которую еще называют функцией Неймана.