|
|
вавм. Билеты методы математический физики 2022 фипк-211. Дайте определение скалярного поля. Приведите примеры скалярного поля. Покажите как графически изображается скалярное поле. Приведите примеры.
24-Билет
№
|
|
1
|
Назовите характеристики векторного поля. Дайте инвариантное определение и физический смысл ротора векторного поля. Запишите формулы для вычисления ротора векторного поля в декартовых, цилиндрических и сферических координатах.
Основные характеристиками векторного поля являются дивергенция и ротор.
Ротор векторного поля — вектор, проекция которого на каждое направление равна пределу отношения циркуляции векторного поля по контуру L плоской площадки ΔS, перпендикулярной к этому направлению, к величине этой площадки, когда размеры площадки стремятся к нулю, а сама площадка стягивается в точку:
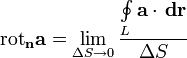
Физический смысл циркуляции в силовом поле состоит в том, что она равна работе по перемещению точки вдоль кривой в заданном направлении.
Ротор векторного поля A в точке M с криволинейными координатами определяется формулой
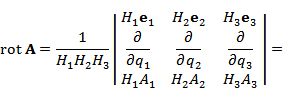 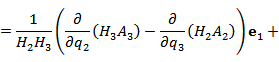
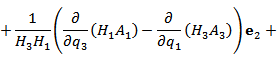 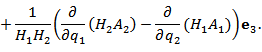
В цилиндрической системе координат
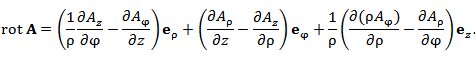
В сферических координатах
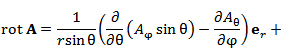 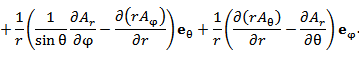
|
2
|
Дайте определение уравнения эллиптического типа. Приведите примеры уравнений эллиптического типа. Покажите как уравнение эллиптического типа приводится к каноническому виду.
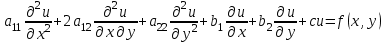 1 1
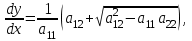 2 2
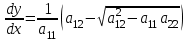 3 3
В данном уравнении (1) если 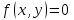 , то уравнение называется однородным, если же , то уравнение называется однородным, если же 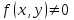 , то уравнение называется неоднородным. , то уравнение называется неоднородным.
В зависимости от значения коэффициентов, стоящих при старших производных, уравнения подразделяются на несколько типов. если 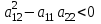 , то – уравнением эллиптического типа. , то – уравнением эллиптического типа.
Если уравнение (1) эллиптического типа, то общие интегралы уравнений (2) и (3) комплексно-сопряженные: 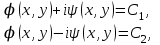
где 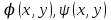 - вещественные функции, определяющие два семейства мнимых характеристик уравнения (1). Произведя замену переменных по формулам - вещественные функции, определяющие два семейства мнимых характеристик уравнения (1). Произведя замену переменных по формулам 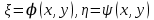 , приведем уравнение (1) к виду , приведем уравнение (1) к виду 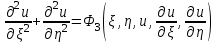 , ,
называемому каноническим видом уравнения эллиптического типа.
К уравнениям эллиптического типа относятся: уравнения Пуассона 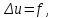 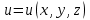 , уравнение Лапласа , уравнение Лапласа 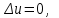 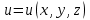 стационарное уравнение Шредингера стационарное уравнение Шредингера 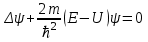 . .
| |
|
|
 Скачать 3.75 Mb.
Скачать 3.75 Mb.