Дифференциальных

• Название: Дифференциальных
• Дата: 08.06.2022
• Размер: 157.37 Kb.
• Имя файла: A.YU.-Krajnov-K.M.-Moiseeva-CHislennye-metody-resheniya-kraevyh-.docx
• Тип: Документы; #579564
• страница: 21 из 28

(2.47)

Задача заключается в том, чтобы найти такое значение s, при котором

решение задачи Коши (2.46) с граничными условиями (2.44), (2.47) удов- летворяет граничному условию (2.45). Иначе говоря, если решение зада-

чи Коши обозначить через y(x, s) и u(x, s), то требуется найти такое

значение s, что

y_l, s_  A  _s_  0.

(2.48)

В методе Ньютона итерационная формула для sзадается в виде

_s^n1 _{ s}ⁿ <sub>

 s</sub>ⁿ _

,

или
_s^n1 _{ s}ⁿ _

y_l,s^n _  A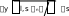

.

(2.49)

Чтобы найти производную yпо s,продифференцируем систему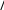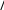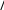

(2.46) с граничными условиями (2.44) и (2.47) по sи получим

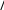dY dx  U,

и

dUdx _fy_Y

 _f

u_U

(2.50)

где

Y_0 _  0, U_0 _  1,

(2.51)

Y y

s,

U u

s.

(2.52)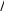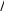

Решение системы уравнений (2.46), удовлетворяющее граничным ус- ловиям (2.44), (2.45) может быть получено следующими действиями.

1. 
   Выбирается значение s для недостающего начального значения производной (2.47). Это приближенное значение s обозначается через s⁽¹⁾.
   
2. 
   Интегрируется задача Коши (2.46) с граничными условиями за- данными в виде (2.44), (2.47) от x= 0 до x= l.
   
3. 
   Интегрируются уравнения (2.50) с начальными условиями (2.51)
   

от x = 0 до x = l.

4. 
   Значения y (l, s⁽¹⁾) и Y (l, s⁽¹⁾), подставляются в формулу (2.49),
   

что дает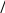


 
s⁽²⁾  s⁽¹⁾  ^y_l,s⁽¹⁾ _  A^ Y_l,s⁽¹⁾ _,

следующее приближение s⁽²⁾ для недостающего начального значения производной.

5. 
   Шаги 2 – 4 повторяются до тех пор, пока величина sне будет найдена с заданной точностью.