Дифференциальных

• Название: Дифференциальных
• Дата: 08.06.2022
• Размер: 157.37 Kb.
• Имя файла: A.YU.-Krajnov-K.M.-Moiseeva-CHislennye-metody-resheniya-kraevyh-.docx
• Тип: Документы; #579564
• страница: 18 из 28

(2.34)

Так как теперь ₀ (b) и ₁ (b) – известные величины, уравнения (2.33)

и (2.34) можно разрешить относительно y(b) и dy(b)/dxи получить

   
y_b_  ^ ₁₀  _{1 }b_^ / ^ _{0 }b_  ₀₀ ^ ,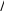


   
dy_b_ dx ^ ₀₀_{1 }b_  ₁₀ _{0 }b_^ / ^ ₀₀   _{0 }b_^ .

(2.35)

(2.36)

Теперь задачу Коши, определяемую уравнением (2.25) и начальными условиями (2.35) и (2.36), можно проинтегрировать назад от x= b. Дру-

гая возможность заключается в том, чтобы проинтегрировать (2.28), ис- пользуя (2.35) в качестве начального условия.

Пример: Рассмотрим решение следующей граничной задачи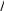

d²ydx²  y xcos x,

(2.37)

dy_0 _ dx 3y_0 _  2,

dy_

2 _ dx 5y_

2 _  2 ^.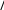

Известно точное решение этой задачи

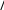y 0.73 cos x 0.441 sin x _1 4 _x² sin x xcos x_,

откуда

y_

2 _  0.175

^и dy_

2 _ dx 1.122.

Теперь найдем эти граничные значения, решая задачу методом про- гонки.

Сравнивая уравнения (2.37) и (2.25) получаем

p_x_  1, q_x_  xcos x,