Дифференциальных

• Название: Дифференциальных
• Дата: 08.06.2022
• Размер: 157.37 Kb.
• Имя файла: A.YU.-Krajnov-K.M.-Moiseeva-CHislennye-metody-resheniya-kraevyh-.docx
• Тип: Документы; #579564
• страница: 17 из 28

(2.29)

dx²

0 1 0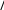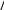

Заменив здесь dy/dxвыражением, стоящим в правой части уравнения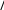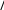

(2.28) получим

^d2^y _d

dx  ² _y d dx   .

(2.30)

dx²

0 0 1 0 1

Из сравнения с (2.25) получаем следующие уравнения: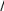

0 0
d _x_ dx  ²  p_x_,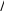

d_{1 }x_ dx  _{0 }x__{1 }x_  q_x_.

(2.31)

(2.32)

В качестве первого шага проинтегрируем на отрезке a< x< bурав-

нения (2.31) и (2.32) как задачу Коши, приняв в качестве начальных зна- чений

 _{0 }a_   ₀₀ , _{1 }a_  ₁₀ ,

получим значения ₀ (b) и ₁ (b). Подставив найденные значения в (2.28),

получим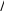

dy_b_ dx  _{0 }b_y_b_  _{1 }b_. ^(2.33)

С другой стороны, граничное условие (2.27) при x= bдает

dy_b_

dx ₀₀y_b_  ₁₀ .