Дифференциальных

• Название: Дифференциальных
• Дата: 08.06.2022
• Размер: 157.37 Kb.
• Имя файла: A.YU.-Krajnov-K.M.-Moiseeva-CHislennye-metody-resheniya-kraevyh-.docx
• Тип: Документы; #579564
• страница: 20 из 28

(2.41)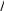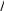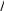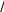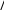

   

dy_ 2 _ dx 5y_ 2 _  2  1.122,

(2.42)

что согласуется с точным решением.

3. Методы решения краевых задач для нелинейных обыкно- венных дифференциальных уравнений второго порядка

Дифференциальные уравнения, содержащие неизвестные функции и их производные в степени выше первой или определенные каким-либо более сложным образом, называются нелинейными. Многие дифферен- циальные уравнения, описывающие физические явления, обычно линей- ны лишь в первом приближении. Детальное и более точное исследование физических явлений, как правило, приводит к нелинейным уравнениям. Решения нелинейных уравнений зачастую очень сложны, и их трудно представить простыми формулами. Значительная часть современной тео- рии решения нелинейных дифференциальных уравнений посвящена ка-

чественному анализу их поведения. Теория направлена на разработку методов, позволяющих, не решая уравнения, сказать нечто существенное о характере решений в целом: например, что все они ограничены, или имеют периодический характер, или определенным образом зависят от коэффициентов.

Приближенные решения нелинейных дифференциальных уравнений могут быть найдены численными методами. Именно при решении таких уравнений применяются итерационные методы.

1. Метод Ньютона

Рассмотрим краевую задачу, определяемую дифференциальным уравнением второго порядка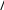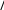

d²ydx²  f_x, y, dydx_

и граничными условиями

(2.43)

y_0_  0

y_l_  A

(2.44)

(2.45)

Запишем уравнение (2.43) в виде системы двух дифференциальных уравнений первого порядка


^_dydx u,

_dudx f_x,y,u_.

(2.46)

Обозначим недостающее начальное значение производной через s:

dy_0_ dx u_0_  s.