Дифференциальных
 Скачать 157.37 Kb. Скачать 157.37 Kb.
|
Метод квазилинеаризацииРассмотрим нелинейное дифференциальное уравнение второго по- рядка y fx, y, y С граничными условиями (2.53)y0 0, yL A, (2.54)где символами y'и y''обозначены соответственно dy/dxи d2y/d2x. Перепишем уравнение (2.53) в виде x, y, y, y y fx, y, y 0. (2.55)Чтобы получить рекуррентное соотношение, обозначим n- ю и (n+1) - ю итерации через ynи yn+1 и потребуем, чтобы для итераций вы- полнялось условие φ= 0. Это позволяет написать для n- й итерации yn fx, y, y 0. Для (n+1) - й итерации получаем xn1,yn1,yn1,yn1 xn,yn,yn ,yn (2.56)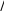 n1 n 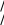 y yn1 yn y yn1 yn y yn1 yn y yn1 yn |
