Дифференциальных

• Название: Дифференциальных
• Дата: 08.06.2022
• Размер: 157.37 Kb.
• Имя файла: A.YU.-Krajnov-K.M.-Moiseeva-CHislennye-metody-resheniya-kraevyh-.docx
• Тип: Документы; #579564
• страница: 19 из 28

(2.38)

так, что уравнения (2.31) и (2.32) записываются в виде

0 0
d _x_ dx 1   ² _x_,

(2.39)

d_{1 }x_ dx xcos x  _{0 }x__{1 }x_.

Граничные условия таковы:

 _{0 }0 _  3,

_{1 }0 _  2.

Уравнения (2.39) можно проинтегрировать от x= 0 до x= .π/2

Так как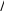

dy_x _ dx  _{0 }x _y_x_  _{1 }x _,

мы имеем

dy_

2 _ dx  _{0 }

2 _y_

2 _   _{1 }

2 _.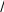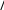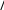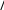

Учитывая, кроме того, граничное значение во второй точке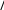

dy_ 2 _ dx 5y_ 2 _  2.

(2.40)

Можно разрешить систему уравнений (2.39), (2.40) относительно

y(π/2) и dy(π/2)/dx:

y_

2_  ^2  _{1 } 2_^ / ^5  _{0 } 2_^  0.176,