Дифференциальных

• Название: Дифференциальных
• Дата: 08.06.2022
• Размер: 157.37 Kb.
• Имя файла: A.YU.-Krajnov-K.M.-Moiseeva-CHislennye-metody-resheniya-kraevyh-.docx
• Тип: Документы; #579564
• страница: 23 из 28

(2.57)

или

 _

n n

y^ y^  y^  ...  0,

n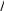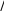

 _fy_{ }y_n1  y_n  _fy^_{ }y_n^ _1  y_n^ _  y_n^_1  y_n^  0.

(2.58)

n n


n
Подставляя в (2.58) выражение y^ из (2.56) получаем

y_n^_1  _f

y^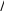



n

y_n^_1  _fy




n

n1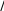


y 
 

(2.59)

 f_x,y_n,y_n  _f

y_

y_n _f

y_

y_n.

Граничные условия имеют вид

y_{n1 }0 _  0,

n n
y_{n1 }L_  A.

(2.60)

Уравнение (2.59) с граничными условиями (2.60) – это ли- нейная граничная задача, решение которой может быть по-

лучено одним из методов, применимых для решения линей- ных краевых задач (раздел 2.2).