Презентация логистика. Дипломная Работа (1). Дипломная работа тема работы Совершенствование логистических процессов на предприятии
 Скачать 1.41 Mb.
|
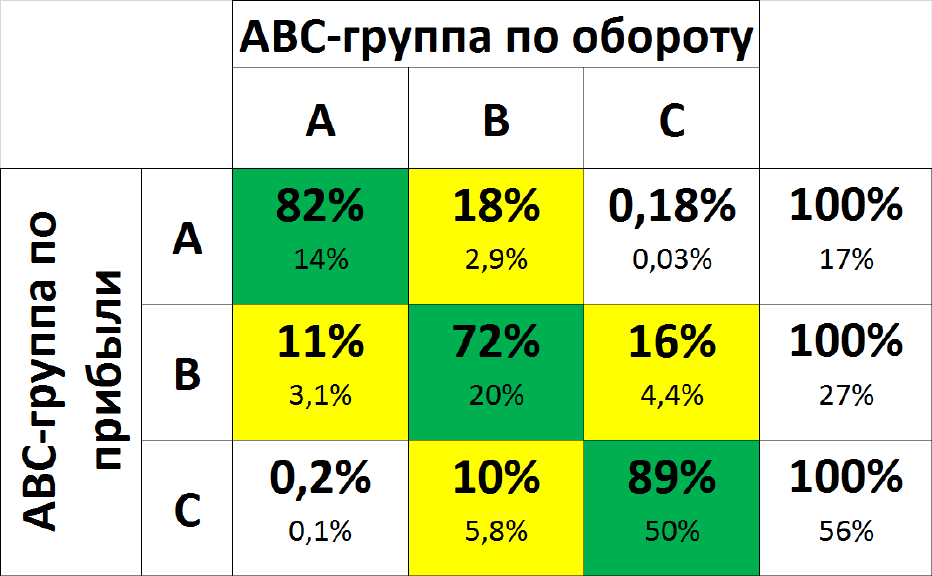 Рисунок 14 – ABC-анализ по прибыли/обороту [52] Влияние способа размещения продукции на складе на логистические затраты сложно переоценить – при любом изменении в объемах, ассортименте, многих технологических инновациях, при появлении нового покупателя либо расширении строительных работ собственного ДСК для оптимизации складской деятельности и ее затратности необходима перепланировка складских площадей. Наилучшим вариантом для оптимизации затрат динамичного производства считаем использование специализированных логистических программ, позволяющих быстро реагировать на произошедшие изменения. Для темы нашего исследования особый интерес представляет опыт зонирования складских площадей, представленный в работе «Оптимальное зонирование складских площадей» [22]. Его особенность – в использовании строгой реализации правила интенсивности оборота продукции (the intensity of the turnover of products – ITP) по критерию минимизации общих затрат на размещение и выемку продукции из мест хранения. В решении используются нестрогие допущения [22, с. 189]: Единственного пункта приемки и единственного пункта выдачи продукции; Единой технологии складской переработки продукции; Монотонно-возрастающего характера функции затрат на доставку грузовой единицы товара от (до) места хранения. Необходимо отметить, что данные допущения полностью применимы к системе складирования, принятой в складах готовой продукции большинства крупных предприятий по производству ЖБИ. Соответственно, мы считаем полностью применимым к теме нашего исследования исходного пункта постановки рассматриваемой задачи в рассматриваемой статье – «Это должны быть переменные типа «груз – адрес зоны хранения», которые являются как минимум двумерными. При этом если идентификация конкретных позиций грузов в первом приближении тривиальна, … то идентификация отдельных фрагментов площади склада допускает различные подходы» [22, с. 189]. Значительной сложностью для использования этого метода считаем необходимость квалифицированной математической подготовки специалиста для его «ручного» расчета даже в объеме исследовательской работы выпускника ВУЗа. Для решения оптимизационной задачи мы планируем разделение полезного пространства склада на определяемое целесообразное конечное число зон с возможностью их четкого позиционирования на складской площади и формированием транспортных траекторий к ячейке: от пункта приемки продукции (lj) и до пункта погрузки отправляемого груза (lj'), что может быть представлено матрицей булевых переменных ║Xij║, где i – индекс номенклатурной позиции груза, j – индекс (номер) ячейки, где может быть размещен груз. Если Xij = 1, то прибывшая партия i-го груза направляется в ячейку с номером j, если Xij = 0, то в какие-либо другие. Определение основных факторов зонирования – входящих/исходящих потоков производим следующим образом: для каждой (i-й) номенклатурной позиции они характеризуются средними размером партии (pi и pi' ) и интенсивностью (ŋi и ŋi').  M Тогда для каждого груза оптимальная ячейка в общем грузопотоке склада в формате переменной Xij будет представлена в соответствующей оптимизационной модели (8) [22, с. 189]: N L X f p ' f' p' min, i1 ij j1 i ij i i ij i Xij (8) где fijpi – функция затрат на обработку поступившей партии груза i- го типа, направляемой в j-ю ячейку, i ij f ' p' то же для партии груза i-го типа, которая из j-й ячейки доставляется к отгрузочной площадке склада. Ограничения единственности данных ячеек (9) [22, с. 190]:  Xiji1 1, для i = 1, N. (9) Проблему учета свободных ячеек можно решить «введением серии 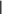 элементарных ограничений типа Xij = zij, где zij – нулевые элементы матрицы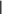 возможных размещенийZij , i = 1, N, j = 1, M. Остальные ее элементы равны максимальному количеству i-го груза, которое может вместить j-я ячейка» [22, с. 190] – мы предполагаем, что тарные емкости могут быть использованы для хранения нескольких типов грузов. Так сформированы оптимальные адреса, которые перенаправляют груз при занятости ячейки в ближайшую свободную, что соответствует монотонности функций fi по аргументу lj. Для учета существующих на любом складе ограничений по пропускной способности ячеек (количеству размещения/выемки в единицу времени) модель может быть дополнена ограничениями типа (10) [22, с. 190]: N X SВход X ' SВыход, ijij ijij N i1 ; i1 j 1, M , (10) где Вход S j и SВыход – предельные интенсивности работ по размещению и j выемке грузов для j-й ячейки, измеряемые партиями в единицу времени. В таком виде модель позволяет для каждой (i-й) грузовой позиции 1 2 ki получить вектор эффективной адресации вида Ri = { ji , ji ,… ji } – последовательность номеров ячеек, составленных в порядке убывания их предпочтительности для размещения i-го груза. Размер вектора Ri можно определить по реальному максимуму запаса Зi,max по формуле (11) [22, с. 191]: ki 2 Зi. max  Zij, j 1, M. (11)  Для получения векторов Ri можно использовать две возможности [22, с. 191]:а). В матрице Zij в каждой строке номера столбцов с ненулевыми значениями Zij (соответственно номера ячеек) сортируются в порядке убывания f f p i ' i i i соответствующих величин p' , т.е. учитывается стоимость переработки единицы груза по данной ячейке. Этот метод прост и нетрудоемок, но не учитывает, что те же самые ячейки используются для других грузов (грузы «конкурируют» между собой за наиболее привлекательные ячейки), а также возможность их занятости в конкретный момент. б). Данная процедура более трудоемка, но позволяет получить более  эффективный вектор адресации для каждого i-го груза. Адресi j 1 берется непосредственно из решения (11). Затем в матрице Zij удаляется i j 1 -му элементу присваивается нулевое значение и снова решается задача (41), ее решение дает адрес i j 2 . Далее для получения i j 3 принимается, что i |