Г. В. Плеханова (технический университет) к афедра общей и физической химии общая химия Сборник задач

• Название: Г. В. Плеханова (технический университет) к афедра общей и физической химии общая химия Сборник задач
• Анкор: Obschaya_khimia.doc
• Дата: 15.04.2018
• Размер: 2.09 Mb.
• Имя файла: Obschaya_khimia.doc
• Тип: Сборник задач; #18100
• страница: 15 из 27

5.3.2. Расчет рН в растворах слабых кислот и оснований

Диссоциация многих электролитов протекает не полностью. Отношение числа диссоциированных молей к общему числу молей электролита в растворе называют степенью диссоциации. Для его количественного описания используют константу равновесия, называемую константой диссоциации. Для одноосновной кислоты, диссоциирующей по уравнению:

НАn  Н+ + Аn, где Аn - кислотный остаток,
.	(62)

Т.к. [An^–] = [H⁺] и [An] = C то и

,

(63)

где С – концентрация слабой кислоты, моль/л K_d – константа диссоциации (приводится в справочниках).

Для растворов слабых оснований:

,

(64)

где С - концентрация слабого основания, моль/л.

По значению константы диссоциации можно рассчитать степень диссоциации слабого электролита:

.

(65)

Многоосновные кислоты диссоциируют ступенчато, например: Н₂S  НS^ + Н⁺ (1-ая ступень); НS^  S^ + Н⁺ (2-ая ступень).

При расчетах рН обычно учитывают только первую ступень диссоциации, пренебрегая второй и третьей ступенями. Таким образом, уравнения (62 и 64) справедливы и для многоосновных кислот при использовании первой константы диссоциации K_d1.

5.3.3. Примеры решения задач

Пример 1. Вычислить рН раствора серной кислоты концентрацией 0,3 % (d = 1,0 г/см³).

Решение. 1. Перейдем к моляльной концентрации серной кислоты. Для этого выделим мысленно 100 г раствора, тогда масса серной кислоты составит 0,3 г, а масса воды – 99,7 г. По уравнению (37) вычислим моляльную концентрацию: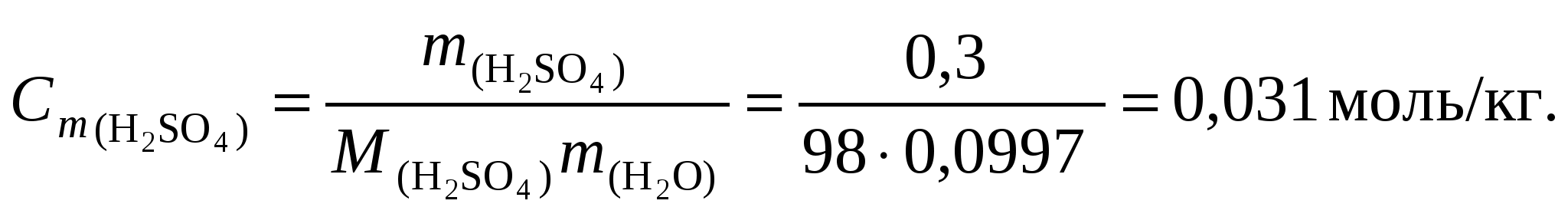



2. По уравнению диссоциации H₂SO₄  2H⁺ + SO₄^2 из 1 моль серной кислоты образуется 2 моль H⁺, следовательно,

3. По уравнению (50) вычислим значение рН:

рН = -lg[H⁺] = –lg0,062 = 1,21.

Пример 2. Вычислить рН раствора гидроксида бария концентрацией 0,0068 экв/л.

Решение. 1. По уравнению диссоциации Ba(OH)₂  Ba²⁺ + 2 OH^ из 1 моль гидроксида бария образуется 2 моль гидроксил-ионов:

3. По уравнению (50) найдем значение рОН:

рOН = -lg[OH^] = -lg0,0068 = 2,17

и вычислим рН:

рН = 14  рОН = 14 – 2,17 = 11,83.

Пример 3. Определить значение рН при разбавлении раствора одноосновной кислоты с рН = 5,5 в 100 раз.

Решение. По уравнению (56) найдем концентрацию ионов водорода в конечном растворе [H⁺]₂:

и вычислим его рН: рН₂ = -lg[H⁺]₂ = -lg1,1510^7 = 6,9.

Пример 4. Определить значение рН при смешении 10 л раствора с рН = 2 и 17 л раствора с рН = 4.

Решение. По уравнению (58) найдем концентрацию ионов водорода в конечном растворе [H⁺]₃



и вычислим рН₃: рН₃ = -lg[H⁺]₃ = -lg(4,610^3) = 2,33.

Пример 5. Смешали 250 мл раствора (V₁) с рН = 3 и 300 мл раствора (V₂) гидроксида калия концентрацией 0,001 моль/л. Определить рН полученной смеси.

Решение. 1. Найдем число молей OH^:



Согласно уравнению диссоциации: KOH  K⁺ + OH^,

2. Найдем число молей H⁺:



3. Очевидно, что в избытке находятся гидроксил-ионы. Их остаточную концентрацию в полученном растворе найдем по уравнению:

4. Вычислим рН₃ по уравнению:

рН₃ = 14 + lg[OH^]₃ = 14 + lg(9,110^5) = 9,96.

Пример 6. Найти рН раствора борной кислоты с мольной долей 0,0025 (d_р-р = 1,0 г/см³).

Решение. 1. выделим мысленно 1 кг раствора.

,

где индекс 1 относится к растворителю (т.е. к воде), а индекс 2 – к растворенному веществу, т. е. к H₃BO₃. M₁ = 18 г/моль, М₂ = 61,8 г/моль. , подставим в уравнение п. 1: и найдем n₂:



2. Так как плотность раствора равна 1 г/см³, то его объем соответствует 1 л и молярная концентрация численно равна количеству вещества борной кислоты, т. е. С_М(Н₃ВО₃) = 0,138 моль/л.

3. Диссоциация борной кислоты по первой ступени протекает по реакции: H₃BO₃  H⁺ + H₂BO₃^, для которой константа диссоциации K_d1 = 7,110^10. Второй и третьей ступенями диссоциации борной кислоты пренебрегаем.

4. рН раствора борной кислоты вычисляем в соответствии с уравнением (63):



рН = -lg[H⁺] = -lg(9,910^6) = 5.

Пример 7. Сколько граммов бутиламина содержится в 1 л его раствора, имеющего рН=11,5?

Решение. 1. Гидрат бутиламина диссоциирует как основание по уравнению: C₄H₉NH₂H₂O  C₄H₉NH₃⁺ + OH^. Константа диссоциации: K_d = 4,5710^4, pK_d = 3,340.

2. рОН = 14 - рН = 2,5.

3. Из формулы (64) находим молярную концентрацию бутиламина

lgC_М = pK_d – 2pOH = 3,34 - 22,5 = -1,66; C_М = 10^1,66 = 0,022 моль/л

и массу бутиламина, содержащуюся в 1 л раствора: С_г/л = C_МM,

где М – молярная масса бутиламина 73 г/моль.

Получаем С_г/л =0,02273 = 1,6 г/л.