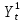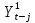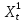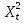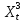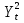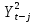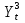финалочка моя. Характеристика инфраструктурных отраслей региона. 3
 Скачать 1.08 Mb. Скачать 1.08 Mb.
|
2.3 Расчет экспортного потенциала региона.1. Сформулировать цель анализа. Цель анализа: построить модель экспортной ориентации Архангельской области, представляющую собой систему одновременных эконометрических уравнений, которая показывает степень влияния одних факторов, характеризующих экспортный потенциал региона, на другие. 2. Выбор и обоснование экзогенных и эндогенных переменных. Для построения модели необходимо выбрать эндогенные и экзогенные переменные. Модель будет представлена в виде системы шести эконометрических уравнений. Каждое из уравнений будет представлять собой ADL-модель и содержать эндогенные и экзогенные переменные. Эндогенные факторы: Y1t – ВВП. Y2t – доля экспорта минеральных продуктов из Архангельской области. Y3t - доля экспорта лесоматериалов из Архангельской области. Экзогенные факторы: X1t – Глобальная конкурентноспособность. X2t – Население. X3t - Уровень доходов млн. рублей. X4t - Индекс производительности труда Архангельской области. X5t - ВРП Архангельской области млн. рублей. X6t - Объем экспорта минеральных продуктов млн. долларов США. Х7t- Объем экспорта лесной промышленности млн. долларов США. Собрать первичные статистические данные, данные изложить в виде таблиц. При необходимости провести обработку данных. Таблица 1
4) Отобразить взаимозависимость эндогенных и экзогенных показателей модели в виде таблицы (Таблица 2). Таблица 2 - Взаимозависимость эндогенных и экзогенных показателей модели
Эндогенные показатели находятся под влиянием предыстории процесса, экзогенных показателей и других эндогенных показателей (взаимовлияние эндогенных переменных). Составим структурную форму модели в общем виде на основе качественного анализа. 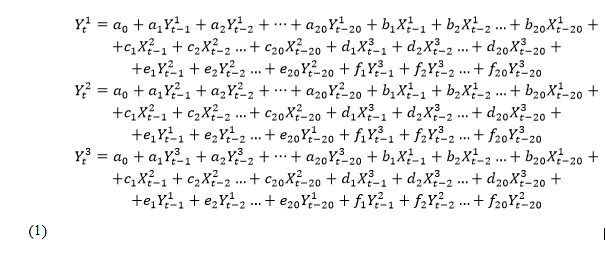 Структурной формой системы называется представление системы, в котором в уравнениях может присутствовать более одной эндогенной переменной (в стандартной записи это означает, что в правой части уравнений, то есть в качестве регрессоров, имеются эндогенные переменные). Структурная форма модели позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной. Использование МНК для оценивания структурных коэффициентов модели дает, как принято считать в теории, смещенные и несостоятельные оценки. Поэтому обычно для определения структурных коэффициентов модели структурная форма модели преобразуется в приведенную форму модели. Приведённой (прогнозной) формой системы называется представление системы, в котором в каждом уравнении имеется только одна эндогенная переменная, то есть эндогенные переменные выражены через экзогенные. 8
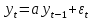 (2) (2)где 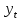 - временной ряд, а - временной ряд, а 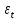 - ошибка. - ошибка.Если 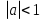 , то ряд стационарный. Если , то ряд стационарный. Если 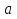 =1, то процесс имеет единичный корень, в этом случае ряд не стационарный, является интегрированным временным рядом первого порядка. =1, то процесс имеет единичный корень, в этом случае ряд не стационарный, является интегрированным временным рядом первого порядка. В том случае, если ряд нестационарный, привести его к стационарному виду путем вычисления разностей первого порядка.
Далее необходимо проверить коэффициенты парной корреляции на значимость с помощью t-критерия Стьюдента. Если tрасч > tтабл, то полученные коэффициенты значимы, т.е. выборка соответствует генеральной совокупности.
Проверка значимости коэффициентов автокорреляции по Q-статистике Льюнга-Бокса осуществляется по формуле: 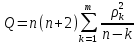 (3) (3)где n - число наблюдений, ρk - автокорреляция k-го порядка, и m - число проверяемых лагов. В случае если 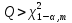 , коэффициенты считаются значимыми. , коэффициенты считаются значимыми. 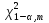 определяется по таблице. определяется по таблице.
Выполнение условия идентифицируемости модели проверяется для каждого уравнения системы и выполняется с целью определения вида МНК, который будет применяться для нахождения коэффициентов уравнений. Уравнение структурной формы называется идентифицируемым, если его коэффициенты можно выразить через коэффициенты приведённой формы. Если это можно сделать единственным способом, то говорят о точной идентифицируемости, если несколькими способами - о сверхидентифицируемости. В противном случае оно называется неидентифицируемым. Необходимые и достаточные условия идентификации применяются только к структурной форме системы одновременных уравнений. Необходимое условие идентифицируемости уравнения может быть записано в виде следующего счетного правила: D+1 = Н – уравнение идентифицируемо; D+1 < Н – уравнение неидентифицируемо; D+1 > Н – уравнение сверхидентифицируемо. где Н – число эндогенных переменных в i-ом уравнении системы; D – число экзогенных переменных, которые содержатся в системе, но не входят в данное уравнение. Достаточное условие идентификации определяется, если накладывать ограничения на коэффициенты матриц параметров структурной модели. Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного. Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение. D+1>H – уравнение сверхидентифицируемо. При сверхидентифицируемой модели, решить систему уравнений с использованием двух шагового МНК. Двух шаговый метод наименьших квадратов (ДМНК) — метод оценки параметров эконометрических моделей, в частности систем одновременных уравнений, состоящий из двух этапов (шагов), на каждом из которых применяется метод наименьших квадратов. Суть двух шагового метода наименьших квадратов заключается в следующем: Шаг 1. Обычным методом наименьших квадратов оценивается зависимость эндогенных переменных от всех экзогенных (фактически оценивается неограниченная приведённая форма). Шаг 2. Обычным методом наименьших квадратов оценивается структурная форма модели, где вместо эндогенных переменных используются их оценки, полученные на первом шаге. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. D+1=H – уравнение идентифицируемо. Уравнение идентифицируемо, если по отсутствующим в нем экзогенным и эндогенным переменным можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного. При решении идентифицируемой модели применяют косвенный МНК. Косвенный метод наименьших квадратов применяется только в том случае, если структурная форма системы одновременных уравнений будет точно идентифицированной. Алгоритм метода наименьших квадратов реализуется в три этапа: на базе структурной формы системы одновременных уравнений составляется её приведённая форма, все параметры кᴏᴛᴏᴩой выражены через структурные коэффициенты; приведённые коэффициенты каждого уравнения оцениваются обычным методом наименьших квадратов; на базе оценок приведённых коэффициентов системы одновременных уравнений определяются оценки структурных коэффициентов через приведённые уравнения. Для решения неидентифицируемых уравнений применяют двух шаговый МНК.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||