геометрия. геометрия 9 класс. Ход уроков I. Повторение ранее изученного материала
 Скачать 0.76 Mb. Скачать 0.76 Mb.
|
|
Вычитание векторов - ПОНЯТИЕ ВЕКТОРА. РАВЕНСТВО ВЕКТОРОВ (6 урок) Цели: ввести понятие разности двух векторов; научить строить разность двух данных векторов двумя способами; учить решению задач. Ход урока I. Анализ результатов самостоятельной работы. 1. Проанализировать характерные ошибки, допущенные в конт-рольной работе. 2. Решить на доске задачи, вызвавшие затруднения у учащихся. II. Объяснение нового материала. 1. Напомнить учащимся определение разности двух чисел: а – b = c, то a = c + b; например, 20 – 14 = 6, то 20 = 6 + 14. 2. Предложить учащимся самим «придумать» определение разности двух векторов. 3. Определение разности двух векторов (формулирует учитель): . 4. Рассмотреть задачу о построении разности двух векторов (рис. 256). 5. Введение понятия вектора, противоположного данному (рис. 257). Обозначение: вектор, противоположный вектору , обозначается так: – . Очевидно, . 6. Доказательство теоремы о разности векторов: для любых векторов справедливо равенство 7. Решение задачи о построении разности векторов другим способом (рис. 258). III. Решение задач и упражнений. 1. Выполнить практическое задание № 756. 2. Решить задачу № 762 (г) по готовому чертежу. 3. Решить задачу № 766 устно по рис. 259. 4. Решить задачу № 764 (а) на доске и в тетрадях. Решение а) Ответ: 5. Решить задачу № 765. Решение 1) 2) 3) Ответ: 6. Решить задачу № 772 на доске и в тетрадях. Доказательство Так как ABCD – параллелограмм, то Но IV. Проверочная самостоятельная работа. Вариант I Дан прямоугольный треугольник ABC с гипотенузой BC. Постройте вектор Вариант II Дан прямоугольный треугольник ABC с гипотенузой АВ. Постройте вектор Вариант III (для более подготовленных учащихся) Дана трапеция ABCD с основаниями АD и BC. Постройте вектор V. Итоги урока. Домашнее задание: повторить материал пунктов 76–82; вопросы 12, 13, с. 214; решить задачи №№ 757; 762 (д); 764 (б), 767. Основные требования к учащимся: В результате изучения параграфа учащиеся должны уметь объяснить, как определяется сумма двух и более векторов; знать законы сложения векторов, определение разности двух векторов; знать, какой вектор называется противоположным данному; уметь строить сумму двух и более данных векторов, пользуясь правилами треугольника, параллелограмма, многоугольника, строить разность двух данных векторов двумя способами, решать задачи типа №№ 759–771. Произведение вектора на число - ПОНЯТИЕ ВЕКТОРА. РАВЕНСТВО ВЕКТОРОВ (7 урок) Цели: ввести понятие умножения вектора на число; рассмотреть основные свойства умножения вектора на число. Ход урока I. Изучение нового материала (лекция). 1. Целесообразно в начале лекции привести пример, подводящий к определению произведения вектора на число, в частности такой: Автомобиль движется прямолинейно со скоростью . Его обгоняет второй автомобиль, двигающийся со скоростью, вдвое большей. Навстречу им движется третий автомобиль, у которого величина скорости такая же, как у второго автомобиля. Как выразить скорости второго и третьего автомобилей через скорость первого автомобиля и как изобразить с помощью векторов эти скорости? Ответ дает рисунок. Естественно считать, что скорость второго автомобиля равна 2 (произведению скорости первого автомобиля на число 2), а скорость третьего автомобиля равна –2 (произведению скорости на число –2). 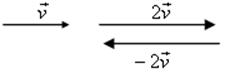 2. Определение произведения вектора на число, его обозначение: (рис. 260). 3. Записать в тетрадях: 1) произведение любого вектора на число нуль есть нулевой вектор; 2) для любого числа k и любого вектора векторы и коллинеарные. 4. Основные свойства умножения вектора на число: Для любых чисел k, l и любых векторов справедливы равенства: 1°. 2°. 3°. Примечание. Рассмотренные нами свойства действий над векторами позволяют в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, выполнять преобразования по тем же правилам, что и в числовых выражениях. Например. Ads by optAd360 II. Закрепление изученного материала. 1. Выполнить практические задания № 776 (б; г; д), 777. 2. Решить задачи № 779, 781 (а; в) на доске и в тетрадях. Решение Дано: а) в) 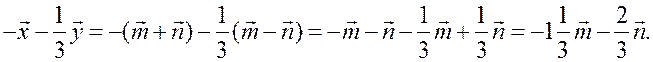 3. Решить задачу № 780 (б). III. Итоги урока. Домашнее задание: изучить материал пункта 83; ответить на вопросы 14–17, с. 214; решить задачи №№ 775, 776 (а, в, е), 781 (б), 780 (а). Решение задач. Произведение вектора на число - ПОНЯТИЕ ВЕКТОРА. РАВЕНСТВО ВЕКТОРОВ Цели: закрепить изученный материал в ходе решения задач; развивать логическое мышление учащихся. Ход урока I. Устная работа. По заранее заготовленным чертежам на доске устно решить задачи: 1. На рисунке 1 ABCD – параллелограмм, O – точка пересечения диагоналей. Выразите через векторы и векторы: а) б) 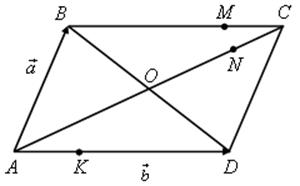 Рис. 1 2. На рисунке 2 ABCD – трапеция, О – точка пересечения диагоналей, ВС || AD, AD = 2BC. Выразите через векторы и векторы: а) б) 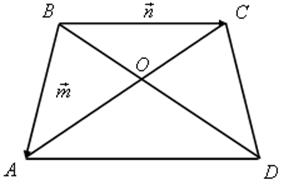 Рис. 2 II. Решение задач. 1. решить задачу № 782 на доске и в тетрадях. 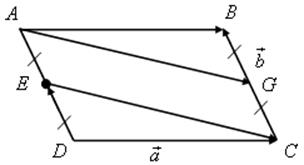 Ads by optAd360 Решение 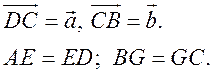 Из треугольника ECD (рис. 3) найдем по правилу вычитания векторов: 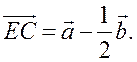 Из треугольника ABG по правилу сложения векторов имеем 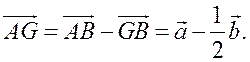 2. решить задачу № 802 на доске и в тетрадях. III. Проверочная самостоятельная работа. Вариант I 1. Начертите два неколлинеарных вектора и так, что = 3 см, = 2 см. Постройте 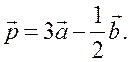 2. Четырехугольник KMNP – параллелограмм. Выразите через векторы Вариант II 1. Начертите два неколлинеарных вектора и так, что = 2 см, = 3 см. Постройте вектор 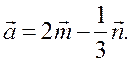 Ads by optAd360 2. В параллелограмме ABCD точка M – середина стороны CD; N – точка на стороне AD, такая, что AN : ND = 1 : 2. Выразите векторы и через векторы и . Вариант III (для более подготовленных учащихся) 1. В треугольнике ABC угол C = 90°, AC = 3 см, BC = 4 см. Постройте вектор 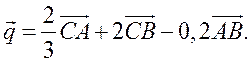 2. В трапеции ABCD AB || CD, AB = 3CD. Выразите через векторы и векторы и , где M – середина стороны BC, а N – точка на стороне AB, такая, что AN : NВ = 2 : 3. IV. Итоги урока. Домашнее задание: повторить материал пунктов 76–83; ответить на вопросы 1–17, с. 213–214 учебника; решить задачи №№ 783 и 804. Решение задач. Произведение вектора на число - ПОНЯТИЕ ВЕКТОРА. РАВЕНСТВО ВЕКТОРОВ (8 урок) Цели: закрепить изученный материал в ходе решения задач; развивать логическое мышление учащихся. Ход урока I. Устная работа. По заранее заготовленным чертежам на доске устно решить задачи: 1. На рисунке 1 ABCD – параллелограмм, O – точка пересечения диагоналей. Выразите через векторы и векторы: а) б)  Рис. 1 2. На рисунке 2 ABCD – трапеция, О – точка пересечения диагоналей, ВС || AD, AD = 2BC. Выразите через векторы и векторы: а) б)  Рис. 2 II. Решение задач. 1. решить задачу № 782 на доске и в тетрадях.  Ads by optAd360 Решение 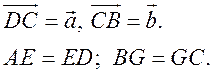 Из треугольника ECD (рис. 3) найдем по правилу вычитания векторов: 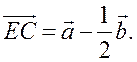 Из треугольника ABG по правилу сложения векторов имеем 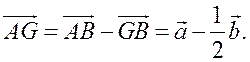 2. решить задачу № 802 на доске и в тетрадях. III. Проверочная самостоятельная работа. Вариант I 1. Начертите два неколлинеарных вектора и так, что = 3 см, = 2 см. Постройте 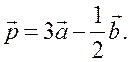 2. Четырехугольник KMNP – параллелограмм. Выразите через векторы Вариант II 1. Начертите два неколлинеарных вектора и так, что = 2 см, = 3 см. Постройте вектор 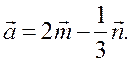 Ads by optAd360 2. В параллелограмме ABCD точка M – середина стороны CD; N – точка на стороне AD, такая, что AN : ND = 1 : 2. Выразите векторы и через векторы и . Вариант III (для более подготовленных учащихся) 1. В треугольнике ABC угол C = 90°, AC = 3 см, BC = 4 см. Постройте вектор 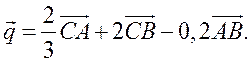 2. В трапеции ABCD AB || CD, AB = 3CD. Выразите через векторы и векторы и , где M – середина стороны BC, а N – точка на стороне AB, такая, что AN : NВ = 2 : 3. IV. Итоги урока. Домашнее задание: повторить материал пунктов 76–83; ответить на вопросы 1–17, с. 213–214 учебника; решить задачи №№ 783 и 804. Применение векторов к решению задач - ПОНЯТИЕ ВЕКТОРА. РАВЕНСТВО ВЕКТОРОВ (9 урок) Цели: на конкретных примерах показать применение векторов при решении геометрических задач; развивать логическое мышление учащихся, учить решать задачи. Ход урока I. Анализ результатов самостоятельной работы. 1. Указать ошибки учащихся при выполнении работ. 2. Решить задачи, вызвавшие затруднения у учащихся. II. Повторение изученного материала. 1. Ответить на вопросы на с. 213–214. 2. Вспомнить основные правила действий с векторами. 3. Решить задачи на доске и в тетрадях: 1) Упростите выражение 2) Найдите вектор из условия 4. Записать в тетрадях таблицу перевода с «геометрического» языка на «векторный»:
III. Работа по учебнику. 1. Векторы могут использоваться для решения геометрических задач. Рассмотрим вспомогательную задачу. 2. Разобрать решение задачи 1 на с. 208 учебника по рис. 264. IV. Решение задач. 1. Решить задачу 2. Точки M и N – середины сторон AB и CD четырехугольника ABCD. Докажите, что 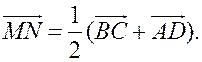 Ads by optAd360 Решение Пусть О – произвольная точка. Согласно задаче 1 из п. 84 имеем 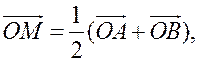 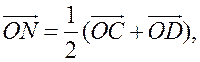 поэтому поэтому 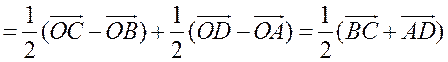 . .Примечание. Результат задачи 2 можно использовать при доказательстве теоремы о средней линии трапеции на следующем уроке. 2. Решить задачу 3. Точка С лежит на отрезке AB, причем АС : СВ = 2 : 3. Докажите, что для любой точки О справедливо равенство 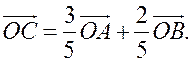 Решение По условию AC : CB = 2 : 3, поэтому 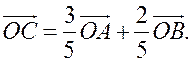 Примечание. Задача 3 является частным случаем более общей задачи 806. 3. Решить задачу № 784 на доске и в тетрадях. 4. Решить задачу № 786 на доске и в тетрадях. Решение Так как точка А1 – середина стороны ВС, то 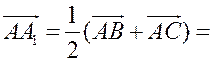 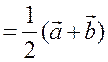 . .Далее 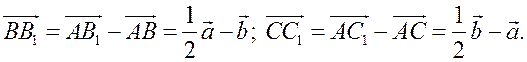 5. При наличии времени решить задачу 4. Ads by optAd360 Точки K, L, M, N – середины сторон AB, BC, CD, DE пятиугольника ABCDE, а точки P и Q – середины отрезков KM и LN. Докажите, что PQ || AE и PQ = 1/4 AE. 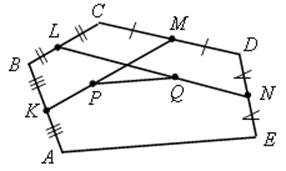 Решение Пусть О – произвольная точка. Согласно задаче 1 из п. 84 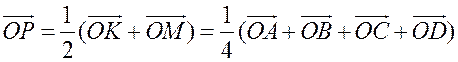 . Аналогично, . Аналогично, 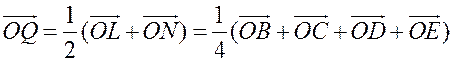 . .Из этих равенств следует, что 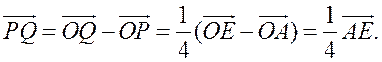 Отсюда следует, что PQ || AE и PQ = AE. Отсюда следует, что PQ || AE и PQ = AE.V. Итоги урока. Домашнее задание: повторить материал пунктов 76–84; разобрать решения задачи 2 из п. 84 и задачи № 788 и записать в тетрадь; решить задачу № 785. |
