геометрия. геометрия 9 класс. Ход уроков I. Повторение ранее изученного материала
 Скачать 0.76 Mb. Скачать 0.76 Mb.
|
|
Синус, косинус, тангенс. Основное тригонометрическое тождество - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА Урок 1. Синус, косинус, тангенс. Основное тригонометрическое тождество Цели: повторить определение синуса, косинуса и тангенса острого угла прямоугольного треугольника; ввести понятия синуса, косинуса и тангенса для углов от 0° до 180° и закрепить их знание в ходе решения задач. Ход урока I. Повторение ранее изученного материала. 1. Что называется синусом, косинусом, тангенсом острого угла прямоугольного треугольника? 2. Какое равенство называют основным тригонометрическим тождеством? 3. Чему равны значения синуса, косинуса и тангенса для углов 30°, 45° и 60°? II. Изучение нового материала. 1. Ввести понятие единичной полуокружности (рис. 290). ≤ 180°:2. Ввести понятие синуса и косинуса для углов 0° ≤ = х. = y; соs sin ≤ 180° синусом угла б называется ордината у точки М, а косинусом угла б – абсцисса х точки М, лежащей на единичной полуокружности.Таким образом, для любого угла б из промежутка 0° ≤ ≤ 1. ≤ 1; cos 0 ≤ sin 3. Нахождение значений синуса и косинуса для углов 0°, 90° и 180°. (4. Определение тангенса угла 90°): =tg 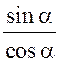 при 90°; tg 0° = 0; tg 180° = 0. при 90°; tg 0° = 0; tg 180° = 0.= 1, используя рисунок 290. + cos25. Вывести основное тригонометрическое тождество sin2 III. Закрепление изученного материала (решение задач). 1. Решить задачи № 1012 (для точек А, В, М1, М2). 2. Решить задачи № 1013 (б) на доске и в тетрадях. =Дано: cos . .Найти: sin Решени. Ads by optAd360 =; sin = 1 – cos2 = 1; sin2 + cos2 sin2 =sin 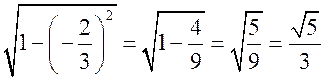 . .Ответ: . 3. Решить задачи № 1014 (а) и № 1015 (г). решение =г) sin и 90° < < расположен во II четверти, значит, cos 180°. Угол < , используя основное тригонометрическое тождество:0. Найдем cos = 1 – sin2cos2 =cos  ; ;.найдем tg =tg 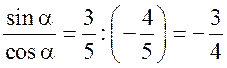 . .Ответ: . IV. Итоги урока. Домашнее задание: изучить материал пунктов 93 и 94; ответить на вопросы 1–4, с. 271; решить задачи № 1012 (для точек М2 и М3), №№ 1013 (б, в), 1014 (б, в), 1015 (б). Формулы приведения. Формулы для вычисления координат точки - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА Цели: вывести формулы для вычисления координат точки; развивать логическое мышление учащихся при решении задач. Ход урока I. Математический диктант (10–12 мин). Вариант I 1. Стороны прямоугольного треугольника равны 3 см, 4 см и 5 см. Найти синус, косинус и тангенс меньшего острого угла этого треугольника. 2. Катет прямоугольного треугольника равен 6 дм, а противолежащий угол равен 30°. Найдите гипотенузу этого треугольника. 3. Вычисляя синус острого угла, ученик получил число 1,05. Верны ли его вычисления? 4. Найти косинус острого угла, если его синус равен . 5. Найти тангенс острого угла, если его синус равен . 6. Синус острого угла прямоугольного треугольника равен . чему равен косинус второго острого угла этого треугольника? Вариант II 1. Стороны прямоугольного треугольника равны 10 дм, 8 дм и 6 дм. Найти синус, косинус и тангенс большего острого угла этого треугольника. 2. Катет прямоугольного треугольника равен 8 см, а противолежащий угол равен 45°. Найти гипотенузу этого треугольника. 3. Вычисляя косинус острого угла прямоугольного треугольника, ученик получил число 1,05. Верны ли его вычисления? 4. Найти синус острого угла, если его косинус равен . 5. Найти тангенс острого угла, если его косинус равен . 6. Косинус острого угла прямоугольного треугольника равен . чему равен синус второго острого угла этого треугольника? II. Изучение нового материала. 1. Обсудить с учащимися задачу № 1011. Ads by optAd360 2. Решить задачу: Используя единичную полуокружность, постройте угол: а) косинус которого равен ; ; 0; –1; б) синус которого равен ; ; 1. Для решения этой задачи полезно заготовить на доске несколько полуокружностей. 3. Предложить учащимся доказать, что синусы смежных углов равны, а косинусы смежных углов выражаются взаимно противоположными числами. 4. Записать формулы приведения: ≤ 180°; при 0° ≤ ) = – cos ; cos (180° – ) = sin sin (180° – ≤ 90°. при 0° ≤ ) = sin ; cos (90° – ) = cos sin (90° – 5. Объяснить учащимся содержание пункта 95 «Формулы для вычисления координат точки». III. Закрепление изученного материала (решение задач). 1. Решить задачу № 1016 на доске и в тетрадях. Решение sin 120° = sin (180° – 60°) = sin 60° = ; cos 120° = cos (180° – 60°) = –cos 60° = ; tg 120° = 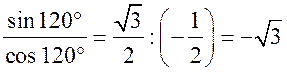 ; ;sin 135° = sin (180° – 45°) = sin 45° = ; Ads by optAd360 cos 135° = cos (180° – 45°) = –cos 45° = ; tg 135° = 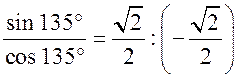 = –1. = –1.2. Решить задачу № 1018 (в). Решение = 150°; точка А (х; у) имеет координат.ОА = 5, = 5 ∙ cos 150° = 5 ∙ cos (180° – 30°) = –5 ∙ cos 30° =x = OA cos ; = 5 ∙ sin 150° = 5 ∙ sin (180° – 30°) = 5 ∙ sin 30° =y = OA sin = 2,5. A 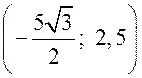 . .Ответ: x = ; y = 2,5. 3. Решить задачу № 1019 (в). Решение A ( ; 1); x = , y = 1. Решим сначала задачу в общем виде. Если известны координаты х и у точки А и х , разделив первое из них почленно на второе, получаем, х = ОА ∙ cos 0, то из равенств у = ОА ∙ sin 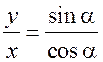 , то есть ., а из этого равенства можно с помощью таблиц или микрокалькулятора найти значение = tg , то есть ., а из этого равенства можно с помощью таблиц или микрокалькулятора найти значение = tg Ads by optAd360 , y = OA sin x = ОА cos ., 1 = ОА cos = ОА cos =тогда tg 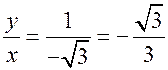 ; tg 30° = , а так как – < – тупой угол. расположен во II четверти, значит, 0, то угол ; tg 30° = , а так как – < – тупой угол. расположен во II четверти, значит, 0, то угол = 180° – 30° = 150°.Находим его: Ответ: 150°. IV. Итоги урока. Задание на дом: изучить материал пунктов 93–95; повторить материал пунктов 52, 66 и 67; решить задачи №№ 1017 (в), 1018 (б), 1019 (г). Решение задач - урок 2 - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА Цели: закрепить знания учащихся в ходе решения задач; развивать умения и навыки при решении задач. Ход урока I. Фронтальное повторение теоретического материала. Использовать настенную таблицу «Тригонометрические функции». ≤ 180°. из промежутка 0° ≤ 1. Объясните, что такое синус и косинус угла тангенс не определен и почему?? для какого значения 2. Что называется тангенсом угла 3. Записать основное тригонометрическое тождество. 4. Написать формулы приведения. 5. Написать формулы, выражающие координаты точки А с неотрицательной ординатой через длину отрезка ОА и угол между лучом ОА и положительной полуосью ОХ. II. Решение задач. , если:1. Решить задачу 1. Найти tg =а) cos ; = 1.б) sin 2. Решить задачу 2. Постройте β, если: а) cos β = ; б) sin β = . 3. Решить задачу № 1018 (г). решение ; х = 1 · cos 180° = –1; х = –1 = 180°; х = ОА cos ОА = 1; = 1 · sin 180° = 1 · 0 = 0; у = 0.y = ОА sin Ответ: х = –1; у = 0. III. Самостоятельная работа контролирующего характера. Вариант I Решить задачи №№ 1015 (а), 1017 (б), 1018 (а), 1019 (а). Ads by optAd360 Вариант II Решить задачи №№ 1015 (в), 1017 (а), 1018 (д), 1019 (б). IV. Итоги урока. Домашнее задание: повторить материал пунктов 93–95; повторить материал п. 52 «Площадь треугольника»; решить задачи №№ 468, 471, 469. Теорема о площади треугольника. Теорема синусов - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА Цели: доказать теорему о площади треугольника и теорему синусов; показать применение этих теорем при решении задач. Ход урока I. Проверка опорных знаний учащихся. Провести математический диктант (10 мин). Вариант I 1. Найдите площадь треугольника, если его основание равно 7 см, а высота равна 4 см. 2. Найдите синус угла, если его косинус равен . 3. Найдите синус угла, если синус смежного с ним угла равен 0,3. 4. Начертите треугольник АВС с тупым углом С. Проведите высоту треугольника из вершины В. 5. Луч ОС образует с положительной полуосью абсцисс угол 60°. Найдите координаты точки С, если ОС = 6 дм. 6. Определите, каким – остроугольным, прямоугольным или тупоугольным – является треугольник, два угла которого равны 43° и 48°. 7. Точка С единичной полуокружности имеет координаты 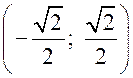 . Найдите угол, который образует луч ОС с положительной полуосью ОХ. . Найдите угол, который образует луч ОС с положительной полуосью ОХ.Вариант II 1. Найдите площадь треугольника, если его основание равно 10 дм, а высота равна 5 дм. 2. Найдите косинус угла, если его синус равен . 3. Найдите синус угла, если синус смежного с ним угла равен 0,7. 4. Начертите треугольник СDЕ с тупым углом Е. Проведите высоту треугольника из вершины С. 5. Луч ОВ образует с положительной полуосью абсцисс угол 30°. Найдите координаты точки В, если ОВ = 8 дм. 6. Определите, каким – остроугольным, прямоугольным или тупоугольным – является треугольник, два угла которого равны 35° и 56°. 7. Точка А единичной полуокружности имеет координаты 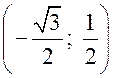 . найдите угол, который образует луч ОА с положительной полуосью ОХ. . найдите угол, который образует луч ОА с положительной полуосью ОХ.Ads by optAd360 II. Объяснение нового материала. 1. Доказательство теоремы о площади треугольника можно организовать в форме беседы по вопросам: 1) чему равна площадь любого треугольника? 2) какие формулы применяются для вычисления координат точки? 3) По рисунку 292 учебника провести доказательство теоремы о площади треугольника. 2. Устно решить задачу: найти площадь треугольника АВС, если АВ = 12 см, АС = 8 см, А = 30°. 3. Доказать теорему синусов, используя теорему о площади треугольника. III. Закрепление изученного материала (решение задач). 1. Решить задачу № 1020 (б) на доске и в тетрадях. Решение S = АВ · ВС sin B = ∙ 18 ∙ 3 sin 45° = 9 ∙ 3 ∙ = 27 (cм2). Ответ: 27 cм2. 2. Решить задачу № 1022. Решение S = 60 см2; S = АВ · AС sin A; 60 = AB · 15 sin 30°; 60 = АВ · ; АВ = 60 : = 16 (см). Ads by optAd360 Ответ: 16 см. 3. Решить задачу № 1026. Решение Используем теорему синусов: 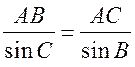 ; B = 180° – (60° + 75°) = 45°; ; B = 180° – (60° + 75°) = 45°;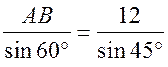 ; AB = ; AB = 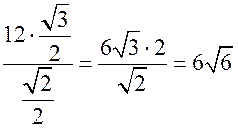 ≈ 15 (см). ≈ 15 (см).SΔABC = АC · AB sin A = · 12 · 15 sin 75° ≈ 87 (см2). Ответ: АВ ≈ 15 см; SАВС = 87 см2. IV. Итоги урока. Домашнее задание: изучить материал пунктов 96 и 97; повторить материал п. 89; решить задачи №№ 1020 (а, в), 1023. Теорема косинусов - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА Цели: доказать теорему косинусов и научить учащихся применять ее при решении задач. Ход урока I. Проверка домашнего задания. 1. Сформулировать и доказать теорему о площади треугольника (вычисление площади треугольника по двум сторонам и углу между ними). 2. Сформулировать и доказать теорему синусов. 3. Проверить решение задачи № 1023. II. Изучение нового материала. 1. Записать формулу расстояния между двумя точками: точки М1 (х1; у1), М2 (х2; у2), d = М1М2 = 2. Доказать теорему косинусов, используя рисунок 293 учебника. 3. Теорему косинусов называют иногда обобщенной теоремой Пифагора. Такое название объясняется тем, что в теореме косинусов содержится как частный случай теорема Пифагора. В самом деле, если в треугольнике АВС угол А прямой, то cos А = cos 90° = 0 и по формуле а2 = b2 + с2 – 2bс ∙ cos А получаем а2 = b2 + с2, то есть квадрат гипотенузы равен сумме квадратов катетов. 4. Обсудить с учащимися, какие три элемента треугольника нужно знать, чтобы вычислить четвертый элемент (сторону или угол), используя: 1) теорему синусов; 2) теорему косинусов. III. Решение задач. 1. Решить задачу 1. Найдите сторону АВ треугольника АВС, если ВС = 3 см, АС = 5 см, С = 60°. Решение АВ2 = ВС2 + АС2 – 2 ∙ ВС ∙ АС ∙ cos С = 32 + 52 – 2 ∙ 3 ∙ 5 cos 60° = 9 + 25 – 15 = 19; АВ = см. Ответ: см. 2. Решить задачу 2. Найдите сторону b треугольника АВС, если а = 4, с = и В = 135°. Решение По теореме косинусов находим b: b = 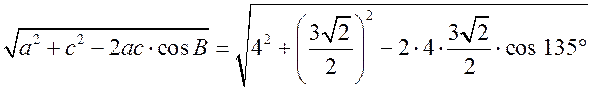 = =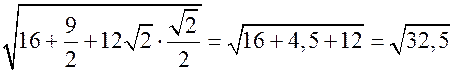 ≈ 5,7. ≈ 5,7.Ответ: ≈ 5,7. 3. Решить задачу 3. Найдите угол А треугольника АВС, если АВ = АС = 1 м, ВС = м. Решение Пользуясь теоремой косинусов, получаем: а2 = b2 + с2 – 2bс ∙ cos А; cos А = 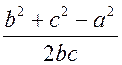 ; АС = b = 1 м; АВ = с = 1 м; ВС = а = м. cos А = ; АС = b = 1 м; АВ = с = 1 м; ВС = а = м. cos А = 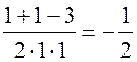 ; cos А = , тогда А = 120°. ; cos А = , тогда А = 120°.Ответ: 120°. Ads by optAd360 4. Решить задачу № 1031. Решение а) а = 5; b = 4; с = 4. Найдем cos А = 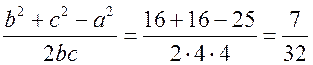 . Так как > 0, но меньше 1, то самый большой угол А в треугольнике будет острым. Следовательно, треугольник является остроугольным. . Так как > 0, но меньше 1, то самый большой угол А в треугольнике будет острым. Следовательно, треугольник является остроугольным.Ответ: остроугольный. б) а = 17; b = 8; с = 15. cos А = 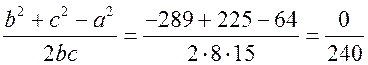 = 0; сos А = 0, значит, А = 90°. = 0; сos А = 0, значит, А = 90°.Ответ: прямоугольный. в) а = 9; b = 5; с = 6. cos А = 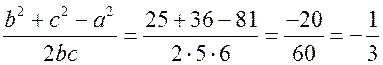 . .Так как –1 < < 0, то А – тупой. Ответ: тупоугольный треугольник. IV. итоги урока. Задание на дом: выучить материал пунктов 96–98; решить задачи №№ 1027, 1032. Решение треугольников - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА Цели: познакомить учащихся с методами решения треугольников; закрепить знание учащимися теорем синусов и косинусов, научить применять эти теоремы в ходе решения задач. Ход урока I. Проверка изученного материала. Учащиеся на отдельных листочках доказывают изученные теоремы и сдают учителю. Вариант I Сформулируйте и докажите теорему косинусов. Вариант II Сформулируйте и докажите теорему о площади треугольника. Вариант III Сформулируйте и докажите теорему синусов. II. Изучение нового материала. 1. Решением треугольника называется нахождение всех его шести элементов (то есть трех сторон и трех углов) по каким-нибудь трем данным элементам, определяющим треугольник. 2. При решении треугольников используют теоремы синусов и косинусов, причем при вычислении углов треугольника предпочтительнее использовать теорему косинусов, а не теорему синусов. Например, зная три стороны треугольника, для вычисления первого угла применяем теорему косинусов, а для вычисления второго угла можно использовать как ту, так и другую теоремы. Но поскольку синус угла равен синусу смежного с ним угла, то нахождение синуса угла еще не позволяет определить сам угол – он может быть острым или тупым. Если же вычислить косинус угла, то по его знаку и величине угол определяется однозначно. 3. Рассмотрим три задачи на решение треугольника: 1) решение треугольника по двум сторонам и углу между ними; 2) решение треугольника по стороне и прилежащим к ней углам; 3) решение треугольника по трем сторонам. При этом будем пользоваться следующими обозначениями для сторон треугольника АВС: АВ = с; ВС = а; СА = b. 4. В тетрадях учащиеся оформляют таблицу-памятку:
Ads by optAd360 III. Решение задач. 1. По рисунку 294 учащиеся самостоятельно разбирают решение примера на странице 259 учебника. 2. Решить задачу № 1025 (б, в, г, ж, и) на доске и в тетрадях, используя таблицы Брадиса и микрокалькуляторы. 3. Решить задачу № 1021 на доске и в тетрадях. 4. Совместно с учащимися разобрать и зафиксировать в тетрадях решение задачи № 1033 по рисунку 297. 5. Решить задачи № 1060 (в), 1061 (в) и 1062. IV. Итог урока. Задание на дом: изучить материалы пунктов 96–99; решить задачи №№ 1025 (а, д, е, з), 1060 (г), 1028. |

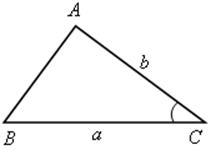
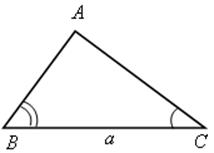
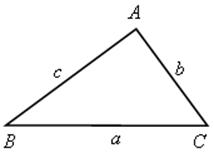
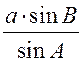 ;
;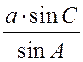
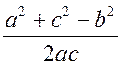 ;
;