геометрия. геометрия 9 класс. Ход уроков I. Повторение ранее изученного материала

• Название: Ход уроков I. Повторение ранее изученного материала
• Анкор: геометрия
• Дата: 25.01.2022
• Размер: 0.76 Mb.
• Имя файла: геометрия 9 класс.docx
• Тип: Решение; #341433
• страница: 9 из 9

Контрольная работа № 4 - ДВИЖЕНИЯ

Цели: проверить знания, умения и навыки учащихся в решении задач по теме «Движения».

Ход урока

I. Организация учащихся на выполнение работы.

II. Выполнение работы по вариантам.

Вариант I

1. Дана трапеция АВСD. Постройте фигуру, на которую отображается эта трапеция при симметрии относительно прямой, содержащей боковую сторону АВ.

2. Две окружности с центрами О1 и О2, радиусы которых равны, пересекаются в точках М и N. Через точку М проведена прямая, параллельная О1О2 и пересекающая окружность с центром О2 в точке D. используя параллельный перенос, докажите, что четырехугольник О1МDО2 является параллелограммом.

Вариант II

1. Дана трапеция АВСD. Постройте фигуру, на которую отображается эта трапеция при симметрии относительно точки, являющейся серединой боковой стороны СD.

2. Дан шестиугольник А1А2А3А4А5А6. Его стороны А1А2 и А4А5, А2А3 и А5А6, А3А4 и А6А1 попарно равны и параллельны. Используя центральную симметрию, докажите, что диагонали А1А4, А2А5, А3А6 данного шестиугольника пересекаются в одной точке.

Вариант III

1. Дана трапеция АВСD с основаниями АD и ВС. Постройте фигуру, на которую отображается эта трапеция при повороте вокруг точки А на угол, равный углу DАВ, по часовой стрелке.

2. На одной стороне угла ХОY отложены отрезки ОА и ОВ, а на другой стороне – отрезки ОМ и ОN так, что ОМ = ОА, ОN = ОВ. Используя осевую симметрию, докажите, что точка пересечения отрезков МВ и АN лежит на биссектрисе угла ХОY.

Вариант IV

1. Дана трапеция АВСD с основаниями АD и ВС. Постройте фигуру, на которую отображается эта трапеция при параллельном переносе на вектор .

2. На биссектрисе внешнего угла при вершине С треугольника АВС взята точка М. Используя осевую симметрию, докажите, чт.

АС + СВ < АМ + МВ.

Домашнее задание: повторить пункты 27–28 «Об аксиомах геометрии» и «Аксиома параллельных прямых».

Треугольник - РЕШЕНИЕ ЗАДАЧ

при повторении курса геометрии необходимо сконцентрировать внимание учащихся на узловых вопросах программы.

Основные факты планиметрии и применяемые в ней методы можно сгруппировать по следующим темам:

1. «Треугольник» (2 часа).

2. «Окружность» (2 часа).

3. «Четырехугольники, многоугольники» (2 часа).

4. «Векторы, метод координат, движения» (2 часа).

Рассмотрение этих вопросов может включать обобщение и систематизацию сведений об основных свойствах геометрических фигур, доказательство отдельных теорем, решение комплексных задач.

При повторении полезно обращать внимание учащихся на различные методы геометрических доказательств. В зависимости от подготовки класса повторение можно проводить по всем или отдельным вопросам рассматриваемой темы.

Для организации итогового повторения можно воспользоваться подбором задач по указанным выше темам

Треугольник

Основные вопросы программы: равенство и подобие треугольников, сумма углов треугольника, равнобедренный треугольник, прямоугольный треугольник, площадь треугольника.

Задачи

1. В треугольниках АВС и DЕK АВ = DЕ, АС = DK, ВР = ЕМ, где Р и М – середины сторон АС и DK.

1) Докажите, что треугольник АВС равен треугольнику DЕK.

АВС, если ЕМ = 3 см, DK = 42) Найдите Sсм, ЕМK = 135°.

2. В треугольниках АВС и А1В1С1 АС = А1С1, ВС = В1С1, ВD = В1D1, где ВD и В1D1 – высоты треугольников, причем точки D и D1 лежат на отрезках АС и А1С1.

1) Докажите, что треугольник АВС равен треугольнику А1В1С1.

2) Найдите радиус окружности, описанной около треугольника В1D1С1, если известно, что ВD = 6 см, DС = 8 см.

3) Найдите угол А1С1В1, если ВD = 6 см, DС = 8 см.

3. На рисунке дан прямоугольный треугольник АВС с гипотенузой АВ, DЕ  АВ.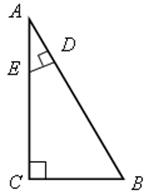



Ads by optAd360

1) Докажите, что треугольник АВС и треугольник DАЕ подобны.

2) Найдите катеты треугольника АВС, если АВ = 13 см, АЕ = 5,2 см, DЕ = 2 см.

3) Докажите, что около четырехугольника ВDЕС можно описать окружность.

4. В прямоугольном треугольнике АВС проведена высота СD к гипотенузе АВ, СD = а, АD = b.

найдите: 1) ВС; 2) радиус окружности, вписанной в треугольник АВС; 3) отношение площадей треугольников АDС и АСВ.

5. В треугольнике АВС АВ = 14 см, АС = 15 см, ВС = 13 см.

найдите: 1) длину меньшей высоты треугольника; 2) площадь треугольника АDС, если АD – биссектриса треугольника АВС; 3) медиану АЕ треугольника АВС.

6. С помощью циркуля и линейки постройте треугольник АВС по сторонам АВ и АС и высоте, проведенной к АС.

7. Площадь треугольника АВС равна Q. Найдите площадь треугольника АОВ1, где О – точка пересечения медиан треугольника АВС, а В1 – середина стороны АС.

8. С помощью циркуля и линейки постройте равнобедренный треугольник АВС по основанию АС и углу В и биссектрису ВD внешнего угла этого треугольника при вершине В.

Окружность - РЕШЕНИЕ ЗАДАЧ

Основные вопросы программы: окружность и круг, касательная к окружности и ее свойства; окружность, описанная около треугольника; окружность, вписанная в треугольник.

Задачи

1. Хорда АВ окружности радиуса 4 см видна из центра под углом 90°.

Найдите: 1) хорду АВ и расстояние от центра окружности до этой хорды; 2) углы треугольника АВС, где С – точка, расположенная на большой дуге АВ окружности так, что  АС :  СВ = 5 : 4; 3) хорду ВС.

2. Две взаимно перпендикулярные хорды АВ и СD окружности пересекаются в точке K, причем АK = 6 см, ВK = 32 см, KD = 24 см.

Найдите: 1) хорды ВD и СD; 2) расстояние от точки А до прямой ВD; 3) радиус данной окружности.

3. Треугольник АВС с углом В, равным 135°, вписан в окружность с центром О и радиусом R = 10см.

АВС, если известно, что угол АСВ равен 30°.Найдите: 1) сторону АВ; 2) сторону АВ и S

4. Точки М, D и K лежат на окружности, угол DМK равен 45°, хорда DK = 12 см.

Найдите: 1) радиус данной окружности; 2) угол МКD, если известно, что DМ = 6см.

5. Радиус окружности, вписанной в равнобедренный треугольник АВС с основанием АС, равен 3 см, KВ = 4 см, где K – точка касания окружности с боковой стороной.

Найдите: 1) сторону АС; 2) угол ВАС; 3) радиус окружности, описанной около треугольника АВС.

6. В равнобедренный треугольник АВС с основанием АС вписана окружность, касающаяся сторон АВ и ВС в точках М и Н.

1) Докажите, что треугольник МВН   треугольнику АВС.

2) Найдите угол ВАС и радиус окружности, если АВ = 2 м, МН = 1 м.

Четырехугольники. Многоугольники - РЕШЕНИЕ ЗАДАЧ

Основные вопросы программы: параллелограмм и его свойства; признаки параллелограмма; прямоугольник, ромб, квадрат и их свойства; трапеция, многоугольник, правильные многоугольники.

Задачи

1. На рисунке 1 АЕFС – прямоугольник; АС = 10 см, АЕ = 3 см, ВМ = АМ.

1) Докажите, что МN – средняя линия треугольника АВС.

АВС.2) Найдите SАМNС. 3) Найдите S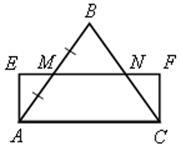



Рис. 1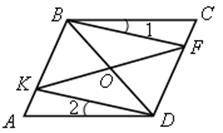


Рис. 2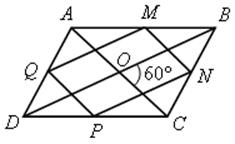


Рис. 3

.

2. В параллелограмме АВСD биссектриса угла А пересекает сторону ВС в точке Е; АВ = а; АD = b. Найдите: 1) отрезки ВЕ и ЕС; 2) отрезки ВK и KD и SАВЕ, если K – точка пересечения АЕ и ВD, а угол А равен 60°.

3. На рисунке 2 АВСD – параллелограмм, угол 1 равен углу 2.

1) Докажите, что четырехугольник ВFDK – параллелограмм, и найдите его площадь и периметр, если KF = 10 см, ВD = 6 см, KОD = 150°. 2) Каким условиям должны удовлетворять отрезки KF и ВD, чтобы параллелограмм ВFDK был прямоугольником (ромбом, квадратом)?

4. Меньшая диагональ параллелограмма перпендикулярна к его стороне, а высота, проведенная из вершины тупого угла, делит большую сторону на отрезки, равные 9 см и 16 см.

найдите: 1) стороны и высоту параллелограмма, проведенную из вершины тупого угла; 2) диагонали параллелограмма; 3) площадь параллелограмма.

Ads by optAd360

5. В параллелограмме АВСD проведена биссектриса АK угла А, точка K делит сторону ВС на отрезки ВK = 4 см и KС = 2см. Расстояние между параллельными прямыми АD и ВС равно 2см.

Найдите: 1) углы параллелограмма; 2) площадь треугольника АВС; 3) радиус окружности, описанной около треугольника DКС.

6. На рисунке 3 точки М, N, Р и Q – середины сторон четырехугольника АВСD, АС = 10 см, ВD = 18 см.

1) Докажите, что MNPQ – параллелограмм, и найдите его периметр. 2) Найдите площади четырехугольников АВСD и MNPQ, если угол ВОС равен 60°.

7. В равнобедренную трапецию, основания которой равны 2 см и 8 см, вписана окружность.

Найдите: 1) боковую сторону трапеции; 2) радиус вписанной окружности; 3) площадь трапеции.

8. В равнобедренной трапеции с основаниями АD и ВС угол D равен 60°, ВС = 12 см, а угол ВСА равен 30°.

1) Докажите, что треугольник АВС равнобедренный. 2) Найдите радиус окружности, описанной около треугольника АСD. 3) Найдите площадь трапеции АВСD.

9. В ромб, сторона которого равна диагонали и равна а, вписана окружность, а в эту окружность вписан правильный треугольник.

Найдите: 1) радиус окружности; 2) сторону треугольника; 3) площади ромба, круга и правильного треугольника.

10. Каждый угол правильного n-угольника А1А2… Аn равен 150°.

1) Найдите число сторон этого многоугольника. 2) Найдите А2А3А10. 3) Докажите, что треугольник А1А3В подобен треугольнику А6А10В, где В – точка пересечения диагоналей А1А6 и А3А10 этого многоугольника.

11. Внешний угол правильного n-угольника А1А2… Аn в три раза меньше угла этого многоугольника.

Ads by optAd360

1) Найдите число сторон этого многоугольника. 2) Найдите А3А1А6. 3) Докажите, что четырехугольник А1А3А4А8 – равнобедренная трапеция.

Векторы. Метод координат. Движения - РЕШЕНИЕ ЗАДАЧ

Основные вопросы программы: вектор, длина вектора, сложение векторов и его свойства, умножение вектора на число и его свойства, коллинеарные векторы, прямоугольные координаты точек на плоскости, формула расстояния между двумя точками плоскости с заданными координатами, координаты середины отрезка, уравнения окружности и прямой, применение векторов и метода координат к доказательству теорем и решению задач. Движения.

Задачи

1. Четырехугольник АВСD задан координатами своих вершин: А (–3; –2), В (–1; 2), С (2; 2), D (4; –2).

1) Найдите координаты середин сторон этого четырехугольника.

2) Докажите, что середины сторон четырехугольника АВСD являются вершинами ромба, и найдите площадь этого ромба.

2. Дан четырехугольник АВСD.

1) Определите вид четырехугольника АВСD, если 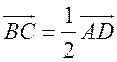 , и выразите вектор  через векторы   и  .

2) Выразите векторы   через векторы  и , если М, N, Р и Q – середины сторон АВ, ВС, СD и АD.

3) Определите вид четырехугольника МNPQ.

3. Дан правильный шестиугольник АВСDЕF со стороной а. Найдите скалярное произведение векторов: 1)  ; 2)  ; 3)  ; 4)  .

4. Найдите косинусы углов треугольника АВС, если А (1; 3), В (8; 2), С (5; –1).

5. В параллелограмме АВСD диагональ ВD равна стороне ВС, точка М – середина стороны ВС, отрезок DМ перпендикулярен к диагонали АС. Найдите углы параллелограмма.

6. Две окружности радиуса r с центрами О1 и О2 касаются друг друга в точке М. На первой окружности отмечена точка А, а на второй – точка В так, что хорды АМ и ВМ взаимно перпендикулярны. Докажите, что: 1) при параллельном переносе на вектор   отрезок АС отображается на отрезок ВМ; 2) АВ = 2r.

7. На сторонах правильного треугольника построены квадраты. Докажите, что центры этих квадратов являются вершинами правильного треугольника.