геометрия. геометрия 9 класс. Ход уроков I. Повторение ранее изученного материала
 Скачать 0.76 Mb. Скачать 0.76 Mb.
|
|
Площадь круга - ДЛИНА ОКРУЖНОСТИ. ПЛОЩАДЬ КРУГА Цели: вывести формулу площади круга и научить учащихся применять ее при решении задач. Ход урока I. Изучение нового материала (лекция). Провести в форме лекции доказательство площади круга. 1. Дать определение понятия «круг». 2. Вывести формулу площади круга (рис. 314). 3. Записать в тетрадях: для вычисления площади S круга радиуса R применяется формула . 4. В течение веков усилия многих математиков были направлены на решение задачи, получившей название задача о квадратуре круга: построить при помощи циркуля и линейки квадрат, площадь которого равна площади данного круга. Только в конце XIX века было доказано, что такое построение невозможно. II. Закрепление изученного материала (решение задач). 1. Решить задачу. На здании МГУ установлены часы с круговым циферблатом, имеющим диаметр примерно 8,8 м. Найдите площадь циферблата этих часов и сравните с площадью вашей классной комнаты. Ответ: 60,8 м2. 2. Решить задачу № 1118 (самостоятельно). 3. Решить задачу № 1119 на доске и в тетрадях. Решение С = 41 м; C = 2πR; D = 2R (диаметр D); 2R = D = ; D = ≈ 13,06 (м) ≈ 13,1 м. Sкруга = πR2; так как R = , то Sкруга = π ∙ 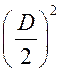 = π ∙ . = π ∙ .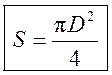 S = 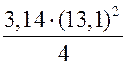 ≈ 133,84 (м2). ≈ 133,84 (м2).Ответ: ≈ 13,06 м; 133,84 м2. 4. Решить задачу № 1125 на доске и в тетрадях. На сторонах произвольного прямоугольного треугольника АВС, как на диаметрах, построены полукруги. Докажите, что сумма площадей полукругов, построенных на катетах, равна площади полукруга, построенного на гипотенузе. Ads by optAd360 Решени. 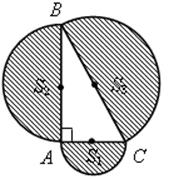 Пусть АС = 2а, АВ = 2b, ВС = 2с, тогда радиусы соответствующих кругов равны а, b, с. 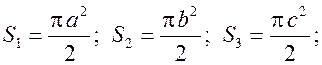 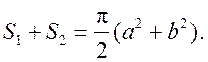 По теореме Пифагора а2 + b2 = с2, поэтому 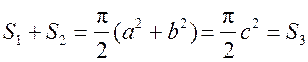 . .5. Решить задачу № 1116 (а) на доске и в тетрадях. Решение Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, а радиус описанной окружности равен половине гипотенузы. По теореме Пифагора находим: с2 = а2 + b2; тогда R = 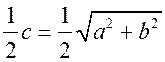 . .Значит, Sкруга = πR2 = 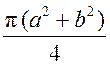 . .Ответ: 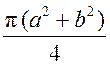 . .Ads by optAd360 III. Итоги урока. Домашнее задание: повторить материал пунктов 105–110; изучить материал пункта 111; решить задачи №№ 1114, 1115, 1117 (а). Площадь кругового сектора - ДЛИНА ОКРУЖНОСТИ. ПЛОЩАДЬ КРУГА Цели: ввести понятие кругового сектора, вывести формулу для вычисления площади кругового сектора; научить применять знания при решении задач. Ход урока I. Проверка изученного материала. 1. Формула длины окружности. Выражение радиуса окружности через длину окружности. 2. Формулы площади круга, радиуса круга через площадь круга, формула площади круга, выраженная через диаметр круга. 3. Формула длины дуги окружности. 4. Устно решить задачу № 1115. II. Объяснение нового материала. 1. Ввести понятие кругового сектора и понятие дуги сектора (рис. 315). .2. Вывести формулу для вычисления площади S кругового сектора радиуса R, ограниченного дугой с градусной мерой Так как площадь всего круга равна πR2, то площадь кругового сектора, ограниченного дугой в 1°, равна 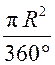 . .Поэтому площадь S выражается формулой S = 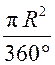 ∙ ∙ 3. Ввести понятие кругового сегмента и познакомить учащихся с нахождением площади кругового сегмента, используя таблицу «Круговой сегмент». III. закрепление изученного материала (решение задач). 1. Решить задачу. АВСD – квадрат со стороной 1 дм. Найдите площадь «чечевицы», заштрихованной на рисунке. 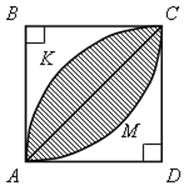 Решение Так как сторона квадрата равна 1 дм, то площадь квадрата АВСD равна 1 дм2. Площадь сектора DАKС равна 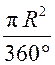 =∙ ∙ 90° = (дм2). =∙ ∙ 90° = (дм2).Ads by optAd360 Площадь треугольника АСD равна дм2. Площадь сегмента АKС равна 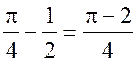 (дм2). (дм2).Площадь «чечевицы»: 2 ∙ 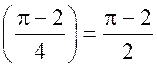 ≈ 0,7 (дм2). ≈ 0,7 (дм2).Ответ: ≈ 0,7 дм2. 2. Решить задачу № 1126 (самостоятельно). Решение R = 10 см; Sкруга = πR2 = 100π (см2). = 60°; Sсектора =l = 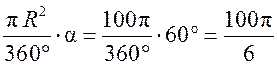 (см2). (см2).S = Sкруга – Sсектора = 100π – 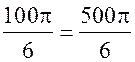 ≈ 262 (cм2). ≈ 262 (cм2).Ответ: ≈ 262 см2. 3. Решить задачу № 1127. Решение = 72°, Sсектора = S. Найти: R. S = 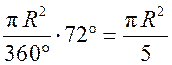 ; 5S = πR2; R2 = ; R = . ; 5S = πR2; R2 = ; R = .Ответ: . Ads by optAd360 4. Вывести формулу площади кольца, ограниченного двумя окружностями с общим центром и радиусами R1 и R2, где R1 < R2. Решени. 5. Решить задачу № 1120. Решение R1 = 1,5 cм, R2 = 2,5 см. Sкольца = π (2,52 – 1,52) = π (2,5 – 1,5) (2,5 + 1,5) = π ∙ 1 ∙ 4 = 4π (см2). Ответ: 4π см2. 6. Решить задачу № 1122 на доске и в тетрадях. Решение R1 = 3 м, R2 = 3 + 1 = 4 (м). Sдорожки = π На 1 м2 дорожки требуется 0,8 дм3 песка; тогда 0,8 ∙ 7π = 5,6π (дм3) ≈ 17,6 дм3. Ответ: ≈ 17,6 дм3. IV. Итоги урока. Домашнее задание: выучить материал пунктов 110–112; повторить материал пунктов 105–109; ответить на вопросы 1–12 на с. 290; решить задачи № 1121, 1128, 1124. Решение задач - урок 5 - ДЛИНА ОКРУЖНОСТИ. ПЛОЩАДЬ КРУГА Цели: закрепить знания учащихся по изученной теме «Длина окружности и площадь круга»; научить учащихся применять изученные формулы при решении задач; развивать логическое мышление учащихся. Ход урока I. Актуализация опорных знаний учащихся. 1. Повторить определения окружности, круга, кругового сектора и кругового сегмента. 2. Записать на доске и в тетрадях формулы для вычисления длины окружности, длины дуги окружности; для вычисления площади круга, площади кольца, площади кругового сектора. II. Решение задач. 1. Решить задачу № 1112. Решение l = = 38°. Найдем: R: R =; l = 24 см; ∙ 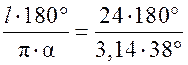 ≈ 36,3 (см). ≈ 36,3 (см).ответ: ≈ 36,3 см. 2. Решить задачу № 1113 (самостоятельно). 3. Решить задачу № 1123 на доске и в тетрадях. Решение 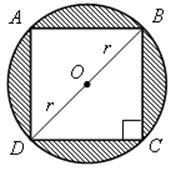 АВСD – квадрат; DО = ОВ = r; Sкруга = πr2; Sквадрата = а2, ВD = 2r; из ДВСD по теореме Пифагора найдем сторону квадрата АВСD: а2 + а2 = (2r)2; 2а2 = 4r2; а2 = 2r2; тогда Sквадрата = 2r2. Найдем площадь оставшейся части круга: S = Sкруга – Sквадрата = πr2 – 2r2 = r2 (π – 2). Ответ: r2 (π – 2). 4. Решить задачу № 1116 (б). 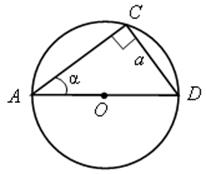 Ads by optAd360 Решени. АСD – прямоугольный; , СD = а. АD = 2R (диаметр),А = АСD = 90° (вписанный угол, опирающийся на диаметр, прямой). Найдем АD. =Sin ; AD = , тогда радиус R описанной около прямоугольного треугольника окружности равен R =AD = 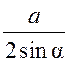 . Площадь круга равна S = πR2 = . Площадь круга равна S = πR2 =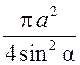 . .Ответ: 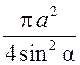 . .5. Решить задачи: 1) Площадь кругового кольца, заключенного между двумя окружностями с одним и тем же центром, равна 12 дм2. Найдите радиусы окружностей, если один их них в два раза больше другого. Ответ: дм; дм. 2) Площадь кругового кольца, заключенного между двумя окружностями с одним и тем же центром, равна 8 см2. Найдите площади этих кругов, ограниченных этими окружностями, если радиус одной из них в три раза больше, чем радиус другой. Ответ: 1 см2 и 9 см2. 6. Решить задачу № 1108 (самостоятельно). III. Самостоятельная работа (10–15 мин). Вариант I Ads by optAd360 Решить задачи №№ 1102 (в), 1115 (б), 1109 (в), 1104 (б). Вариант II Решить задачи №№ 1102 (г), 1115 (а), 1109 (г), 1116 (а). IV. Итоги урока. Домашнее задание: повторить материал пунктов 105–112; решить задачи №№ 1107, 1132, 1137. Решение задач по материалу главы XII - ДЛИНА ОКРУЖНОСТИ. ПЛОЩАДЬ КРУГА (2 урока) Цели: закрепить знания и умения учащихся по изученному материалу главы; подготовить учащихся к контрольной работе. Ход уроков I. Математический диктант (15 мин). Вариант I 1. Площадь круга равна S. Найдите длину ограничивающей его окружности. 2. Найдите длину дуги окружности радиуса 9 м, если градусная мера дуги равна 120°. 3. Длина дуги окружности равна 3π, а ее радиус равен 8. Найдите градусную меру этой дуги. 4. Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 13 и 12 см. 5. Найдите площадь кругового сектора радиуса 4 см, если его центральный угол равен 45°. 6. Площадь кругового сектора равна 18π м2, а его центральный угол равен 40°. Найдите радиус сектора. Вариант II 1. Длина окружности равна С. Найдите площадь ограниченного ею круга. 2. Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 25 и 24 см. 3. Найдите площадь кругового сектора радиуса 3 см, если его центральный угол равен 20°. 4. Площадь кругового сектора равна 10π м2, а его радиус равен 6 м. Найдите центральный угол сектора. 5. Найдите длину дуги окружности радиуса 6 дм, если ее градусная мера равна 120°. 6. Найдите радиус окружности, если длина дуги окружности равна 6π, а ее градусная мера равна 60°. II. Решение задач. 1. Решить задачу 1. Докажите, что площадь S треугольника АВС вычисляется по формуле. 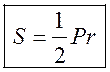 , ,где Р – периметр треугольника, r – радиус вписанной окружности. Доказательство Ads by optAd360 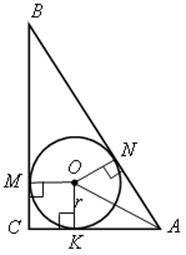 Пусть О – центр окружности, которая вписана в треугольник АВС и, следовательно, касается сторон треугольника в точках М, N и K. АОВ. *ВОС + SАОС + SОчевидно, что S = S АОС =Так как ОМ, ОN и ОK – высоты треугольников АОС, ВОС и АОВ, то S ВОС =АС · ОK, S АОВ =ВС · ОМ и S АВ · ОN. Подставив эти значения в формулу *, получим: S =(AB + BC + CA) · r =P · r. 2. Решить задачу 2. даны стороны треугольника АВС – а, b, с и площадь S. Выразить радиусы окружностей, описанной около треугольника и вписанной в него, через а, b, с и S. Решение 1) Используем результат задачи 1: S =Pr, где Р – периметр треугольника, r – радиус вписанной окружности. Р = а + b + с; 2S = r (а + b + c), отсюда: 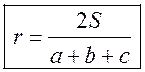 Ads by optAd360 2) Радиус R описанной окружности вычисляется по формуле: R =  – угол, противолежащий стороне а., где – угол, противолежащий стороне а., где Из формулы: S = = получим sin bc · sin =, тогда 2sin . Следовательно, R = 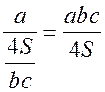 . . 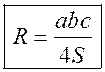 3. Решить задачу № 1099 на доске и в тетрадях. Решение Диагонали А3А7 и А4А8 четырехугольника А3А4А7А8 являются диаметрами окружности, в которую вписан данный восьмиугольник, поэтому они равны и точкой пересечения О делятся пополам. Следовательно, четырехугольник А3А4А7А8 – прямоугольник. Так как угол А3ОА4 = 45°, то согласно задаче 1059 площадь прямоугольника равна R2. 4. Решить задачу № 1105 (в) (объясняет учитель). Решение ., b = c · sin , АВ = с, ВС = а, СА = b; Р = а + b + с, r – радиус вписанной окружности. Тогда а = с · cos Пусть АВС – данный треугольник, угол С = 90°, угол В = Воспользуемся двумя формулами для вычисления площади S треугольника АВС (метод площадей): 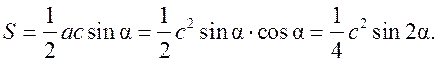 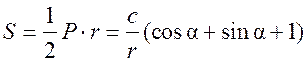 . Отсюда, получаем, r = . Отсюда, получаем, r =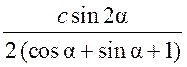 , поэтому C = 2πr = , поэтому C = 2πr =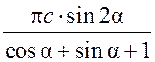 . .Ads by optAd360 – 1). + cos – 1, после несложных преобразований получаем: c = πc (sin + sin Умножив числитель и знаменатель дроби на cos 5. Решить задачу № 1117 (в). решение Применим метод площадей, то есть воспользуемся двумя формулами для вычисления площади треугольника: S = и S =ab sin – угол между ними, Р – периметр, r – радиус вписанной окружности. Получим: S =Pr, где а и b – длины сторон треугольника, и S = r · аa2 sin 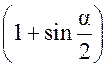 . .Отсюда находим r, а затем площадь круга: Sкруга = 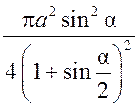 . .6. Решить задачи № 1110, 1138, 1116 (в). Примечание. решения некоторых из них полезно предварительно обсудить, а затем записать в тетрадях, остальные задачи учащиеся могут решить самостоятельно с последующей проверкой ответов или решений. III. Проверочная самостоятельная работа. Вариант I Решить задачи №№ 1125, 1129 (в), 1132 (а), 1134 (а). Вариант II Решить задачи №№ 1128, 1129 (г), 1132 (б), 1134 (б). Ads by optAd360 IV. Итоги уроков. Домашнее задание: подготовиться к контрольной работе, повторив материал пунктов 105–112 и ответив на вопросы 1–12, с. 290 учебника; решить задачи №№ 1104 (г, д), 1105 (б), 1116 (в). Контрольная работа № 3 - ДЛИНА ОКРУЖНОСТИ. ПЛОЩАДЬ КРУГА Цели: проверить умение учащихся решать задачи по изученной теме; выявить пробелы в знаниях учащихся для последующего их устранения. Ход урока I. Организация учащихся для выполнения контрольной работы. II. Выполнение работы по вариантам. Вариант I 1. Периметр правильного треугольника, вписанного в окружность, равен 45 см. Найдите сторону правильного восьмиугольника, вписанного в ту же окружность. 2. Найдите площадь круга, если площадь вписанного в ограничивающую его окружность квадрата равна 72 дм2. 3. Найдите длину дуги окружности радиуса 3 см, если ее градусная мера равна 150°. Вариант II 1. Периметр правильного шестиугольника, вписанного в окружность, равен 48 м. Найдите сторону квадрата, вписанного в ту же окружность. 2. Найдите длину окружности, если площадь вписанного в нее правильного шестиугольника равна 72 см2. 3. Найдите площадь кругового сектора, если градусная мера его дуги равна 120°, а радиус круга равен 12 см. вариант III 1. Периметр квадрата, вписанного в окружность, равен 48 см. найдите сторону правильного пятиугольника, вписанного в ту же окружность. 2. Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 3 см и 7 см. 3. Найдите площадь фигуры, ограниченной дугой окружности и стягивающей ее хордой, если длина хорды равна 4 м, а градусная мера дуги равна 60°. Вариант IV 1. Периметр правильного пятиугольника, вписанного в окружность, равен 6 дм. Найдите сторону правильного треугольника, вписанного в ту же окружность. 2. Площадь кольца, ограниченного двумя окружностями с общим центром, равна 45π м2, а радиус меньшей окружности равен 3 м. Найдите радиус большей окружности. 3. Найдите площадь фигуры, ограниченной дугой окружности и стягивающей ее хордой, если длина хорды равна 2 см, а диаметр окружности равен 4 см. Домашнее задание: повторить пункт 47 «Осевая и центральная симметрии». Ads by optAd360 Ads by optAd360 ПредыдущаяСодержаниеСледующая Начало формы
Конец формы Библиотека образовательных материалов для студентов, учителей, учеников и их родителей. Все материалы доступны по лицензии Creative Commons — «Attribution-NonCommercial» Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями. Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта. Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид. © 2014-2021 Все права на дизайн сайта принадлежат С.Є.А. Отображение плоскости на себя. Понятие движения - ДВИЖЕНИЯ Цели: ввести понятие отображения плоскости на себя и понятие движения; напомнить построение фигур относительно центра и относительно оси; рассмотреть свойства осевой и центральной симметрии и закрепить их знание при решении задач. Ход уроков I. Анализ контрольной работы. 1. Указать ошибки, сделанные учащимися при решении задач. 2. Решить на доске задачи, вызвавшие затруднения у учащихся. II. Повторение ранее изученного материала. 1. Повторение понятий точек, симметричных относительно данной прямой (оси симметрии), и точек, симметричных относительно данной точки (центра симметрии). 2. В ходе повторения нужно подвести учащихся к понятию сохранения расстояния между точками. Этой цели служат следующие задачи: 1) Для каждого из случаев, представленных на рисунке 1, а, б, в, постройте точки А1 и В1, симметричные точкам А и В относительно прямой l. 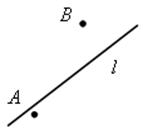 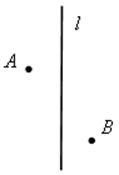  а б в Рис. 1 2) Существует ли на плоскости такая точка, для которой нет симметричной точки относительно данной прямой? 3) Докажите, что в каждом из рассмотренных в задаче 1 случаев А1В1 = АВ. 4) Постройте точки А1 и В1, симметричные А и В относительно точки О, если: а) точка О лежит на отрезке АВ; б) точка О не лежит на прямой АВ. 5) Существует ли такая точка плоскости, для которой нет точки, симметричной относительно данной точки? 6) Докажите, что в каждом из рассмотренных в задаче 4 случаев А1В1 = АВ. III. Изучение нового материала. 1. Ввести понятие отображения плоскости на себя и проиллюстрировать его примерами осевой и центральной симметрий. Ads by optAd360 Важно подчеркнуть, что при отображении плоскости на себя выполняются два условия: 1) каждой точке плоскости ставится в соответствие какая-то одна точка плоскости и 2) каждая точка плоскости оказывается поставленной в соответствие какой-то точке плоскости. Нужно показать, что в случаях осевой и центральной симметрий выполняются оба условия. В качестве контрпримера можно привести соответствие между точками плоскости, при котором каждой точке плоскости ставится в соответствие ее ортогональная проекция на данную прямую. В этом случае нарушено второе условие отображения плоскости на себя: не каждая точка плоскости оказывается сопоставленной какой-то точке, а именно любая точка, не лежащая на данной прямой, не будет сопоставлена никакой точке плоскости (плоскость отображается не на себя, а на данную прямую). 2. Решить задачи № 1148 (а) и №1149 (а). 3. Ввести понятие движения, опираясь на задачи 3 и 6, рассмотренные в начале урока. В качестве примера отображения плоскости на себя, не являющегося движением, то есть не сохраняющего расстояния между точками, можно рассмотреть центральное подобие (гомотетию) с коэффициентом 2; учащиеся сами могут доказать, что при таком отображении расстояния между точками увеличиваются в два раза. 4. Решить задачу № 1153 для усвоения понятия, а затем по заранее подготовленному рисунку 2 решить следующую задачу: «При движении плоскости точка А переходит в точку М. В какую из обозначенных на рисунке 2 точек может отобразиться при этом движении точка В?». 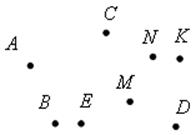 Ads by optAd360 Рис. 2 5. Доказать, что осевая и центральная симметрии являются движениями. После этого рассматривается теорема о том, что при движении отрезок отображается на отрезок, и следствие из нее. В ходе доказательства теоремы полезно акцентировать внимание учащихся на том, что доказательство состоит из двух частей: во-первых, доказывается, что каждая точка Р данного отрезка МN отображается в некоторую точку Р1 отрезка М1N1 и, во-вторых, что в каждую точку Р1 отрезка М1N1 переходит какая-то точка Р данного отрезка МN. IV. Закрепление изученного материала. 1. Разобрать решение задачи № 1150. 2. Решить задачи №№ 1151, 1152 (а, б), 1158. 3. Хотя пункт 115* не является обязательным, учащиеся должны знать, что понятия наложения и движения эквивалентны, а значит, при движении любая фигура переходит в равную ей фигуру. Для лучшего усвоения материала этого пункта полезно обсудить решение задачи № 1156 и решить задачи №№ 1154, 1157, 1155. V. Итоги уроков. Домашнее задание: изучить материал пунктов 113–114; ответить на вопросы 1–13, с. 303 учебника; решить задачи №№ 1149 (б), 1148 (б), 1159, 1160, 1161, 1174. Основные требования к учащимся. в результате изучения параграфа учащиеся должны уметь объяснить, что такое отображение плоскости на себя; знать определение движения плоскости; уметь доказывать, что осевая и центральная симметрии являются движениями и что при движении отрезок отображается на отрезок, а треугольник – на равный ему треугольник; уметь решать задачи типа задач №№ 1152, 1159, 1161. Параллельный перенос - ДВИЖЕНИЯ Цели: ввести понятие параллельного переноса, доказать, что параллельный перенос является движением; научить решать задачи с использованием параллельного переноса. Ход урока I. Проверка изученного материала. 1. По таблицам «Центральная симметрия» и «Осевая симметрия» повторить построение геометрических фигур и свойства движения. 2. Ответить на вопросы 1–13 на с. 303. II. Изучение нового материала. Теоретический материал пункта 116 можно изложить в виде лекции, используя таблицу «Параллельный перенос». 1. Определение параллельного переноса. 2. Доказательство утверждения, что параллельный перенос является движением (рис. 329). 3. При параллельном переносе прямая отображается на параллельную ей прямую или сама на себя. Отсюда следует простой способ построения образов прямых и отрезков при параллельном переносе. 4. Построение образов прямых и отрезков при параллельном переносе учителем на доске, а учащимися в тетрадях. III. Закрепление изученного материала. 1. Решить задачи № 1162 и №1163 (б) на доске и в тетрадях. 2. Решить задачу № 1164. IV. Итоги урока. Домашнее задание: изучить материал пункта 116; решить задачи №№ 1163 (а), 1165. Принести циркули и транспортиры. Поворот – ДВИЖЕНИЯ (2 урока) Цели: ввести понятие поворота; доказать, что поворот является движением; научить учащихся построению геометрических фигур при повороте фигуры на данный угол. Ход уроков I. Проверочная работа (15 мин). На отдельных листочках учащиеся выполняют построения, а затем сдают учителю работы на проверку. Задачи. 1) Даны треугольник МNK и точка О. Постройте фигуру F, на которую отображается треугольник MNK при центральной симметрии с центром О. 2) Даны прямая l и четырехугольник РМЕС. Постройте фигуру F, на которую отображается данный четырехугольник при осевой симметрии с осью l. 3) Даны окружность с центром О и прямая l. Постройте фигуру F, на которую отображается данная окружность при осевой симметрии с осью l. II. Объяснение нового материала (лекция). Теоретический материал пункта «Поворот» можно изложить в форме лекции. (рис. 330).1. Определение поворота плоскости вокруг точки О на угол 2. Поворот вокруг точки О по часовой стрелке или против часовой стрелки (использовать таблицу «Поворот»). 3. Доказательство утверждения, что поворот является движением, то есть отображением плоскости на себя, сохраняющим расстояния (рис. 331). III. Закрепление изученного материала. 1. Решить задачу № 1166 на доске и в тетрадях. Примечание. В ходе решения этой задачи полезно подчеркнуть, что поворот вокруг точки на 180° по часовой стрелке совпадает с поворотом вокруг этой же точки на 180° против часовой стрелки и является центральной симметрией. 2. Решить задачи № 1167 и №1169 (учащиеся могут выполнить эти задания самостоятельно с последующим обсуждением). 3. Полезно предложить учащимся самостоятельно изучить решение задачи № 1171 (а), приведенное в учебнике, выполнить необходимые построения, а затем можно обсудить это решение. Важно подчеркнуть, что решение рассмотренной задачи дает еще один способ построения прямой, на которую отображается данная прямая при повороте вокруг данной точки. Ads by optAd360 4. Рассмотреть с учащимися следующие задачи: 1) Через центр квадрата проведены две взаимно перпендикулярные прямые. Докажите, что их точки пересечения со сторонами квадрата являются вершинами другого квадрата. 2) Докажите, что при повороте правильного треугольника АВС вокруг вершины А на 60° либо вершина В переходит в вершину С, либо вершина С переходит в вершину В. 5. Решить задачу № 1170 (б). IV. Самостоятельная работа (обучающего характера). Вариант I 1. В трапеции АВСD боковые стороны АВ и СD равны. 1) Постройте отрезок СА1, на который отображается сторона АВ при параллельном переносе на вектор . 2) Найдите площадь треугольника А1СD, если АD = 10 см, ВС = 4 см, АВ = 6 см. 2. Докажите, что правильный шестиугольник при повороте на 60° вокруг своего центра отображается на себя. Вариант II 1. Точка М – середина стороны АС треугольника АВС. 1) Постройте отрезок МВ1, на который отображается сторона АВ при параллельном переносе на вектор . 2) Найдите периметр треугольника МDС, где D – точка пересечения отрезков ВС и МВ1, если периметр треугольника АВС равен 12 м. 2. Докажите, что правильный пятиугольник при повороте на 72° вокруг своего центра отображается на себя. Ads by optAd360 V. Итоги уроков. Домашнее задание: изучить материал пунктов 116–117; ответить на вопросы 14–17, с. 304 учебника; решить задачи № 1168, 1170 (а), 1171 (б), 1183; подготовиться к устному опросу по карточкам, повторив материал пунктов 113–114. Решение задач - урок 6 - ДВИЖЕНИЯ Цели: закрепить знания учащихся по теме «Движения», развивать умение решать задачи с применением движений. Ход урока I. Устный опрос учащихся по карточкам. Карточка 1 1. Объясните, что такое отображение плоскости на себя. 2. Докажите, что параллельный перенос является движением. 3. Точка М – середина стороны ВС правильного треугольника АВС, точки N и K симметричны точке М относительно прямых АВ и АС. Докажите, что NK АМ. Карточка 2 1. Что такое движение плоскости? 2. Докажите, что осевая симметрия является отображением плоскости на себя. 3. На окружности с центром О и радиусом r отмечена точка А. Постройте окружность, на которую отображается данная окружность при повороте вокруг точки А на 60° по часовой стрелке. найдите длину отрезка, соединяющего точки пересечения данной и построенной окружностей. Карточка 3 1. На какую фигуру отображается при движении отрезок? 2. Докажите, что центральная симметрия является движением. 3. Дан равнобедренный треугольник АВС с основанием ВС. Постройте точки D и Е, на которые отображаются точки А и С при параллельном переносе на вектор , и докажите, что АЕ = DВ. Карточка 4 1. На какую фигуру отображается при движении треугольник? 2. Докажите, что поворот плоскости вокруг точки является движением. 3. Точка пересечения диагоналей четырехугольника АВСD является его центром симметрии. Докажите, что АВСD – параллелограмм. II. Решение задач. 1. На этих уроках рекомендуется рассмотреть простые задачи, причем большинство из них целесообразно решать в ходе обсуждения с учащимися. Это относится к задачам №№ 1172, 1173, 1177, 1180. 2. Полезно обсудить и решения задач № 1176, №1178. 3. Задачи №№ 1174, 1175, 1181 и 1182 можно предложить учащимся решить самостоятельно, а затем обсудить полученные решения. Решения Ads by optAd360 1) задача № 1172. Поскольку точки А и В отображаются на себя, то и прямая АВ отображается на себя. Пусть М – произвольная точка прямой АВ. Она отображается в некоторую точку М1, также лежащую на прямой АВ. По определению движения АМ = АМ1, ВМ = ВМ1. Допустим, что точка М1 не совпадает с точкой М. Тогда из первого равенства следует, что точка А – середина отрезка ММ1, а из второго равенства, что точка В также середина отрезка ММ1. Значит, точки А и В совпадают, что противоречит условию задачи. Следовательно, наше предположение неверно, то есть точки М и М1 совпадают. Итак, любая точка прямой АВ отображается на себя. 2) Задача № 1173. Пусть g – данное движение, а е – тождественное отображение плоскости на себя, то есть отображение, при котором каждая точка плоскости и, в частности, каждая вершина треугольника АВС отображается на себя. Ясно, что е – движение, поэтому согласно задаче № 1155 движения g и е совпадают, и, значит, движение g является тождественным отображением плоскости на себя. 3) Задача № 1180. Рассмотрим поворот вокруг точки О на 120° в направлении обхода по дуге АВС от точки А к точке С. Так как АОВ = ВОС = СОА = 120° и ОА = ОВ = ОС, то при этом повороте точка А отображается в точку В, точка В – в точку С, точка С – в точку А. Аналогично при этом же повороте точки А1, В1, С1 отображаются соответственно в точки В1, С1 и А1. Следовательно, прямая АА1 отображается на прямую ВВ1, прямая ВВ1 – на прямую СС1, прямая СС1 – на прямую АА1. Отсюда следует, что если прямая АА1 проходит через точку О, то прямые ВВ1 и СС1 также проходят через эту точку. Если же прямая АА1 не проходит через точку О, то и прямые ВВ1 и СС1 не проходят через эту точку и, попарно пересекаясь, образуют некоторый треугольник МNР. Ясно, что при рассматриваемом повороте точка М пересечения отрезков АА1 и ВВ1 отображается в точку пересечения отрезков ВВ1 и СС1. Аналогично точка N отображается в точку Р пересечения отрезков СС1 и АА1, а точка Р – в точку М. Следовательно, МN = NP = PМ, то есть треугольник МNР – равносторонний. Ads by optAd360 Домашнее задание: подготовиться к контрольной работе: повторить материал пунктов 113–117 и ответить на вопросы 1–17, с. 303–304 учебника; решить задачи №№ 1219, 1220, 1221, 1222. |

