геометрия. геометрия 9 класс. Ход уроков I. Повторение ранее изученного материала
 Скачать 0.76 Mb. Скачать 0.76 Mb.
|
|
Уравнение линии на плоскости. Уравнение окружности - МЕТОД КООРДИНАТ Цели: познакомить учащихся с понятием уравнения линии на плоскости; вывести уравнение окружности и научить записывать уравнение окружности. Ход урока I. Математический диктант (10–15 мин). Вариант I 1. Найдите координаты середины отрезка AB, если A (–2; 3), B (6; –3). 2. Найдите длину отрезка EH, если E (–3; 8), H (2; –4).. 3. Какая фигура состоит из множества всех точек плоскости, каждая из которых равноудалена от двух данных точек? 4. Принадлежит ли точка A (–6; 2) графику функции y = – 0,5x? 5. Функция задана уравнением y = 2x – 3. Какая линия служит графиком этой функции? 6. На окружности радиуса 7 см даны точки А и В, расстояние между которыми равно 13 см. лежит ли центр окружности на прямой АВ? 7. Вершины треугольника ABC имеют следующие координаты: А (8; –3); В (5; 1); С (12; 0). Докажите, что B = C. Вариант II 1. Найдите координаты середины отрезка CD, если C (3; –4), D (–3; 6). 2. Найдите длину отрезка KB, если K (–6; –3), B (2; 3).. 3. Прямая l является серединным перпендикуляром к основанию AB треугольника ABC и проходит через вершину C. Определите вид треугольника ABC. 4. Принадлежит ли точка В (2; –8) графику функции y = – 4x? 5. Функция задана уравнением y = 5 – x. Какая линия служит графиком этой функции? 6. Какой фигурой является множество точек, равноудаленных от данной точки? 7. Вершины четырехугольника ABCD имеют следующие координаты: А (–3; –1); В (1; 2); С (5; –1), D (1; –4). Докажите, что этот четырехугольник – ромб. II. Объяснение нового материала. 1. Разобрать пятое задание диктанта, обратив внимание учащихся на то, что им уже известны графики некоторых функций. В частности, графиком линейной функции y = kx + b является прямая линия, а уравнение y = kx + b называется уравнением этой прямой. 2. Вспомнить уравнения параболы и гиперболы и их графики. Ads by optAd360 3. Понятие уравнения произвольной линии дается в ознакомительном плане. При этом важно добиться понимания учащимися следующего: чтобы установить, что данное уравнение является уравнением данной линии, нужно доказать, что: 1) координаты любой точки линии удовлетворяют данному уравнению и 2) координаты любой точки, не лежащей на данной линии, не удовлетворяют этому уравнению. 4. Введение уравнения окружности радиуса r с центром С в заданной прямоугольной системе координат (рис. 286). (x – x0)2 + (y – y0)2 = r2, где C (x0; y0). Уравнение окружности радиуса r с центром в начале координат О (0; 0) имеет вид: x2 + y2 = r2. 5. Не любое уравнение второй степени с двумя переменными задает окружность. Например, уравнение 4х2 + у2 = 4 в прямоугольной системе координат не окружность, а эллипс (с этой фигурой учащиеся знакомились в курсе черчения), уравнение х2 + у2 = 0 задает единственную точку – начало координат, а уравнению х2 + у2 = –4 не удовлетворяют координаты ни одной точки, поэтому это уравнение не задает никакой фигуры. III. Закрепление изученного материала (решение задач). 1. решить задачу № 959 (а, б, д). 2. Устно решить задачу № 960. 3. решить задачу № 961 на доске и в тетрадях. 4. решить задачу № 964 на доске и в тетрадях. Решение а) x = 3, тогда (3 – 3)2 + (y – 5)2 = 25; y2 – 10y + 25 = 25; y2 – 10y = 0; y ∙ (y – 10) = 0; y = 0 или y = 10. Точки А (3; 0) и В (3; 10). б) y = 5, тогда (x – 3)2 + (5 – 5)2 = 25; x2 – 6x + 9 = 25; Ads by optAd360 x2 – 6x – 16 = 0; x1 = 8; x2 = –2; точки С (–2; 5) и D (8; 5). 5. Решить задачу № 966 (в, г). 6. Разобрать решение задачи по учебнику на с. 243. IV. Итоги урока. Домашнее задание: изучить материал пунктов 90, 91; вопросы 15–17; решить задачи №№ 962, 963, 965, 966 (а, б), 1000. Уравнение окружности. Решение задач - МЕТОД КООРДИНАТ Цели: закрепить знания учащихся в ходе решения задач; развивать логическое мышление учащихся. Ход урока I. Проверка домашнего задания. 1. Результаты математического диктанта. Указать ошибки, сделанные учащимися. 2. На доске один ученик выводит уравнение окружности. 3. С остальными учащимися проверяется решение домашних задач. II. Выполнение упражнений. 1. Решить задачу. Напишите уравнение окружности с центром в точке А (0; 4), проходящей через точку D (–6; –4). Решение Центр окружности имеет координаты А (0; 4). Найдем радиус окружности r = AD по формуле: d =. r = AD = Значит, искомое уравнение окружности имеет вид: (x – 0)2 + (y – 4)2 = 102; x2 + (y – 4)2 = 100. Ответ: x2 + (y – 4)2 = 100. 2. Решить задачу № 969 (а) на доске и в тетрадях. Решение Диаметр окружности MN = 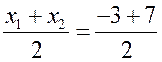 = 2; y = = 2; y =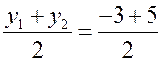 = 1. Центр В (2; 1). Напишем уравнение окружности: (x – 2)2 + (y – 1)2 = 41. = 1. Центр В (2; 1). Напишем уравнение окружности: (x – 2)2 + (y – 1)2 = 41.3. Решить задачу № 970. Решение Центр окружности лежит на оси абсцисс, то координаты центра D (x; 0); радиус равен r = 5. Окружность проходит через точку А (1; 3), тогда AD = r, поэтому (x – 1)2 + (3 – 0)2 = r2 = 52, (x – 1)2 + 9 = 25; x2 – 2x – 15 = 0; x1 = –3; x2 = 5. Ads by optAd360 Следовательно, координаты центров окружностей D1 (–3; 0) и D2 (5; 0). Существует две таких окружности: (x + 3)2 + y2 = 25 и (x – 5)2 + y2 = 25. 4. Решить задачу № 971 на доске и в тетрадях. Решение Центр окружности лежит на оси ординат, значит, координаты центра С (0; y). По условию, окружность проходит через точки А (–3; 0) и В (0; 9), значит, расстояния АС = ВС = r радиусу: (0 + 3)2 + (y – 0)2 = (0 – 0)2 + (y – 9)2; 9 + y2 = y2 – 18y + 81; 18y = 72; y = 4. Следовательно, центр окружности имеет координаты С (0; 4). Найдем радиус окружности: r2 = AC2 = (0 + 3)2 + (4 – 0)2 = 9 + 16 = 25; r = 5. Напишем уравнение окружности: (x – 0)2 + (y – 4)2 = 52; то есть x2 + (y – 4)2 = 25. 5. Решить задачу № 1002(а) на доске и в тетрадях (решение задачи объясняет учитель). Решение Координаты точек А, В и С должны удовлетворять уравнению окружности (x – a)2 + (y – b)2 = r2. Подставив в это уравнение координаты данных точек, получим систему трех уравнений относительно неизвестных a, b и r : 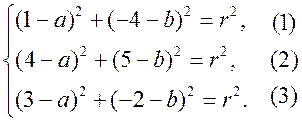 Вычтем из уравнения (1) сначала уравнение (2), а затем уравнение (3). Получим систему двух линейных уравнений с неизвестными a и b, которую учащиеся могут решить самостоятельно 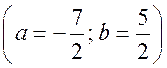 . Подставив эти значения в любое из уравнений, например, в уравнение (1), находим значение r2 и записываем искомое уравнение: . Подставив эти значения в любое из уравнений, например, в уравнение (1), находим значение r2 и записываем искомое уравнение: 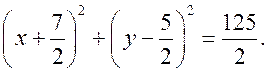 Ads by optAd360 III. Итоги урока. Домашнее задание: повторить материал пунктов 86–91; решить задачи №№ 969 (б), 981 (есть решение в учебнике), 1002 (б). Уравнение прямой - МЕТОД КООРДИНАТ Цели: вывести уравнение прямой и показать, как можно использовать это уравнение при решении геометрических задач; развивать логическое мышление учащихся. Ход урока I. Самостоятельная работа (контролирующая, 10–15 мин). Вариант I Решить задачи № 959 (г), 968, 960 (б). Вариант II Решить задачи № 959(в), 967, 960 (в). II. Изучение нового материала. 1. Уравнением любой прямой в прямоугольной системе координат является уравнение первой степени с двумя переменными (уравнение прямых, параллельных осям координат, также можно считать уравнением с двумя переменными, например, уравнение x = x0 можно записать в виде x + 0y = x0) и, наоборот, любое уравнение первой степени с двумя переменными задает прямую. 2. Вывести уравнение данной прямой l в заданной прямоугольной системе координат (рис. 287): ax + by + c = 0. 3. Вывести уравнение прямой l, проходящей через точку M0 (x0; y0) и параллельной оси ОX (рис. 288) y = y0. 4. Ось OX имеет уравнение y = 0, а ось OY – уравнение x = 0. III. Закрепление изученного материала (решение задач). 1. Учитель объясняет решение задачи. напишите уравнение прямой, проходящей через две данные точки Р (2; 1) и Q (–3; –1). Решение Уравнение прямой PQ имеет вид ax + by + c = 0. Так как точки P и Q лежат на прямой PQ, то их координаты удовлетворяют этому уравнению: 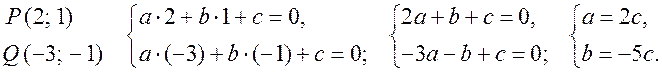 2cx – 5cy + c = 0 |: c 0, тогда прямая PQ задана уравнением 2x – 5y + 1 = 0. Ответ: 2x – 5y + 1 = 0. 2. Самостоятельно по учебнику учащиеся разбирают решение задачи № 972 (а), с. 245. 3. Решить задачу № 973 на доске и в тетрадях. Ads by optAd360 4. Решить задачу № 975. Решение Пересечение прямой с осью OX: y = 0, тогда 3x – 4 ∙ 0 + 12 = 0; 3x = –12; x = –4; точка А (–4; 0); пересечение прямой с осью OY: x = 0, тогда 3 ∙ 0 – 4y + 12 = 0; –4y = –12; y = 3; точка В (0; 3). 5. Решить задачу № 976 (повторить при решении способ сложения систем уравнений): 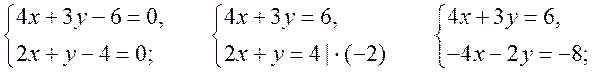 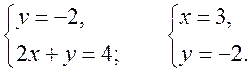 Точка пересечения прямых D (3; –2). Ответ: (3; –2). 6. Решить задачу № 977. Решение Прямая, проходящая через точку М (2; 5) и параллельная оси OX, имеет вид: y = 5; прямая, параллельная оси OY, записывается уравнением: х = 2. 7. Самостоятельное решение учащимися задачи № 978. 8. Решить устно задачи. 1) Окружность задана уравнением (x – 1)2 + y2 = 9. Назвать уравнение прямой, проходящей через ее центр и параллельной оси ординат. Решение Центр О (1; 0) и параллельная оси OY прямая x = 1. Ads by optAd360 2) Окружность задана уравнением (x + 1)2 + (y – 2)2 = 16. Назвать уравнение прямой, проходящей через ее центр и параллельной оси абсцисс. Решение Центр А (–1; 2); прямая y = 2 параллельна оси OX. IV. Итоги урока. Домашнее задание: повторить материал пунктов 86–91; изучить материал пункта 92; вопросы 1–21, с. 249; решить задачи №№ 972 (б), 979; записать в тетрадях и разобрать решение задачи № 984 (с. 248 учебника); подготовиться к устному опросу по карточкам. Решение задач - МЕТОД КООРДИНАТ (2 урока) Цели: закрепление знаний и умений учащихся по материалу главы; повторение и обобщение изученного материала; развитие логического мышления учащихся при решении задач. Ход уроков I. математический диктант (15 мин). Вариант I 1. Лежит ли точка А (2; –1) на окружности, заданной уравнением (х – 2)2 + (у – 3)2 = 25? 2. Напишите уравнение окружности, если ее центр – точка (4; 5), а радиус равен 3. 3. Напишите уравнение прямой, проходящей через точку М (3; –2) и параллельной оси ординат. 4. Напишите уравнение окружности с центром в начале координат, если она проходит через точку С (–2; 3). 5. Напишите уравнение прямой, проходящей через две точки М (–2; –1) и N (3; 1). 6. Найдите длину вектора (–12; 5). 7. Найдите координаты середины отрезка PQ, если P (5; –3); Q (3; –7). 8. Найдите координаты вектора , если А (2; –5), В (–3; 4). Вариант II 1. Лежит ли точка А (2; –1) на прямой, заданной уравнением 2х – 3у – 7 = 0? 2. Напишите уравнение окружности, если ее центр – точка (4; 5), а радиус равен 2. 3. Напишите уравнение прямой, проходящей через точку N (–2; 3) и параллельной оси абсцисс. 4. Напишите уравнение прямой, проходящей через начало координат и точку D (3; –2). 5. Напишите уравнение окружности с центром в точке Р (–2; –1), если она проходит через точку Q (1; 3). 6. Найдите расстояние между точками А (–1; 3) и В (2; –1). 7. Найдите координаты вектора , равного сумме векторов и , если (–12; 5), (7; –3). 8. Найдите координаты вектора , если С (–1; 6), D (3; –2). II. решение задач. 1. Устно решить задачу № 933. Ads by optAd360 2. решить устно задачу № 943 по готовому чертежу на доске. Решени. Из прямоугольного треугольника АОС по теореме Пифагора находим AC = ; из прямоугольного треугольника ВОС находим по теореме Пифагора BC = . 3. Разобрать по учебнику и записать решение задачи № 953 в тетради (подчеркнуть, что теорема: «Сумма квадратов всех сторон параллелограмма, ромба, прямоугольника, квадрата равна сумме квадратов его диагоналей» – используется часто при решении задач по стереометрии в 10 и 11 классах) (рис. 283 учебника). 4. решить задачи №№ 991, 996, 997, 999 на доске и в тетрадях. III. Опрос учащихся по теоретическому материалу. Примерные варианты карточек для устного опроса учащихся. Вариант I 1. Сформулируйте теорему о разложении вектора по двум данным неколлинеарным векторам. 2. Выведите формулы координат середины отрезка по координатам его концов. 3. Напишите уравнение окружности с центром в точке В (4; 0), если она проходит через точку А (7; 4). вариант II 1. Сформулируйте правило нахождения координат разности двух векторов. 2. Выведите формулу для вычисления длины вектора по его координатам. 3. Напишите уравнение прямой, проходящей через две точки А (–3; –3) и В (3; 5). Ads by optAd360 Вариант III 1. Сформулируйте правило нахождения координат произведения вектора на число по заданным координатам вектора. 2. Выведите уравнение окружности данного радиуса с центром в данной точке, заданной координатами. 3. Найдите координаты середины отрезка АВ, если даны координаты его концов А (–3; 4) и В (3; –6). Вариант IV 1. Сформулируйте утверждение о разложении произвольного вектора по координатным векторам. 2. Выведите уравнение прямой l в прямоугольной системе координат, если l является серединным перпендикуляром к отрезку с концами А (х1; у1) и В (х2; у2). 3. Найдите расстояние между точками М (2; –1) и N (5; –3). IV. решение задач. 1. Решить задачу № 1004. Решени. Достаточно доказать, что данные прямые не имеют ни одной общей точки. Для этого запишем уравнения данных прямых так: y = 2x + и y = 2x – 3. Ясно, что эта система несовместна, то есть нет чисел х, у, удовлетворяющих этим двум уравнениям. Геометрически это означает, что данные прямые не имеют ни одной общей точки и, значит, они параллельны. 2. Решить задачу № 1007. Решени. Пусть ОАВС – данная трапеция с основаниями ОА = а и ВС = b (пусть а > b) и высотой h. Введем прямоугольную систему координат ОХY так, чтобы точка А лежала на положительной полуоси ОХ, а прямая ВС пересекала положительную полуось ОY. В этой системе координат вершины трапеции будут иметь координаты О (0; 0), А (а; 0), С (с; h) и В (с + b; h), где с – некоторое число. Находим координаты середин М и N диагоналей трапеции и вычисляем расстояние между ними: MN = . Таким образом, MN = (OA – BC). Ads by optAd360 3. Решить задачу № 1010 (а). Решени. Введем систему координат так, чтобы точки А и В имели координаты А (0; 0), В (а; 0), где а = АВ. Пусть М (х; у) – произвольная точка. Условие 2АМ2 – ВМ2 = 2АВ2, записанное в координатах, дает уравнение искомого множества. Оно приводится к виду: (х + а)2 + у2 = (2а)2. Этим уравнением задается окружность радиуса 2а с центром в точке (–а; 0), то есть в точке, симметричной точке В относительно точки А. V. Итоги уроков. Домашнее задание: повторить материал пунктов 86–92; пунктов 66–67 (материал 8 класса); решить задачи №№ 1010 (б), 990, 958, 944, 945, 998. Контрольная работа № 1 - МЕТОД КООРДИНАТ Цели: проверить знания, умения и навыки учащихся по усвоению и применению изученного материала. Ход урока I. Организация учащихся на выполнение работы. II. Выполнение работы по вариантам. Вариант I 1. Точки E и F лежат соответственно на сторонах AD и BC параллелограмма ABCD; AE = ED, BF : FC = 4 : 3. Выразите вектор через векторы и . 2. Найдите координаты вектора , если 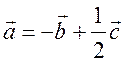 , (3; –2), ( –6; 2). , (3; –2), ( –6; 2).3. Боковые стороны прямоугольной трапеции равны 15 см и 17 см, средняя линия равна 6 см. Найдите основания трапеции. Вариант II 1. Точки K и M лежат соответственно на сторонах AB и CD параллелограмма ABCD; AK = KB, CM : MD = 2 : 5. Выразите вектор через векторы и . 2. Найдите координаты вектора , если , (–3; 6), (2; –2). 3. Один из углов прямоугольной трапеции равен 120°, бóльшая боковая сторона равна 20 см, средняя линия равна 7 см. Найдите основания трапеции. Вариант III 1. Точки P и O лежат соответственно на сторонах AD и BC параллелограмма ABCD; BP = PC, AO : OD = 3 : 2. Выразите вектор через векторы и . 2. Найдите координаты вектора , если 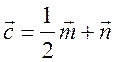 , (6; –2), (1; –2). , (6; –2), (1; –2).3. Основание и средняя линия прямоугольной трапеции равны соответственно 15 см и 12 см, а меньшая боковая сторона равна 8 см. Найдите вторую боковую сторону трапеции. Вариант IV 1. Точки H и T лежат соответственно на сторонах AВ и CD параллелограмма ABCD; CT = TD, AH : HB = 5 : 3. Выразите вектор через векторы и . Ads by optAd360 2. Найдите координаты вектора , если 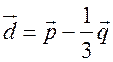 , (2; 3), (9; –9). , (2; 3), (9; –9).3. Средняя линия прямоугольной трапеции равна 9 см, а бóльшая боковая сторона равна 24 см. Один из углов, прилежащих к боковой стороне, в два раза больше другого. Найдите основания трапеции. III. Итоги урока. Домашнее задание: повторить материал пунктов 76–87; ответить на вопросы 1–8, с. 249. |
