геометрия. геометрия 9 класс. Ход уроков I. Повторение ранее изученного материала
 Скачать 0.76 Mb. Скачать 0.76 Mb.
|
|
Измерительные работы - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА Цель: познакомить учащихся с измерительными работами на местности, основанными на использовании теорем синусов и косинусов. Ход урока I. Проверка опорных знаний учащихся. Учащиеся отвечают на вопросы 2–10 на странице 271 учебника. II. работа по учебнику. 1. Тригонометрические формулы используются при проведении различных измерительных работ на местности. В 8 классе учащиеся определяли высоту предмета и расстояние до недоступной точки на основе теоремы подобия треугольников. В 9 классе эти же задачи решают с применением тригонометрических функций. 2. Учащиеся самостоятельно читают материал пункта 100 учебника. 3. Обсуждение прочитанного материала, используются рисунки 295 и 296 учебника. III. Решение задач. 1. Решить задачу № 1036 по рисунку 298. 2. Решить задачу № 1037 (использовать рисунок 296 учебника). 3. Решить задачу № 1038 по рисунку 299. IV. Итоги урока. Домашнее задание: повторить материал пунктов 93–100; решить задачи № 1034, 1064. Решение задач - урок 3 - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА Цели: систематизировать, повторить и обобщить изученный материал; научить применять полученные знания к решению задач. Ход урока I. Повторение и обобщение изученного материала. 1. Сформулировать теорему о площади треугольника. 2. Сформулировать теорему синусов. 3. Сформулировать теорему косинусов. 4. Объяснить применение теоремы косинусов при решении треугольников. 5. В какой задаче на решение треугольников можно применять только теорему синусов? 6. Рассказать решение задачи по нахождению высоты предмета и расстояния до недоступной точки с помощью тригонометрических функций. 7. Формулы приведения (записать на доске). II. Решение задач. 1. Решить задачу № 1059 на доске и в тетрадях. Пусть АВСD – выпуклый четырехугольник, О – точка пересечения его диагоналей, .AOB = Тогда SАВСD = SАОВ + SВОС + SСОD + SАОD. и АС = АО + ОС, ВD = ВО + ОD, получаем.) = sin Найдем площадь каждого из четырех треугольников, пользуясь теоремой о площади треугольника. Учитывая, что sin (180° – SАВСD = .AC ∙ BD ∙ sin 2. Решить задачу № 1063. Решение SАВС = SАВD + SАСD или воспользуемся формулой площади треугольника: =bc ∙ sin xc ∙ sin + xb ∙ sin , где x = AD. = 2sinОтсюда, учитывая, что sin ∙ cos , находим х: х = 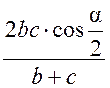 . .III. Самостоятельная работа контролирующего характера. Ads by optAd360 Вариант I Решить задачи №№ 1060 (а); 1058 (б); 1061 (а). Вариант II Решить задачи №№ 1060 (б); 1058 (а); 1061 (б). IV. Итоги урока. Домашнее задание: повторить тему «Векторы», материал пунктов 76–85 и 86–89; решить задачи №№ 1024, 1035. Угол между векторами. Скалярное произведение векторов - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА Цели: познакомить учащихся с понятием угла между векторами; ввести скалярное произведение векторов; рассказать о применении скалярного произведения векторов в физике, механике; развивать логическое мышление учащихся. Ход урока I. Математический диктант (15 мин). Вариант I 1. Диагонали параллелограмма АВСD пересекаются в точке О. какие векторы коллинеарные вектору ? 2. Диагонали параллелограмма АВСD пересекаются в точке О. Какие векторы сонаправлены с вектором ? 3. Диагонали параллелограмма АВСD пересекаются в точке О. Какие векторы равны вектору ? 4. При каком условии 5. Известно, что = 3, = 4. Найдите , если АОВD – прямоугольник. 6. В треугольнике СDЕ DЕ = 5, СЕ = 4, угол С = 45°. Найдите сторону DЕ. 7. В треугольнике КLM КL = LМ = 5, КМ = 6. Найдите косинус угла L. 8. В треугольнике ОРQ угол О = 60°, угол Р = 75°, ОР = 8. Найдите сторону РQ. Вариант II 1. Диагонали ромба КLМР пересекаются в точке Т. Какие векторы коллинеарные вектору ? 2. Диагонали ромба КLМР пересекаются в точке Т. какие векторы сонаправлены с вектором ? 3. Диагонали ромба КLМР пересекаются в точке Т. Какие векторы равны вектору ? 4. При каком условии 5. Известно, что точки С и D лежат соответственно на осях ОХ и ОY прямоугольной системы координат. Найдите 6. В треугольнике АВС АВ = ВС = 8, АС = 4. Найдите косинус угла А. 7. В треугольнике ВСD ВС = 6, угол В = 75°, угол С = 45°. Найдите сторону ВD. 8. В треугольнике DЕF DЕ = 6, ЕF = 7, угол Е = 30°. Найдите сторону DF. Ads by optAd360 II. Объяснение нового материала. 1. Ввести понятие угла между векторами и (рис. 300 и таблица). между векторами2. Угол и не зависит от выбора точки О, от которой откладываются векторы и . 3. Угол между сонаправленными векторами считается равным нулю. 4. Обозначение угла между векторами: . 5. Определение углов между векторами на рисунке 301. 6. Определение перпендикулярных векторов. 7. Повторить по настенным таблицам сложение и вычитание векторов, умножение вектора на число. 8. Введение еще одного действия над векторами – скалярного умножения векторов. В отличие от суммы и разности векторов скалярное произведение есть число (скаляр) – именно это и обусловило название операции. 9. В тетрадях учащиеся оформляют таблицу: скалярное произведение векторов 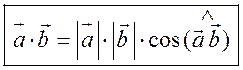 Если и , т. а) (0 ≤ < 90°) <=> ( > 0); б) (90° < ≤ 180°) <=> ( < 0); в) <=> ( = 0); г) ( = 0°) <=> Ads by optAd360 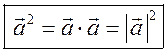 10. Скалярное произведение векторов широко используется в физике. Например, из курса механики известно, что работа А постоянной силы при перемещении тела из точки М в точку N (рис. 303) равна произведению длин векторов силы и перемещения на косинус угла между ними: III. Закрепление изученного материала. 1. Решить задачи №№ 1039 (а, б, ж, з) и 1040 (а, д, е) по готовым чертежам квадрата и ромба, заранее выполненным на доске. 2. Решить задачу № 1041 (в). Примечание. сos 135° = cos (180° – 45°) = – cos 45° = . IV. Итоги урока. Домашнее задание: изучение материалов пунктов 101 и 102; повторить материал п. 87; решить задачи №№ 1039 (в, г), 1040 (г), 1042 (а, б). Скалярное произведение в координатах. Свойства скалярного произведения векторов - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА Цели: ввести понятие скалярного произведения в координатах; изучить свойства скалярного произведения векторов и закрепить их знание при решении задач. Ход урока I. Проверочная работа (10 мин). Вариант I 1. Известно, что , где и – координатные векторы. Выпишите координаты вектора . 2. Дан вектор (0; 5). Запишите разложение вектора по координатным векторам и . 3. Даны векторы (–1; 2) и (2; 1). Найдите координаты суммы векторов и . 4. Найдите координаты вектора , если (–3; 0). 5. Даны векторы (5; 6) и (–2; 3). Найдите координаты вектора . 6. Две стороны треугольника равны 7 и 3 см, а угол между ними равен 120°. Найдите третью сторону треугольника. 7. в треугольнике АВС угол А = 45°, АВ = 2, АС = 3. Вычислите . 8. Скалярное произведение ненулевых векторов и равно нулю. Чему равен угол между векторами и ? Вариант II 1. Дан вектор (3; 0). Запишите разложение вектора по координатным векторам и . 2. Известно, что , где и – координатные векторы. Выпишите координаты вектора . 3. Найдите координаты вектора –, если (0; –2). 4. Даны векторы (2; –1) и (3; –1). Найдите координаты разности векторов и . 5. Даны векторы (–1; 9) и (3; –2). Найдите координаты вектора . 6. В треугольнике МРQ угол M = 135°; МР = 5, МQ = 2. Вычислите Ads by optAd360 7. Две стороны треугольника равны 3 и 9 м, а угол между ними равен 60°. Найдите третью сторону треугольника. 8. Чему равно скалярное произведение координатных векторов и ? II. Изучение нового материала. 1. Скалярное произведение двух векторов можно вычислить, зная координаты этих векторов. 2. Изучение теоремы о скалярном произведении векторов в координатах и свойств скалярного произведения полезно построить так, чтобы учащиеся сами проводили алгебраические преобразования. Полученные результаты можно записать в тетради и вынести в настенную таблицу: Скалярное произведение в координатах 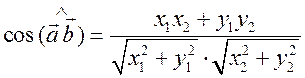 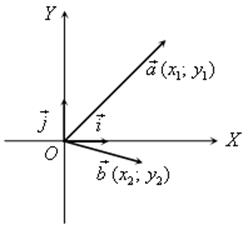 Ads by optAd360 Свойства скалярного произведения векторов: 1) ≥ 0 ( > 0 при 0). 2) ; 3) 4) III. Закрепление изученного материала. 1. Решить задачу № 1043 (объясняет учитель): Дано: = 8; = 15; АВС = 120°. Найти: . 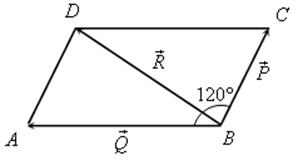 Решение Пусть ; C = 180° – 120° = 60° (сумма односторонних углов равна 180°). По теореме косинусов из треугольника ВСD найдем ВD. Ads by optAd360 BD2 = BC2 + CD2 – 2BC ∙ CD ∙ cos C = 82 + 152 – 2 ∙ 8 ∙ 15 ∙ = 64 + 225 – 120 = 169; 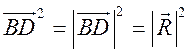 = 169; = 13. = 169; = 13.Ответ: 13. 2. Решить задачи № 1044 (а, б). 3. Устно № 1045. 4. Решить задачи № 1046, 1047 (б, в) на доске и в тетрадях. 5. Решить задачу № 1051. Решение 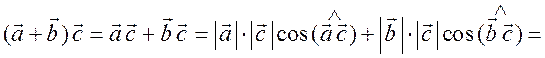 1 ∙ 2 cos 60° + 2 ∙ 2 cos 60° = 2 ∙ + 4 ∙ = 1 + 2 = 3. 1 ∙ 2 cos 60° + 2 ∙ 2 cos 60° = 2 ∙ + 4 ∙ = 1 + 2 = 3.Ответ: 3. 6. Решить задачу № 1049 на доске и в тетрадях (для угла А объясняет учитель): Решение 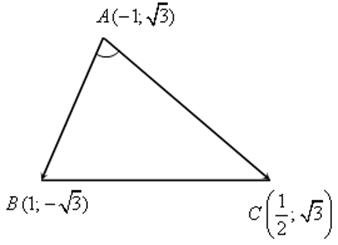 Ads by optAd360 1) cos A = 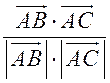 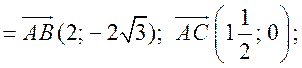 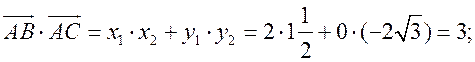 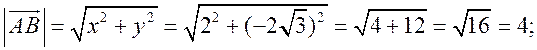 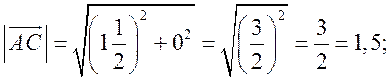 cos A = 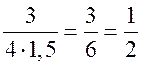 ; cos A = , то A = 60°. ; cos A = , то A = 60°.2) cos B = 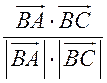 ; ; 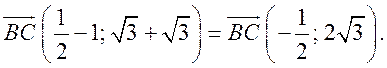 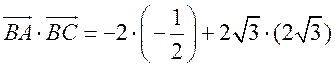 = 1 + 12 = 13; = 1 + 12 = 13;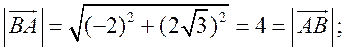 Ads by optAd360 BC = 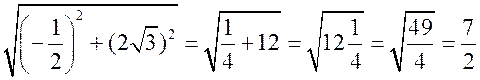 = 3,5; = 3,5;cos B = 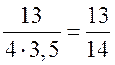 ≈ 0,9286; B находим по таблицам Брадиса: B ≈ 21°47′. ≈ 0,9286; B находим по таблицам Брадиса: B ≈ 21°47′.3) C = 180° – 60° – 21°47′ ≈ 98°13′. Ответ: A = 60°; B ≈ 21°47′; C ≈ 98°13′. 7. Решить задачу № 1052. Решение 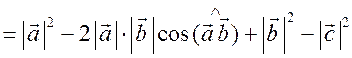 = 52 – 2 ∙ 5 ∙ 2 cos 90° + 22 – 42 = 25 + 4 – 16 = 13; = 13. = 52 – 2 ∙ 5 ∙ 2 cos 90° + 22 – 42 = 25 + 4 – 16 = 13; = 13.Ответ: 13. 8. Решить задачу № 1066. Решение По условию 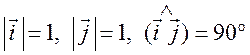 . .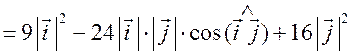 = 9 ∙ 1 – 24 ∙ 1∙ 1 ∙ 0 + 16 ∙ 1 = 25. = 9 ∙ 1 – 24 ∙ 1∙ 1 ∙ 0 + 16 ∙ 1 = 25.= 25, тогда = 5. Ads by optAd360 Ответ: 5. IV. Итоги урока. Домашнее задание: изучить материал пунктов 101–104; ответить на вопросы 17–20 на странице 271 учебника; решить №№ 1044 (в), 1047 (а), 1054 (разобрать решение задачи и записать в тетрадь). Решение задач - урок 4 - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА Цели: закрепление и проверка знаний и умений учащихся, сформированных при изучении главы XI, формирование навыков решения задач, развитие навыков логического мышления. Ход урока I. Математический диктант (10 мин). Вариант I 1. Вычислите скалярное произведение векторов и , если 2. Скалярное произведение ненулевых векторов и равно 0. Определите угол между векторами и . 3. Вычислите скалярное произведение векторов и , если (3; –2), (–2; 3). 4. Найдите угол между ненулевыми векторами (х; у) и (–у; х). 5. Вычислите косинус угла между векторами и , если (3; –4), (15; 8). 6. Даны векторы (2; –3) и (х; –4). При каком значении х эти векторы перпендикулярны? Вариант II 1. Вычислите скалярное произведение векторов и , если 2. Скалярное произведение ненулевых векторов и равно нулю. Определите угол между этими векторами. 3. Вычислите скалярное произведение векторов и , если (–4; 5), (–5; 4). 4. Найдите угол между ненулевыми векторами (х; –у) и (у; х). 5. Вычислите косинус угла между векторами и , если (–12; 5), (3; 4). 6. Даны векторы (3; у) и (2; –6). При каком значении у эти векторы перпендикулярны? II. Решение задач. 1. Решить задачу № 1025 (б, е, з) на доске и в тетрадях, используя микрокалькулятор. 2. Решить задачу № 1056 на доске и в тетрадях. Решение Пусть АВСD – данный ромб. Выразим векторы и через векторы и : Ads by optAd360 используя эти выражения, получаем: 3. Решить задачу № 1042 на доске и в тетрадях. 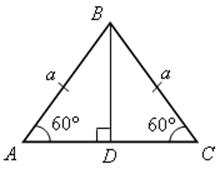 Решение АВ = ВС = АС = а; ВD АС. а) б) 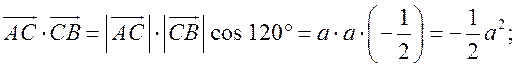 cos 120° = cos (180° – 60°) = –cos 60° = –. cos 120° = cos (180° – 60°) = –cos 60° = –.в) г) ответ: а) a2; б) –a2; в) 0; г) а2. Ads by optAd360 4. Решить задачу № 1050. Решение Скалярный квадрат вектора равен квадрату его длины, тогд. 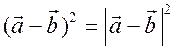 . . 52 – 2 ∙ 5 ∙ 8 ∙ + 82 = 25 – 40 + 64 = 49, 52 – 2 ∙ 5 ∙ 8 ∙ + 82 = 25 – 40 + 64 = 49, 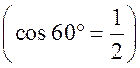 ; значит, = 7. ; значит, = 7.Самостоятельно учащиеся находят . III. Устный опрос учащихся по карточкам. Вариант I тангенс не существует и почему?? Для какого значения 1. Что называется тангенсом угла 2. Сформулируйте и докажите теорему синусов. 3. Даны векторы (х; –4) и (2; 3). Найдите значение х, если . Вариант II 1. Напишите формулы приведения. 2. Сформулируйте и докажите теорему косинусов. 3. Найдите скалярное произведение векторов (–5; 7) и (2; 1). Вариант III Ads by optAd360 1. Что такое скалярное произведение векторов? 2. Сформулируйте и докажите теорему о вычислении площади треугольника по двум сторонам и углу между ними. 3. Найдите косинус угла А треугольника АВС, если АВ = 8 см, АС = 6 см, ВС = 12 см. Вариант IV 1. Какие два вектора называются перпендикулярными? 2. Выведите формулу, выражающую косинус угла между ненулевыми векторами через их координаты. 3. Найдите синус угла В треугольника АВС, если АВ = 5 см, АС = 8 см, С = 30°. IV. Итоги уроков. Домашнее задание: подготовиться к контрольной работе, повторить материал пунктов 93–104; решить задачи №№ 1065, 1068, 1060 (а, б), 1061 (а, б). |
