геометрия. геометрия 9 класс. Ход уроков I. Повторение ранее изученного материала
 Скачать 0.76 Mb. Скачать 0.76 Mb.
|
|
Средняя линия трапеции - ПОНЯТИЕ ВЕКТОРА. РАВЕНСТВО ВЕКТОРОВ (10 урок) Цели: ввести понятия средней линии трапеции; доказать теорему о средней линии трапеции с помощью векторов; упражнять учащихся в решении задач. Ход урока I. Проверка усвоения учащимися материала. 1. Устно ответить на вопросы: 1) Какие векторы называются коллинеарными? Изобразите на рисунке сонаправленные векторы и и противоположно направленные векторы и . 2) Какой вектор называется произведением данного вектора на данное число? 3) Могут ли векторы и быть неколлинеарными? 4) Сформулируйте основные свойства умножения вектора на число. 2. Решить задачу на доске и в тетрадях по готовому чертежу: 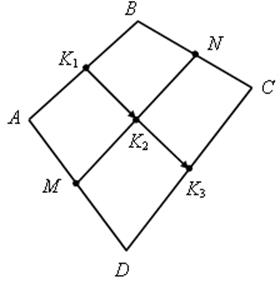 Точки M и N лежат соответственно на сторонах AD и BC четырехугольника ABCD, причем AM : MD = BN : NC = 3 : 4. Докажите, что середины отрезков AB, MN и CD лежат на одной прямой. Решение Пусть K1 – середина AB, K2 – середина MN, K3 – середина CD. Согласно задаче 2 из п. 84 имеем 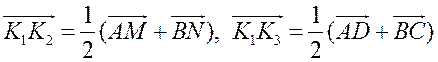 . Из условия следует, что . Из условия следует, что 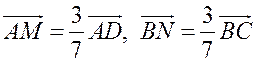 , поэтому , поэтому 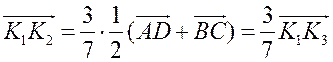 . .Таким образом, векторы и коллинеарные, и, значит, точки K1, K2 и K3 лежат на одной прямой. II. Объяснение нового материала. 1. Определение трапеции. Виды трапеций. 2. Определение средней линии трапеции. Ads by optAd360 3. Доказательство теоремы о средней линии трапеции (проводит сам учитель). При доказательстве теоремы целесообразно использовать результат задачи 2, решенной на предыдущем уроке. Доказательство можно оформить на доске и в тетрадях в виде следующей краткой записи: Дано: ABCD – трапеция, AD || BC, M – середина стороны AB; N – середина стороны CD (рис. 266 учебника). Доказать: MN || AD, MN = 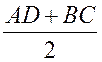 . .Доказательство 1) Согласно рассмотренной в классе задаче 1 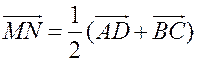 . .2) Так как 3) Так как III. Закрепление изученного материала (решение задач). 1. Решить на доске и в тетрадях задачу № 793. Решение Пусть a и b – основания трапеции, тогда а + b = 48 – (13 + 15) = 20 (см); средняя линия MN = 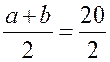 = 10 (см). = 10 (см).Ответ: 10 см. 2. Решить задачу № 795. Ads by optAd360 3. Решить задачу № 799 на доске и в тетрадях. 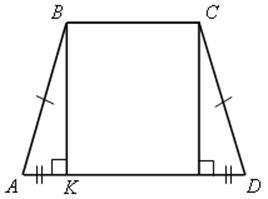 Решение Пусть BK – перпендикуляр, проведенный к основанию AD данной трапеции. Тогда KD = AD – AK. Но AK = 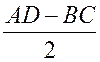 , поэтому KD = AD – , поэтому KD = AD –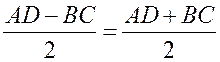 , то есть отрезок KD равен средней линии трапеции. Значит, средняя линия трапеции равна 7 см. , то есть отрезок KD равен средней линии трапеции. Значит, средняя линия трапеции равна 7 см.Ответ: 7 см. IV. Проверочная самостоятельная работа. Вариант I Точка K делит отрезок MN в отношении MK : KN = 3 : 2. Выразите вектор через векторы и , где A – произвольная точка. Вариант II Точка A делит отрезок EF в отношении EA : AF = 2 : 5. Выразите вектор через векторы и , где K – произвольная точка. Ads by optAd360 V. Итоги урока. Домашнее задание: изучить материал пункта 85; ответить на вопросы 18–20, с. 214 учебника; решить задачи №№ 787, 794, 796. Основные требования к учащимся: В результате изучения параграфа учащиеся должны знать, какой вектор называется произведением вектора на число; уметь формулировать свойства умножения вектора на число; знать, какой отрезок называется средней линией трапеции; уметь формулировать и доказывать теорему о средней линии трапеции; уметь решать задачи типа №№ 782–787; 793–799. Разложение вектора по двум данным неколлинеарным векторам - МЕТОД КООРДИНАТ (11 урок) Урок 1. Разложение вектора по двум данным неколлинеарным векторам Цели: доказать лемму о коллинеарных векторах и теорему о разложении вектора по двум неколлинеарным векторам и закрепить их знание в ходе решения задач. Ход урока I. Анализ результатов самостоятельной работы. II. Устная работа. 1. Устно решить задачи по заранее заготовленному чертежу на доске. Дан параллелограмм ABCD с диагоналями AC и BD, пересекающимися в точке О, а также отрезки MP и NQ, соединяющие соответственно середины сторон AB и CD, BC и AD. Требуется выразить. 1) вектор через вектор ; 2) вектор через вектор ; 3) вектор через вектор ; 4) вектор через вектор . 2. Вопрос учащимся. можно ли для любой пары коллинеарных векторов подобрать такое число, что один из векторов будет равен произведению второго вектора на это число? III. Изучение нового материала. 1. Формулировка леммы о коллинеарных векторах. Для понимания учащимися формулировки леммы полезно обсудить, во-первых, почему важно условие и, во-вторых, будет ли верно утверждение, если рассматривать произвольные (в том числе и неколлинеарные) ненулевые векторы. 2. Доказательство леммы. 3. Решить задачу по рисунку параллелограмма ABCD на доске (тем самым подвести учащихся к мысли о возможности выражения вектора через два данных неколлинеарных вектора): Точки M и Q – середины сторон AB и AD параллелограмма ABCD. Выразите: 1) вектор через векторы и ; 2) вектор через векторы и ; 3) вектор через векторы и ; Ads by optAd360 4) вектор через векторы и . 4. Рассмотреть теорему о разложении вектора по двум данным неколлинеарным векторам, в ходе ее доказательства полезно обратить внимание на роль леммы в доказательстве. IV. Закрепление изученного материала (решение задач). 1. Решить задачи № 911 (а, б); № 912 (б, в). 2. Решить задачи № 915 (по готовому чертежу) и № 916 (а, б). V. Итоги урока. Задание на дом: изучить материал пункта 86; решить задачи №№ 911 (в, г), 912 (ж, е, з), 916 (в, г). Координаты вектора - МЕТОД КООРДИНАТ (12 урок) Цели: ввести понятие координат вектора и рассмотреть правила действий над векторами с заданными координатами. Ход урока I. Проверка домашнего задания. 1. Устно решить задачи: 1) назвать числа х и у, удовлетворяющие равенству: 2) задача № 913. 2. На доске двое учащихся решают задачи №№ 911 (в) и 912 (и, к). II. Изучение нового материала. 1. Напомнить задание прямоугольной системы координат и начертить ее. 2. Ввести координатные векторы и (рис. 275). 3. Нулевой вектор можно представить в виде ; его координаты равны нулю: (0; 0). 4. Координаты равных векторов соответственно равны. 5. Рассмотреть правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число (доказательства указанных правил учащиеся могут рассмотреть самостоятельно). 6. Записать в тетрадях правила: 1) 2) 3) III. Закрепление изученного материала (решение задач). 1. Решить задачу № 917 на доске и в тетрадях. 2. Устно по рисунку 276 решить задачу № 918. 3. Решить задачу № 919 (самостоятельно). 4. Решить задачу № 920 (а, в) на доске и в тетрадях. 5. Устно решить задачи № 922–925, используя правила, записанные в тетрадях. Ads by optAd360 6. Записать утверждение задачи № 927 без доказательства: 1) Если два вектора коллинеарные, то координаты одного вектора пропорциональны координатам другого: если 2) Если координаты одного вектора пропорциональны координатам другого вектора, то эти векторы коллинеарные. 7. Решить задачу № 928. Решение Используем условие коллинеарности векторов: 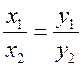 . .1) (3; 7) и (6; 14), так как ; 2) (–2; 1) и (2; –1), так как . IV. Самостоятельная работа контролирующего характера. Вариант I Решить задачи № 912 (а, г); № 920 (г); № 988 (а, б); № 921 (а, в); № 914 (а). Вариант II Решить задачи №№ 912 (в, д); 920 (д); 988 (в, г); 921 (б, г); 914 (б). V. Итоги урока. Домашнее здание: подготовиться к устному опросу по карточкам, повторить материал пунктов 76–87; ответить на вопросы 1–20, с. 213–214 и на вопросы 1–8, с. 249 учебника; решить задачи №№ 798, 795; 990 (а) (для векторов и ). Связь между координатами вектора и координатами его начала и конца. Простейшие задачи в координатах - МЕТОД КООРДИНАТ Цели: рассмотреть связь между координатами вектора и координатами его начала и конца; разобрать задачи о нахождении координат середины отрезка, о вычислении длины вектора по его координатам и нахождении расстояния между двумя точками. Ход урока I. Анализ результатов контрольной работы. 1. Указать ошибки, сделанные учащимися при выполнении работы. 2. Решить на доске задачи, вызвавшие затруднения у учащихся. II. Изучение нового материала (лекция). 1. Рассмотреть по учебнику рис. 277 и рис. 278 и ввести понятие радиус-вектора . Без доказательства записать в тетрадях утверждения: а) координаты точки М равны соответствующим координатам ее радиус-вектора; б) каждая координата вектора равна разности соответствующих координат его конца и начала: џ Устно решить задачу № 934. 2. Введение системы координат дает возможность изучать геометрические фигуры и их свойства с помощью уравнений и неравенств и, таким образом, использовать в геометрии методы алгебры. Такой подход к изучению свойств геометрических фигур называется методом координат. 3. Рассмотрим три вспомогательные задачи. 1) Координаты середины отрезка. Используя формулу из п. 84 (1) 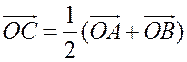 и координаты векторов и координаты векторов 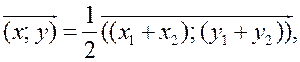 отсюда x = ; y = . отсюда x = ; y = .Вывод: каждая координата середины отрезка равна полусумме соответствующих координат его концов. џ Устно решить задачу № 936. 2) Вычисление длины вектора по его координатам. Ads by optAd360 Используя рис. 280 учебника, вывести формулу џ Устно решить задачу № 938. 3) Расстояние между двумя точками. Пусть точка M1 (x1; y1) и точка M2 (x2; y2); тогда вектор (x2 – x1; y2 – y1); следовательно, длина этого вектора может быть найдена по формуле 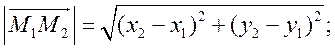 но но џ Решить задачу № 940 (а, б) на доске и в тетрадях. III. Закрепление изученного материала (решение задач). 1. Решить задачу № 939. Решение Найти расстояние от точки М (3; –2): а) до оси абсцисс; точка В (x; y) лежит на оси абсцисс; тогда расстояние равно 2; б) расстояние до оси ординат равно 3; в) до начала координат равно d = 2. Решить задачу № 941 на доске и в тетрадях. Решение PΔ = MN + NP + MP; MN = NP = Ads by optAd360 MP = PΔMNP = IV. Итоги урока. Задание на дом: изучить материал пунктов 88, 89; решить задачи №№ 935, 952. Простейшие задачи в координатах. Решение задач - МЕТОД КООРДИНАТ Цели: закрепить знания учащихся в ходе решения задач; учить решать задачи в координатах. Ход урока I. Повторение изученного материала. 1. Двое учащихся по карточкам работают у доски: Карточка 1 1) Вывести формулы координат середины отрезка. 2) Решить задачу № 942. Карточка 2 1) Вывести формулу расстояния между двумя точками. 2) Решить задачу № 937. 2. С остальными учащимися проводится устная работа по решению задач: 1) Найдите координаты вектора , равного разности векторов и , если (–5; 6), (0; –4). 2) Найдите координаты вектора , равного сумме векторов и , если (3; 7), (4; –5). 3) Найдите координаты середины отрезка DK, если D (–6; 4), K (2; –8). 4) Найдите длину отрезка CP, если С (3; –2), P (–5; 4). 5) Найдите длину вектора , равного , если (5; 0) и (0; –12). 6) Найдите координаты вектора 3, если (4; –2); вектора –2, если (–2; 5). II. Решение задач. 1. Решить задачу № 947 (а). Решение  Ads by optAd360 Найдем длины сторон треугольника АВС по формуле d = AB = BC = AC = Так как АВ = АС, то по определению равнобедренного треугольника АВС – равнобедренный. Найдем его площадь; проведем высоту АМ ВС: SΔABC = BC ∙ AM; AM – высота и медиана в равнобедренном треугольнике. Пусть М (x; y), тогда x = 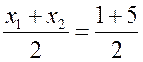 = 3; y = = –1. Значит, точка М (3; –1). Найдем длину отрезка AM = = 3; y = = –1. Значит, точка М (3; –1). Найдем длину отрезка AM = Площадь треугольника АВС равна S = 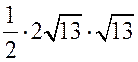 = 13. = 13.Ответ: 13. 2. Решить задачу № 946 (б). Решение M1 (–1; x) и M2 (2x; 3); M1M2 = d = 7. Найти x. d = 4x2 + 4x + 1 + 9 – 6x + x2 = 49; 5x2 – 2x – 39 = 0; Ads by optAd360 D = b2 – 4ac = 4 + 780 = 784; 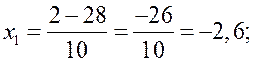 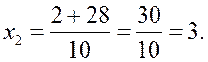 Ответ: –2,6; 3. 3. Решить задачу № 948 (б) на доске и в тетрадях. Решение Пусть точка М (0; y) лежит на оси ординат; по условию МС = MD; (4 – 0)2 + (–3 – y)2 = (8 – 0)2 + (1 – y)2; 16 + 9 + 6y + y2 = 64 + 1 – 2y + y2; 8y = 40; y = 5. Значит, точка М (0; 5). Ответ: (0; 5). 4. Решить задачу № 950 (б) на доске и в тетрадях. Решение 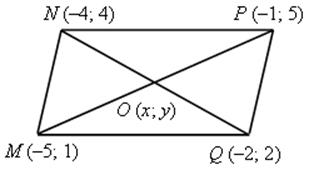 Найдем координаты точки пересечения диагоналей четырехугольника О (x; y): для диагонали NQ имеем: x = 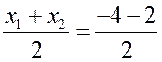 = –3; y = = 3; точка О (–3; 3). = –3; y = = 3; точка О (–3; 3).Ads by optAd360 Для диагонали МР имеем: x = = –3; y = 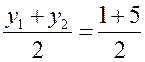 = 3; точка О (–3; 3). = 3; точка О (–3; 3).Значит, диагонали MP и NQ точкой пересечения делятся пополам; по признаку параллелограмма MNPQ – параллелограмм. MP = NQ = Ответ: 4 и 2 . 5. Решить задачу № 951 (а). Решение AB = CD = BC = AD = Так как AB = CD = 4 и BC = AD = 2, то по II признаку параллелограмма ABCD – параллелограмм. Найдем диагонали АС и BD параллелограмма ABCD: AC = BD = Если диагонали равны AC = BD, то ABCD – прямоугольник. S = AD ∙ AB = 2 ∙ 4 = 8. Ads by optAd360 Ответ: 8. III. Итоги урока. Домашнее здание: повторить материал пунктов 88 и 89; решить задачи №№ 947 (б), 949 (а), 951 (б), 953. |
