Методические указания к Типовому расчету. Методические указания к Типовому расчету ВАЖНАЯ ХУЙНЯ. ижевский государственный технический университет

• Название: ижевский государственный технический университет
• Анкор: Методические указания к Типовому расчету
• Дата: 21.05.2021
• Размер: 1.52 Mb.
• Имя файла: Методические указания к Типовому расчету ВАЖНАЯ ХУЙНЯ.doc
• Тип: Методические указания; #208184
• страница: 5 из 14

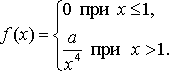Найдите: 1) функцию распределения F(x)и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал (0: 5) . Постройте графики функций распределения и плотности распределения

Вариант 3

1. 
   А). Сколько перестановок можно получить из букв слова АЛЬБОМ?
   Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?
   

2. 
   А). Сколько перестановок можно получить из цифр числа 345642353 ?
   Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?
   

3. 
   Из букв слова ПРОСТЫНЯ составляются пятибуквенные слова.
   А).Сколько таких слов можно получить?
   Б) Сколько таких слов начинается с буквы П?
   В) А если слова содержат не менее 5 букв?
   

4. 
   Решить уравнение
   
5. 
   
   

   На рисунке приведены схемы электрических цепей. События: ={элемент k работает}; С={ в цепи нет разрыва}. Выразить события и через события и .

6. 
   В букете, состоящем из 9 цветов 4 красных цветка, остальные синие. Наудачу берется 5 цветов. Определить вероятность того, что красных цветов среди них будет а) ровно 2 штуки; б) не более двух.
   
7. 
   Точка (c, q) наудачу выбирается из квадрата с вершинами (0,0), (1,0), (1,1), (0,1). Найдите вероятность того, что корни уравнения х² +сх + q = 0 окажутся действительными и одного знака.
   
8. 
   В первой урне содержится 10 шаров, из них 8 белых; во второй урне 20 шаров, из них 4 белых. Из каждой урны наудачу извлекли по одному шару, а затем из этих шаров наудачу взят один шар. а)Найдите вероятность того, что взят белый шар.б) Выбранный шар оказался белым. Какова вероятность, что он взят из первой урны?
   
9. 
   Наблюдениями установлено, что в некоторой местности в июле в среднем бывает 12 дождливых дней. Какова вероятность того, что из восьми случайно выбранных в этом месяце дней а ) ровно три окажутся дождливыми; б) дождливыми окажутся хотя бы два дня; в) дождливыми будут не более 7 дней?
   
10. 
    Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течение времени t равна 0,002. Найдите вероятность того, что за время t откажут ровно 3 элемента.
    

11. 
    Вероятность того, что станок-автомат произведет годную деталь, равна 9/11. за смену было изготовлено 330 деталей. Определить вероятность того, что среди них а) 40 бракованных; б) бракованных деталей не более 40, но не менее 2.
    

12. 
    Дан ряд распределения случайной величины Х.
    а)Найти значение *;
    б) изобразить полигон распределения;
    в) найти и изобразить графически функцию распределения;
    г )найти вероятность того, что случайная величина Х примет значение в интервале
    [3,5; 7,5);
    д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5);
    е) найти математическое ожидание случайной величины Х;
    ж) найти дисперсию случайной величины Х;
    
    
    

xi	1	2	5	7
pi	0,3	0,2	0,1	*

13. 
    Даны законы распределения двух случайных величин Х и Y:
    Найти закон распределения случайных величин а )Z=3X+Y; б)U=XY.
    
    
    

xi	0	1	2	4
pi	0,1	0,1	0,3	0,5

yi	-2	0	2	4
pi	0,1	0,2	0,1	0,6

14. 
    Случайная величина Х задана функцией плотности распределения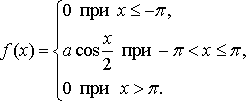
    

Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал . Постройте графики функций распределения и плотности распределения .

Вариант 4

1. 
   Сколько перестановок можно получить из букв слова ТЕСАК ?
   Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?
   

2. 
   А). Сколько перестановок можно получить из цифр числа 768987864?
   Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?
   

3. 
   И з букв слова ПРОЕКЦИЯ составляются пятибуквенные слова.
   А).Сколько таких слов можно получить?
   Б) Сколько таких слов начинается с буквы П?
   В) А если слова содержат не менее 5 букв?
   
4. 
   Решить уравнение
   

На рисунке приведена схема электрической цепи. События: ={элемент k работает}; С={ в цепи нет разрыва}. Выразить события и через события и .

6. 
   В студенческой группе 15 человек, из которых 5 девушек, а остальные – юноши. Деканат дал студентам этой группы 5 билетов на концерт группы «Тылобурдо». Найти вероятность, что а)3 билета достанутся девушкам; б) не менее трех билетов достанутся девушкам.
   
7. 
   Из отрезка [0, 2] на удачу выбраны два числа х и у. Найдите вероятность того, что эти числа удовлетворяют неравенствам х² £ 4у £ 4х.
   

8. 
   70% учащихся в Ижгту — юноши. 80% девушек и 60% юношей имеют билеты на КВН. В деканат принесли кем-то потерянный билет. Какова вероятность того, что этот билет при­надлежал девушке? Юноше?
   
9. 
   Рабочий обслуживает 12 однотипных станков. Вероятность, что станок потребует внимания рабочего в течение промежутка времени Т, равна 1/3. Найти вероятность того, что за время Т а) 4 станка потребуют внимания рабочего; б) менее 4-х станков .потребуют внимания рабочего; в) хотя бы 4 станка потребуют внимания рабочего.
   

10. 
    Вероятность нарушения герметичности банки в некоторой партии консервных банок равна 0,0004. Вычислите вероятность того, что среди 2000 банок окажутся с нарушением герметичности не более 3.
    
11. 
    Вероятность того, что деталь не прошла проверку ОТК равна р = 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных а) ровно 60; б) от 70 до 100.
    

12. 
    Дан ряд распределения случайной величины Х.
    а)Найти значение *;
    б) изобразить полигон распределения;
    в) найти и изобразить графически функцию распределения;
    г )найти вероятность того, что случайная величина Х примет значение в интервале
    [3,5; 7,5);
    д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5);
    е) найти математическое ожидание случайной величины Х;
    ж) найти дисперсию случайной величины Х;
    
    
    

xi	-1	3	4	5
pi	*	0,2	0,1	0,3

13. 
    Даны законы распределения двух случайных величин Х и Y:
    Найти закон распределения случайных величин а )Z=X+3Y; б)U=XY.
    
    
    

xi	-4	0	1	2
pi	0,2	0,1	0,2	0,5

yi	-1	0	2	4
pi	0,2	0,2	0,5	0,1

14. 
    Случайная величина Х задана функцией плотности распределения
    

Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал . Постройте графики функций распределения и плотности распределения .

Вариант 5

1. 
   А). Сколько перестановок можно получить из букв слова САМОЛЕТ ?
   Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?
   

2. 
   А). Сколько перестановок можно получить из цифр числа 465768756?
   Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?
   

3. 
   Из букв слова ПРОГУЛКА составляются пятибуквенные слова.
   А).Сколько таких слов можно получить?
   Б) Сколько таких слов начинается с буквы П?
   В) А если слова содержат не менее 5 букв?
   

4. 
   Решить уравнение
   

На рисунке приведена схема электрической цепи. События: ={элемент k работает}; С={ в цепи нет разрыва}. Выразить события и через события и .

6. 
   У Малыша в кульке лежали 12 конфет: 5 карамелек и 7 шоколадных. Карлсон не глядя запустил в кулек руку и достал 8 конфет. Найти вероятность того, что у Карлсона в руке оказалось а) 6 шоколадных конфет и 2 карамельки; б) карамелек оказалось не более 2.
   
7. 
   Найдите вероятность того, что сумма двух наудачу взятых чисел из отрезка [-1,1] больше нуля, а их произведение отрицательно
   
8. 
   Бросается монета, и если она падает так, что сверху ока­зывается герб, вынимаем один шар из урны I; в противном случае — из урны II. Урна I содержит 4 красных и 1 белый шар. Урна II содержит 1 красный и 3 белых шара, а) Какова вероятность того, что вынутый шар красный? б) Какова вероятность того, что шар вынимался из I урны, если он оказался красным?
   
9. 
   Китайский завод изготавливает изделия, каждое из которых с вероятностью 1/3 оказывается дефектным. Для контроля продукции выбирается 6 изделий. Найти вероятность того, что а) ни в одном изделии не будет дефекта; б) не менее чем в двух изделий будет обнаружен дефект; в) ровно в трех изделиях будет дефект.
   
10. 
    Вероятность появления брака при автоматической обработке деталей равна 0,003. Найдите вероятность того, что среди 1000 деталей только 4 детали будут бракованными.
    

11. 
    Вероятность выхода конденсатора из строя в течение времени t равна 0,25. Вычислите вероятность того, что за этот промежуток времени из имеющихся 150 конденсаторов выйдет из строя а) ровно 60 конденсаторов; б) от 40 до 80 конденсаторов.
    

12. 
    Дан ряд распределения случайной величины Х.
    а)Найти значение *;
    б) изобразить полигон распределения;
    в) найти и изобразить графически функцию распределения;
    г )найти вероятность того, что случайная величина Х примет значение в интервале
    [3,5; 7,5);
    д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5);
    е) найти математическое ожидание случайной величины Х;
    ж) найти дисперсию случайной величины Х;
    
    
    

xi	0	3	6	7
pi	0,1	0,3	0,1	*

13. 
    Даны законы распределения двух случайных величин Х и Y:
    Найти закон распределения случайных величин а )Z=X-2Y; б)U=XY.
    
    
    

xi	-1	0	1	2
pi	0,4	0,1	0,3	0,2

yi	-2	0	1	2
pi	0,1	0,3	0,1	0,5

14. 
    Случайная величина Х задана функцией плотности распределения