Методические указания к Типовому расчету. Методические указания к Типовому расчету ВАЖНАЯ ХУЙНЯ. ижевский государственный технический университет
 Скачать 1.52 Mb.
|
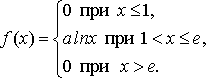 Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал . Постройте графики функций распределения и плотности распределения . Вариант 9 А). Сколько перестановок можно получить из букв слова КУЛЕБЯКА? Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов? А). Сколько перестановок можно получить из цифр числа 475638575 ? Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов? Из букв слова ПРИМЕР составляются пятибуквенные слова. А).Сколько таких слов можно получить? Б) Сколько таких слов начинается с буквы П? В) А если слова содержат не менее 5 букв? Решить уравнение 
В конкурсе мисс ИжГТУ участвовало 13 девушек. Среди них было 6 блондинок и 7 брюнеток. Первокурсник ИВТ факультета пригласил в кино их всех, но пришли только 5 девушек. Найти вероятность того, что первокурсник смотрел кино а) 5 блондинками ; б) двумя блондинками и тремя брюнетками. Точка (c, q) наудачу выбирается из квадрата с вершинами (0,0), (1,0), (1,1), (0,1). Найдите вероятность того, что корни уравнения х2 +сх + q = 0 окажутся действительными положительными числами? В каждой из 3 урн по 6 черных и 4 белых шара. Из первой урны наудачу извлечен один шар и переложен во вторую, после чего из второй урны наудачу извлечен один шар и переложен в третью урну. Найдите вероятность того, что шар, извлеченный затем из третьей урны, окажется белым. Игральная кость подбрасывается 9 раз. Найти вероятность того, что а) шестерка выпадет 3 раза; б) шестерка выпадет более трех раз; в) шестерка выпадет не более семи раз. Устройство состоит из 1600 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течение времени t равна 0,001. Найдите вероятность того, что за время t 4 элемента. Вероятность изготовления детали со стандартными размерами равна 0,7. Вычислите вероятность того, что среди 300 деталей стандартными будут от 200 до 250. Дан ряд распределения случайной величины Х. а)Найти значение *; б) изобразить полигон распределения; в) найти и изобразить графически функцию распределения; г )найти вероятность того, что случайная величина Х примет значение в интервале [3,5; 7,5); д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5); е) найти математическое ожидание случайной величины Х; ж) найти дисперсию случайной величины Х;
Даны законы распределения двух случайных величин Х и Y: Найти закон распределения случайных величин а )Z=X+3Y; б)U=XY.
Случайная величина Х задана функцией плотности распределения 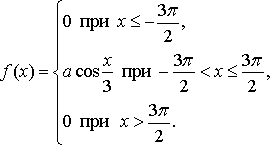 Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал  . Постройте графики функций распределения и плотности распределения .Вариант 10 А). Сколько перестановок можно получить из букв слова БОЧКА? Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов? А). Сколько перестановок можно получить из цифр числа 274655733 ? Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов? Из букв слова ПРИВОЛЬЕ составляются пятибуквенные слова. А).Сколько таких слов можно получить? Б) Сколько таких слов начинается с буквы П? В) А если слова содержат не менее 5 букв? Р  ешить уравнение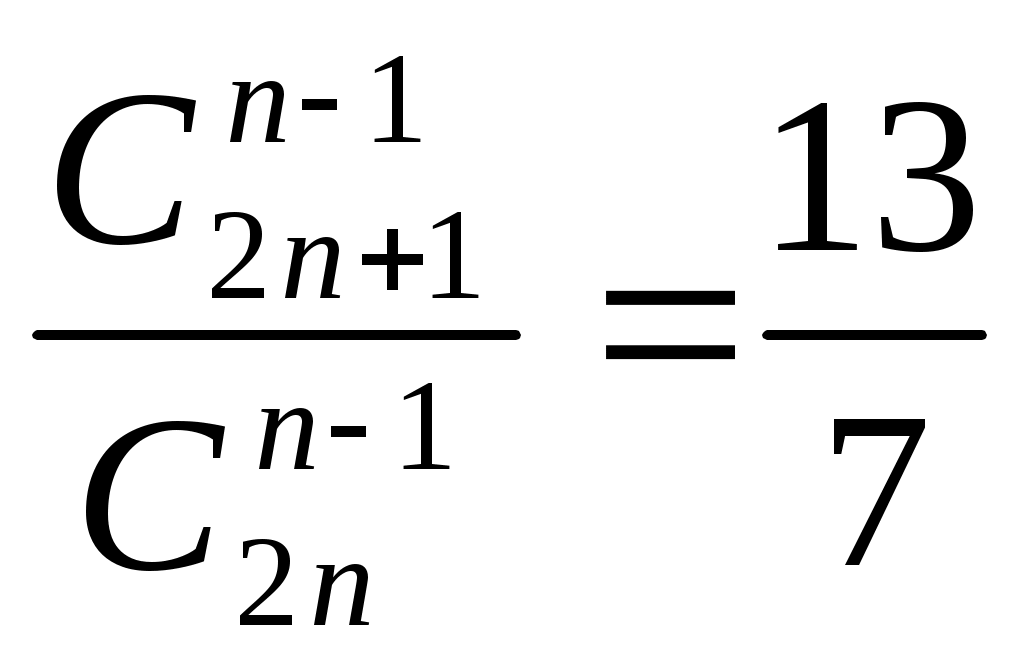 
У одной одинокой бабушки было 12 кошек. Среди которых были 5 короткошерстных и 7 длинношерстных. На 8 марта одинокая бабушка решила подарить 5 кошечек соседям. Выбирала она их случайным образом. Найти вероятность того, что среди подарочков а) ровно 4 кошки были длинношерстные; б) длинношерстных кошек было не менее четырех. Какова вероятность того, что сумма двух наугад взятых положительных чисел, каждое из которых не больше трех, не превзойдет трех, а их произведение будет не больше 2/7? С первого станка-автомата на сборку поступают 40%, со второго — 30%, с третьего — 20%, с четвертого — 10% деталей. Среди деталей, выпущенных первым станком, 2% бракованных, вторым — 1 %, третьим — 0,5% и четвертым — 0,2%. а)Найдите вероятность того, что поступившая на сборку деталь небракованная. Известно, что поступившая на сборку деталь небракованная. Какова вероятность, что она выпущена третьим станком? Монету подбрасывают 10 раз. Какова вероятность того, что герб выпадет: а) три раза; б) не менее трех раз; в) более 7 раз. Какова вероятность того, что среди 200 человек будет 6 левшей, если левши в среднем составляют 1%? Вероятность, что рост человека находится в интервале от 164 до 174 равна 0,8. а) Найдите вероятность того, что среди встретившихся вам на улице 300 человек рост ровно 125 человек не будет находиться в интервале от 164 до 174.б) Найдите вероятность того, что среди встретившихся вам на улице 300 человек будут от 120 до 250 человек, чей рост находиться в интервале от 164 до 174. Дан ряд распределения случайной величины Х. а)Найти значение *; б) изобразить полигон распределения; в) найти и изобразить графически функцию распределения; г )найти вероятность того, что случайная величина Х примет значение в интервале [3,5; 7,5); д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5); е) найти математическое ожидание случайной величины Х; ж) найти дисперсию случайной величины Х;
Даны законы распределения двух случайных величин Х и Y: Найти закон распределения случайных величин а )Z=2X+Y; б)U=XY
Случайная величина Х задана функцией плотности распределения  Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал  . Постройте графики функций распределения и плотности распределения .Вариант 11 А). Сколько перестановок можно получить из букв слова ДОСУГ ? Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов? А). Сколько перестановок можно получить из цифр числа 586758475? Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов? Из букв слова ПРИКЛАД составляются пятибуквенные слова. А).Сколько таких слов можно получить? Б) Сколько таких слов начинается с буквы П? В) А если слова содержат не менее 5 букв? Решить уравнение 
В ящике содержится 10 деталей, среди которых 4 нестандартные. Определить вероятность того, что в наудачу отобранных 6 деталях окажется а) ровно две нестандартные; б) не более двух нестандартных. На отрезке длиной а наудачу ставится 2 точки, в результате чего отрезок оказывается разделенным на три части. Определить вероятность того, что из трех получившихся частей отрезка можно построить треугольник. Из 5 стрелков 2 попадают в цель с вероятностью 0,6 и 3 — с вероятностью 0,4. а) Что вероятнее: попадет в цель наудачу выбранный стрелок или нет? б) Наудачу выбранный стрелок попал в цель. Что вероятнее: принадлежит он к первым двум или к трем последним? Транзисторный радиоприемник смонтирован на 10 полупроводниках, для которых вероятность брака равна 1/4. приемник отказывает при наличии не менее трех бракованных полупроводников. Найти вероятность того, что: а) откажут ровно 4 полупроводника; б) приемник будет работать; в) приемник откажет. Устройство состоит из 1500 элементов, работающих независимо один от другого. Вероятность отказа каждого из них в течение времени t равна 0,0017. Найдите вероятность того, что за время t откажут от 2 до 4 элементов. Из большой партии продукции, содержащей 70% изделий первого сорта, наугад отбирают 100 изделий. Вычислите вероятность того, что среди отобранных будет а) ровно 80 изделий 1 сорта; б) не менее 50 и не более 90 изделий первого сорта. Дан ряд распределения случайной величины Х. а)Найти значение *; б) изобразить полигон распределения; в) найти и изобразить графически функцию распределения; г )найти вероятность того, что случайная величина Х примет значение в интервале [3,5; 7,5); д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5); е) найти математическое ожидание случайной величины Х; ж) найти дисперсию случайной величины Х;
Даны законы распределения двух случайных величин Х и Y: Найти закон распределения случайных величин а )Z=X-4Y; б)U=XY
Случайная величина Х задана функцией плотности распределения |
={элемент k работает}; С={ в цепи нет разрыва}. Выразить события 
и 
через события 
.
через события 
