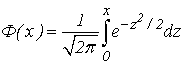Методические указания к Типовому расчету. Методические указания к Типовому расчету ВАЖНАЯ ХУЙНЯ. ижевский государственный технический университет

• Название: ижевский государственный технический университет
• Анкор: Методические указания к Типовому расчету
• Дата: 21.05.2021
• Размер: 1.52 Mb.
• Имя файла: Методические указания к Типовому расчету ВАЖНАЯ ХУЙНЯ.doc
• Тип: Методические указания; #208184
• страница: 14 из 14

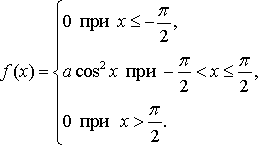Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал . Постройте графики функций распределения и плотности распределения .
Вариант 30

1. 
   А). Сколько перестановок можно получить из букв слова ЗЕНИТ?
   Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?
   
   
   
2. 
   А). Сколько перестановок можно получить из цифр числа 17364735627?
   Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?
   
   
   
3. 
   Из букв слова ПАРОДИЯ составляются пятибуквенные слова.
   А).Сколько таких слов можно получить?
   Б) Сколько таких слов начинается с буквы П?
   В) А если слова содержат не менее 5 букв?
   
   
   
4. 
   Решить уравнение
   

   	На рисунке приведена схема электрической цепи. События: ={элемент k работает}; С={ в цепи нет разрыва}. Выразить события и через события и .
   	У одной одинокой бабушки было 15 кошек. Среди которых были 8 короткошерстных и 7 длинношерстных. На 8 марта одинокая бабушка решила подарить 7 кошечек соседям. Выбирала она их случайным образом. Найти вероятность того, что среди подарочков а) ровно 4 кошки были длинношерстные; б) длинношерстных кошек было не менее четырех.

5. 
   Плоскость разграфлена параллельными прямыми, находящимися на расстоянии 3а друг от друга. На плоскость наудачу брошена монета радиуса г<a. найти вероятность того, что монета не пересечет ни одной из прямых.
   
6. 
   В сборной ИжГТУ по футболу 7 игроков с «ИВТ» факультета, 8 – с «ТТ», 6 – с
   «РиДа» и 4 – с МиМ факультета. Статистикой установлено, что вероятность забить гол в играх сборной для студента «ИВТ» факультета составляет 0,5, для студента «ТТ» факультета 0,4, для «РиДовца» 0,35 и для «МиМовца» 0,3. В матче футболистами забито 2 гола. Какова вероятность того, что один гол забил представитель «ИВТ» факультета, другой – представитель МиМ факультета?
   
7. 
   Монету подбрасывают 10 раз. Какова вероятность того, что герб выпадет: а) четыре раза; б) не менее четырех раз; в) не более 8 раз.
   
8. 
   По данным ОТК в среднем 3% изделий требуют дополнительной регулировки. Вычислите вероятность того, что из 200 изделий 4 потребуют дополнительной регулировки.
   

11. 
    В цехе имеется 90 станков, работающих независимо друг от друга. Для каждого станка вероятность быть включенным равна 0,9. Вычислите вероятность того, что в некоторый момент времени выключенными окажутся а) ровно 50 станков; б) от 60 до 75 станков.
    

12. 
    Дан ряд распределения случайной величины Х.
    а)Найти значение *;
    б) изобразить полигон распределения;
    в) найти и изобразить графически функцию распределения;
    г )найти вероятность того, что случайная величина Х примет значение в интервале
    [3,5; 7,5);
    д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5);
    е) найти математическое ожидание случайной величины Х;
    ж) найти дисперсию случайной величины Х;
    
    
    

xi	-2	1	3	4
pi	0,4	0,25	0,1	*

13. 
    Даны законы распределения двух случайных величин Х и Y:
    Найти закон распределения случайных величин а )Z=X+Y; б)U=XY.
    
    
    

xi	0	1	2	4
pi	0,1	0,1	0,3	0,5

yi	-2	0	2	4
pi	0,1	0,2	0,1	0,6

14. 
    Случайная величина Х задана функцией плотности распределения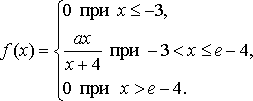
    

Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал . Постройте графики функций распределения и плотности распределения .


ПРИЛОЖЕНИЕ I

Таблица значений функции

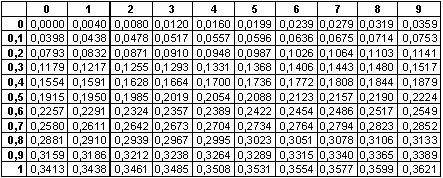
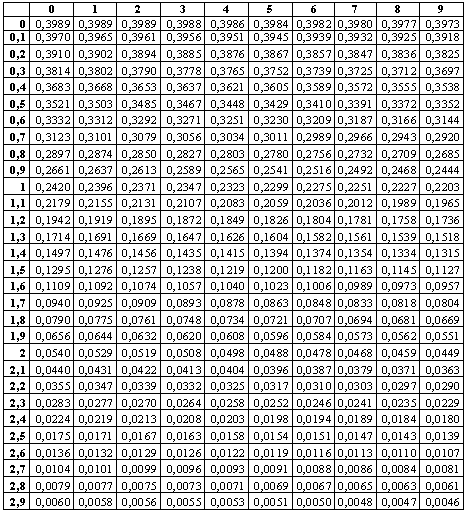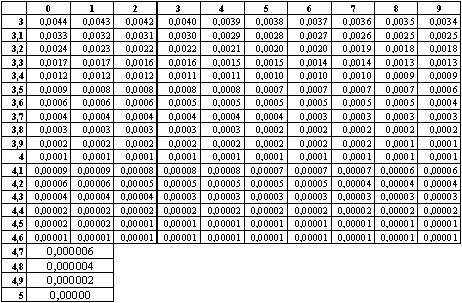ПРИЛОЖЕНИЕ II

Таблица значений функции Лапласа

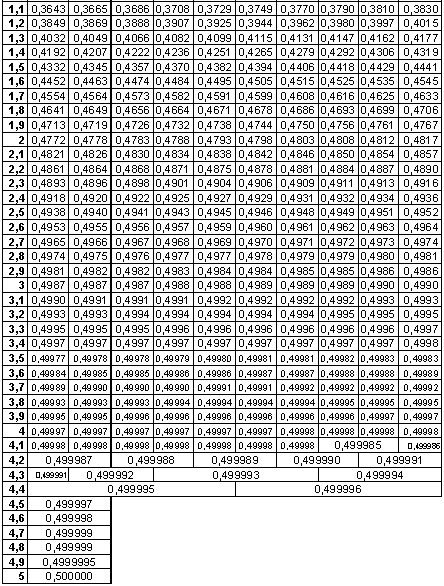ПРИЛОЖЕНИЕ III

Таблица значений функции Пуассона

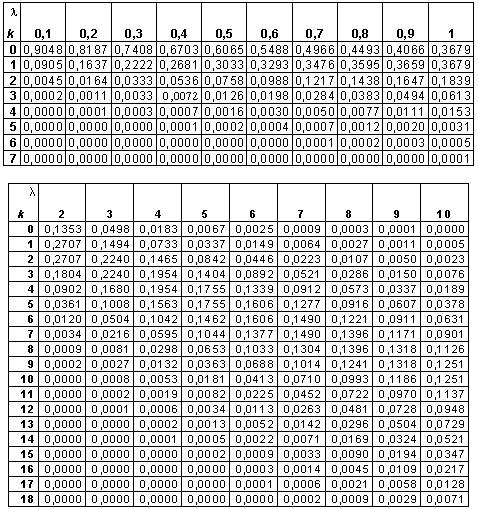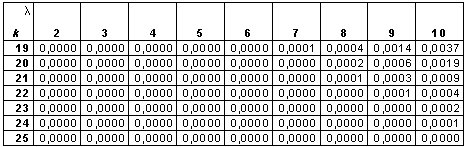Литература
Основная литература
1. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов вузов. Изд 4-е, стер. – М.: Высш. шк., 1998. – 400 с.

2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнения и задачах. В 2-х ч. Ч. II: Учеб. пособие для втузов. – 5-е изд., испр. – М.: Высш. шк., 1997. – 416 с.

3. Гмурман В.Е. Теории вероятностей и математическая статистика: Учеб. пособие для вузов. Изд 6-е, стер. – М.: Высш. шк., 1998. – 479 с.

4. Карасев А.И., Аксютина З.М., Савельева Т.И. Курс высшей математики для экономических вузов. В 2-х частях. Ч. II. Теория вероятностей и математическая статистика. Линейное программирование. –М.: Высшая школа, 1982.
Дополнительная литература
5. Бронштейн И.Н., Семендяев К. А. Справочник по математике для инженеров и учащихся ВТУЗов. - М.: Наука, 1986.

6. Вентцель Е.С. Теория вероятностей: Учеб. для вузов. – 5-е изд. стер. – М.: Высш. шк., 1998. – 576 с.

7. Колде Я.К. Практикум по теории вероятностей и математической статистике: Учебное пособие для техникумов. – М.: Высшая школа, 1991. – 157 с.