Методические указания к Типовому расчету. Методические указания к Типовому расчету ВАЖНАЯ ХУЙНЯ. ижевский государственный технический университет
 Скачать 1.52 Mb. Скачать 1.52 Mb.
|
 Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал . Постройте графики функций распределения и плотности распределения . Вариант 27 А). Сколько перестановок можно получить из букв слова МАЙОНЕЗ? Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов? А). Сколько перестановок можно получить из цифр числа 4857364585? Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов? Из букв слова ПЕЧНИК составляются пятибуквенные слова. А).Сколько таких слов можно получить? Б) Сколько таких слов начинается с буквы П? В) А если слова содержат не менее 5 букв? Решить уравнение
В лотерее «Спортлото 5 из 35» участник лотереи, правильно угадавший 4 или 5 видов спорта из 35 , получает денежный приз. Найти вероятность того, что данный участник угадает а) 5 видов спорта; б) получит денежный приз. Лиса Алиса и Кот Базилио договорились встретиться на Поле Чудес в Стране Дураков между 11 и 12 часами ночи. Каждый из них может прийти к месту встречи в любой промежуток времени от 10 до 11 часов ночи. Определить вероятность того, что время ожидания одним другого будет не больше 20 минут. На 3 дочерей — Алису, Марину и Елену — в семье возложена обязанность мыть посуду. Поскольку Алиса старшая, ей приходится выполнять 40% всей работы. Остальные 60% работы Марина и Елена делят поровну. Когда Алиса моет посуду, вероятность для нее разбить по крайней мере одну тарелку равна 0,02. Для Марины и Елены эта вероятность равна соответственно 0,03 и 0,04. Родители не знают, кто мыл посуду вечером, но они слышали звон разбитой тарелки. Какова вероятность того, что посуду мыла Елена? Среди коконов некоторой партии 40% цветных. Какова вероятность того, что среди 10 отобранных коконов а) цветных будет 3 кокона; б) цветных коконов будет не менее трех; в) цветных коконов будет не более 9. Вероятность попадания в цель при каждом выстреле равна 0,001. Найдите вероятность попадания в цель двумя и более выстрелами при залпе из 3000 орудий. Прядильщица обслуживает 1000 веретен. Вероятность обрыва нити на одном веретене в течение минуты равна 0,002. Найти вероятность того, что в течение минуты обрыв произойдет на а) трех веретенах; б) от 13 до 40 веретенах. Дан ряд распределения случайной величины Х. а)Найти значение *; б) изобразить полигон распределения; в) найти и изобразить графически функцию распределения; г )найти вероятность того, что случайная величина Х примет значение в интервале [3,5; 7,5); д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5); е) найти математическое ожидание случайной величины Х; ж) найти дисперсию случайной величины Х;
Даны законы распределения двух случайных величин Х и Y: Найти закон распределения случайных величин а )Z=X+Y; б)U=XY.
Случайная величина Х задана функцией плотности распределения 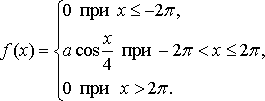 Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал Вариант 28 А). Сколько перестановок можно получить из букв слова КУПОЛ? Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов? А). Сколько перестановок можно получить из цифр числа 12343263429? Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов? Из букв слова ПЛАНШЕТ составляются пятибуквенные слова. А).Сколько таких слов можно получить? Б) Сколько таких слов начинается с буквы П? В) А если слова содержат не менее 5 букв? Решить уравнение
В аудитории находятся 25 студентов. 10 из них изучают английский язык, а остальные 15 – французский. Случайным образом для уборки территории отбираются 7 студентов. Найти вероятность того, что среди них а) ровно 3 изучают английский язык; б) студентов изучающих французский больше. Улитка переползает тропинку за 9 минут. Какова вероятность того, что улитка заметит ползущего по тропинке жука, если она может это сделать лишь в том случае, когда жук находится не более чем в трех минутах до пересечения курса улитки, или не более чем в трех минутах после пересечения жуком курса улитки. Курс жука перпендикулярен курсу улитки. Агентство по страхованию автомобилей разделяет водителей по 3 классам: класс Н1 (мало рискует), класс H2 (рискует средне), класс H3 (рискует сильно). Агентство предполагает, что из всех водителей, застраховавших автомобили, 30% принадлежат к классу 50% — к классу H2 и 20% — к классу H3. Вероятность того, что в течение года водитель класса Н1 попадет хотя бы в одну аварию, равна 0,01, для водителя класса H2 эта вероятность равна 0,02, а для водителя класса H3 — 0,08. Водитель А страхует свою машину и в течение года попадает в аварию. Какова вероятность того, что он относится к классу H3? По каналу связи передается 8 сообщений. Каждое из них независимо от других с вероятностью 0,1 искажается помехами. Найти вероятности следующих событий: а) из 8 событий ровно 5 искажаются помехами; б) искажаются помехами не более половины всех передаваемых сообщений; в) помехами искажается более 5 сообщений. При изготовлении радиоламп в среднем бывает 2% брака. Найдите вероятность того, что в партии из 200 ламп не более двух бракованных. Коммутатор учреждения обслуживает в среднем 100 абонентов. Вероятность того, что в течение одной минуты абонент позвонит на коммутатор, равна 0,04. Какова вероятность того, что в течение минуты на коммутатор позвонит а)12 абонентов; б) от 20 до 40 абонентов. Дан ряд распределения случайной величины Х. а)Найти значение *; б) изобразить полигон распределения; в) найти и изобразить графически функцию распределения; г )найти вероятность того, что случайная величина Х примет значение в интервале [3,5; 7,5); д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5); е) найти математическое ожидание случайной величины Х; ж) найти дисперсию случайной величины Х;
Даны законы распределения двух случайных величин Х и Y: Найти закон распределения случайных величин а )Z=X+Y; б)U=XY.
Случайная величина Х задана функцией плотности распределения 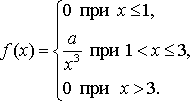 Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал . Постройте графики функций распределения и плотности распределения . Вариант 29 А). Сколько перестановок можно получить из букв слова КУЧЕР? Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов? А). Сколько перестановок можно получить из цифр числа 19438452919? Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов? Из букв слова ПИОНЕР составляются пятибуквенные слова. А).Сколько таких слов можно получить? Б) Сколько таких слов начинается с буквы П? В) А если слова содержат не менее 5 букв? Решить уравнение
В конкурсе мисс ИжГТУ участвовало 13 девушек. Среди них было 6 блондинок и 7 брюнеток. Первокурсник ИВТ факультета пригласил в кино их всех, но пришли только 5 девушек. Найти вероятность того, что первокурсник смотрел кино а) 5 блондинками ; б) двумя блондинками и тремя брюнетками. На отрезок АВ длиной 15 см наугад ставят точку М. Найдите вероятность того, что площадь квадрата, построенного на отрезке АМ, будет заключена между 36 см2 и 81 см2. В специализированную больницу поступают в среднем 50% больных с заболеванием А, 30% — с заболеванием В, 20% — с заболеванием С. Вероятность полного излечения болезни А равна 0,7; для болезней В и С эти вероятности соответственно равны 0,8 и 0,9. Больной, поступивший в больницу, был выписан здоровым. Найдите вероятность того, что этот больной страдал заболеванием В. Игральная кость подбрасывается 8 раз. Найти вероятность того, что а) шестерка выпадет 4 раза; б) шестерка выпадет более четырех раз; в) шестерка выпадет не более шести раз. Аппаратура содержит 2000 одинаковых надежных элементов, вероятность отказа для каждого из которых равна 0,0005. Какова вероятность отказа аппаратуры, если он наступает при отказе хотя бы одного из элементов? Фирма раскладывает листовки с рекламой своего товара по почтовым ящикам. Вероятность того, что реклама сработает и обладатель такой листовки пойдет в магазин и купит товар равна 0,001. Фирма распространила 500 листовок. Найти вероятность того, что пойдут покупать товар этой фирмы а) 25 человек; б) от 200 до 250 человек. Дан ряд распределения случайной величины Х. а)Найти значение *; б) изобразить полигон распределения; в) найти и изобразить графически функцию распределения; г )найти вероятность того, что случайная величина Х примет значение в интервале [3,5; 7,5); д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5); е) найти математическое ожидание случайной величины Х; ж) найти дисперсию случайной величины Х;
Даны законы распределения двух случайных величин Х и Y: Найти закон распределения случайных величин а )Z=X+Y; б)U=XY.
Случайная величина Х задана функцией плотности распределения |