Методические указания к Типовому расчету. Методические указания к Типовому расчету ВАЖНАЯ ХУЙНЯ. ижевский государственный технический университет
 Скачать 1.52 Mb.
|
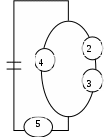
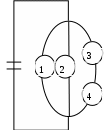
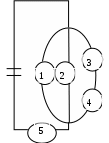
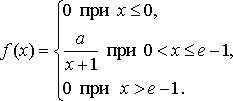 Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал . Постройте графики функций распределения и плотности распределения . Вариант 21 А). Сколько перестановок можно получить из букв слова ОРХИДЕЯ? Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов? А). Сколько перестановок можно получить из цифр числа 4756349845? Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов? Из букв слова ПОЧИНКА составляются пятибуквенные слова. А).Сколько таких слов можно получить? Б) Сколько таких слов начинается с буквы П? В) А если слова содержат не менее 5 букв? Р  ешить уравнение 
В ящике содержится 10 лампочек, среди которых 3 лампы по 60 ватт, а остальные по 100 ватт. Определить вероятность того, что среди наудачу отобранных 6 лампочек окажется а) ровно две 60 ваттные лампы; б) не более двух 60 ваттных ламп. Улитка переползает тропинку за 6 минут. Какова вероятность того, что улитка заметит ползущего по тропинке жука, если она может это сделать лишь в том случае, когда жук находится не более чем в двух минутах до пересечения курса улитки, или не более чем в двух минутах после пересечения жуком курса улитки. Курс жука перпендикулярен курсу улитки. В специализированную больницу поступают в среднем 50% больных с заболеванием А, 30% — с заболеванием В, 20% — с заболеванием С. Вероятность полного излечения болезни А равна 0,7; для болезней В и С эти вероятности соответственно равны 0,8 и 0,9. Больной, поступивший в больницу, был выписан здоровым. Найдите вероятность того, что этот больной страдал заболеванием А. Транзисторный радиоприемник смонтирован на 6 полупроводниках, для которых вероятность брака равна 0,1. приемник отказывает при наличии не менее двух бракованных полупроводников. Найти вероятность того, что: а) откажут ровно 5 полупроводников; б) приемник будет работать; в) приемник откажет. Пусть вероятность того, что пассажир опоздает к отправлению поезда, равна 0,02. Найдите число наиболее вероятное число опоздавших из 855 пассажиров. Какова вероятность того, что опоздает меньше 5 пассажиров? В цехе имеется 90 станков, работающих независимо друг от друга. Для каждого станка вероятность быть включенным равна 0,9. Вычислите вероятность того, что в некоторый момент времени включенными окажутся а) ровно 50 станков; б) от 60 до 75 станков. Дан ряд распределения случайной величины Х. а)Найти значение *; б) изобразить полигон распределения; в) найти и изобразить графически функцию распределения; г )найти вероятность того, что случайная величина Х примет значение в интервале [3,5; 7,5); д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5); е) найти математическое ожидание случайной величины Х; ж) найти дисперсию случайной величины Х;
Даны законы распределения двух случайных величин Х и Y: Найти закон распределения случайных величин а )Z=X+Y; б)U=XY.
Случайная величина Х задана функцией плотности распределения  Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал  . Постройте графики функций распределения и плотности распределения .Вариант 22 А). Сколько перестановок можно получить из букв слова ОРГАНИЗМ? Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов? А). Сколько перестановок можно получить из цифр числа 2948576488? Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов? Из букв слова ПОДХАЛИМ составляются пятибуквенные слова. А).Сколько таких слов можно получить? Б) Сколько таких слов начинается с буквы П? В) А если слова содержат не менее 5 букв? Решить уравнение 
Мама испекла десять пирожков с начинкой. Внешне пирожки были одинаковые. Среди десяти пирожков четыре были с мясом, а остальные с капустой. Определить вероятность того, что среди взятых наудачу пяти пирожков окажется а)три мясных; б) не более трех капустных . Королева Елизавета велела белошвейке вышить на ленте длины а две розы. Найти вероятность того, что расстояние между розами окажется меньше а/4. В первой урне находится один белый и 9 черных шаров, а во второй — один черный и 5 белых шаров. Из каждой урны удалили случайным образом по одному шару, а оставшиеся шары ссыпали в третью (свободную) урну. Найдите вероятность того, что шар, вынутый из третьей урны, окажется белым. Радиоэлектронный комплекс самолета-бомбардировщика включает в себя 8 объектов. Вероятность работы каждого объекта равна 0,9. Объекты выходят из строя независимо один от другого. Найти вероятность того, что : а) откажет хотя бы один объект; б) откажут ровно шесть объектов; в) откажут не менее шести объектов. Найдите вероятность того, что среди 200 изделий окажется не более трех бракованных, если в среднем бракованные изделия составляют 1%. Вероятность изготовления детали со стандартными размерами равна 0,8. Вычислите вероятность того, что среди 300 деталей стандартными будут от 200 до 250. Дан ряд распределения случайной величины Х. а)Найти значение *; б) изобразить полигон распределения; в) найти и изобразить графически функцию распределения; г )найти вероятность того, что случайная величина Х примет значение в интервале [3,5; 7,5); д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5); е) найти математическое ожидание случайной величины Х; ж) найти дисперсию случайной величины Х;
Даны законы распределения двух случайных величин Х и Y: Найти закон распределения случайных величин а )Z=X+Y; б)U=XY.
14.Случайная величина Х задана функцией плотности распределения 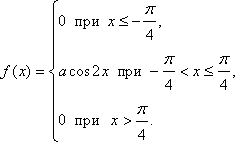 Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал  . Постройте графики функций распределения и плотности распределения .Вариант 23 А). Сколько перестановок можно получить из букв слова НАТУРЩИК? Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов? А). Сколько перестановок можно получить из цифр числа 48375637558 ? Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов? Из букв слова ПЛОТИНА составляются пятибуквенные слова. А).Сколько таких слов можно получить? Б) Сколько таких слов начинается с буквы П? В) А если слова содержат не менее 5 букв? Решить уравнение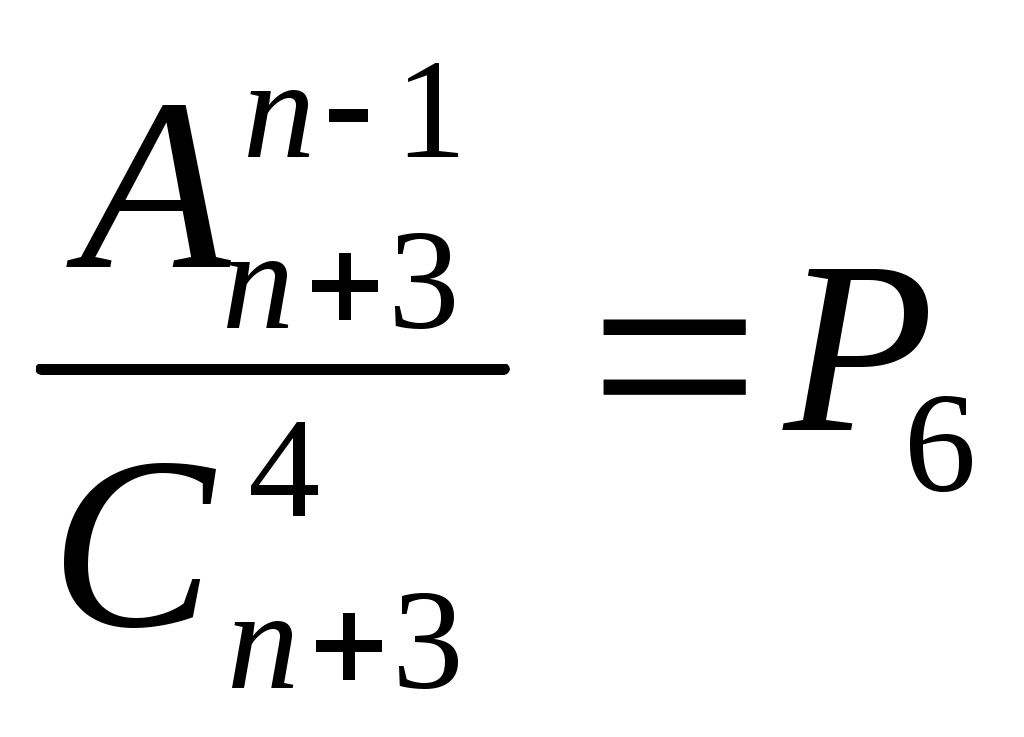 
В вазе стояло 12 цветов : 7 розовых роз и 5 желтых тюльпанов. Наудачу взяли 5 цветов. Определить вероятность того, что желтых тюльпанов среди них будет а) ровно 2 штуки; б) не более двух. В четырехугольник с вершинами в точках (−2 ,2 ) ; (2, 2) ; (2,-2) ; (-2,-2) наудачу брошена точка (х , у ) . Найти вероятность того, что координаты точки удовлетворяют неравенству у - х ≤ 1. Из 2 близнецов первым родился мальчик. Какова вероятность, что вторым родится тоже мальчик, если среди близнецов вероятность рождения 2 мальчиков и 2 девочек соответственно равна 0.6 и 0.4, а для разнополых близнецов вероятность родиться первым для обоих полов одинакова? Наблюдениями установлено, что в некоторой местности в июле в среднем бывает 12 дождливых дней. Какова вероятность того, что из восьми случайно выбранных в этом месяце дней а ) ровно пять окажутся дождливыми; б) дождливыми окажутся хотя бы четыре дня; в) дождливыми будут не более 6 дней? Найдите вероятность того, что среди 200 изделий окажется более трех бракованных, если в среднем бракованные изделия составляют 1%. Вероятность, что рост человека находится в интервале от 164 до 174 равна 0,8. а) Найдите вероятность того, что среди встретившихся вам на улице 300 человек рост ровно 125 человек не будет находиться в интервале от 164 до 174.б) Найдите вероятность того, что среди встретившихся вам на улице 300 человек будут от 120 до 250 человек, чей рост находиться в интервале от 164 до 174. Дан ряд распределения случайной величины Х. а)Найти значение *; б) изобразить полигон распределения; в) найти и изобразить графически функцию распределения; г )найти вероятность того, что случайная величина Х примет значение в интервале [3,5; 7,5); д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5); е) найти математическое ожидание случайной величины Х; ж) найти дисперсию случайной величины Х;
Даны законы распределения двух случайных величин Х и Y: Найти закон распределения случайных величин а )Z=X+Y; б)U=XY.
Случайная величина Х задана функцией плотности распределения |
={элемент k работает}; С={ в цепи нет разрыва}. Выразить события 
и 
через события 
.
