Методические указания к Типовому расчету. Методические указания к Типовому расчету ВАЖНАЯ ХУЙНЯ. ижевский государственный технический университет
 Скачать 1.52 Mb. Скачать 1.52 Mb.
|
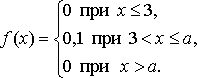 Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал (2; 5) . Постройте графики функций распределения и плотности распределения . Вариант 6 А). Сколько перестановок можно получить из букв слова СВЁРТОК ? Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов? А). Сколько перестановок можно получить из цифр числа 475674658? Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов? Из букв слова ПРИМОЧКА составляются пятибуквенные слова. А).Сколько таких слов можно получить? Б) Сколько таких слов начинается с буквы П? В) А если слова содержат не менее 5 букв? Решить уравнение
Из 10 студентов 6 имеют спортивные разряды. Найти вероятность того, что среди выбранных наудачу 5 студентов спортивный разряд имеют а)3 человека; б) менее трех человек. На отрезок АВ длиной 12 см наугад ставят точку М. Найдите вероятность того, что площадь квадрата, построенного на отрезке АМ, будет заключена между 36 см2 и 81 см2. На радиозаводе машина А производит 40% всех радиостанций, а машина В — 60%. В среднем 9 единиц из 1000 единиц продукции, произведенных машиной А, оказывается браком, а у машины В — брак 2 единицы из 500. Некоторая радиостанция, выбранная случайным образом из дневной продукции, оказалась браком. Какова вероятность того, что она произведена на машине В? Баскетболист делает 5 бросков мячом в корзину. Вероятность попадания мяча при каждом броске одинакова и равна 0,4. найти вероятность того, что а) баскетболист ровно 4 раза попадет мячом в корзину; б) попаданий в корзину будет менее четырех; в) попаданий мячом будет не более 5. Вероятность попадания в цель при каждом выстреле равна 0,001. Найдите вероятность попадания в цель двумя и более выстрелами при залпе в 5000 выстрелов. При штамповке металлических клемм получается в среднем 90% годных. Найдите вероятность того, что среди 900 клемм окажется от 700 до 820 годных. Дан ряд распределения случайной величины Х. а)Найти значение *; б) изобразить полигон распределения; в) найти и изобразить графически функцию распределения; г )найти вероятность того, что случайная величина Х примет значение в интервале [3,5; 7,5); д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5); е) найти математическое ожидание случайной величины Х; ж) найти дисперсию случайной величины Х;
Даны законы распределения двух случайных величин Х и Y: Найти закон распределения случайных величин а )Z=X-Y; б)U=XY.
Случайная величина Х задана функцией плотности распределения  Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал ( Вариант 7 А). Сколько перестановок можно получить из букв слова ТЕРМОС? Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов? А). Сколько перестановок можно получить из цифр числа 384576985? Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов? Из букв слова ПРИРОСТ составляются пятибуквенные слова. А).Сколько таких слов можно получить? Б) Сколько таких слов начинается с буквы П? В) А если слова содержат не менее 5 букв? Решить уравнение
В лотерее «Спортлото 6 из 30» участник лотереи, правильно угадавший 4, 5 или 6 видов спорта из 30 , получает денежный приз. Найти вероятность того, что данный участник угадает а) 5 видов спорта; б) получит денежный приз. Какова вероятность того, что сумма двух наугад взятых положительных чисел, каждое из которых не больше двух, не превзойдет двух, а их произведение будет не больше 2/5 ? В группе из 20 стрелков имеются 4 отличных, 10 хороших и 6 посредственных стрелков. Вероятность попадания в цель при одном выстреле для отличного стрелка равна 0,9, для хорошего — 0,7, для посредственного — 0,5. Найдите вероятность того, что: а) наудачу выбранный стрелок попадет в цель; б) 2 наудачу выбранных стрелка попадут в цель.в) Цель поражена. Найти вероятность, что ее поразил хороший стрелок Среди коконов некоторой партии 30% цветных. Какова вероятность того, что среди 10 отобранных коконов а) цветных будет 3 кокона; б) цветных коконов будет не менее семи; в) цветных коконов будет не более 8. На базе получено 10000 электроламп. Вероятность того, что в пути лампа разобьется, равна 0,0003. Найдите вероятность того, что среди полученных ламп будет пять ламп разбито. Вероятность случайным образом отобранному изделию оказаться стандартным равна 0,8. Найдите вероятность того, что среди 225 взятых наугад изделий а) 180 окажутся стандартными; б) Стандартными окажутся от 155 до 200 изделий. Дан ряд распределения случайной величины Х. а)Найти значение *; б) изобразить полигон распределения; в) найти и изобразить графически функцию распределения; г )найти вероятность того, что случайная величина Х примет значение в интервале [3,5; 7,5); д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5); е) найти математическое ожидание случайной величины Х; ж) найти дисперсию случайной величины Х;
Даны законы распределения двух случайных величин Х и Y: Найти закон распределения случайных величин а )Z=-2X+Y; б)U=XY.
Случайная величина Х задана функцией плотности распределения 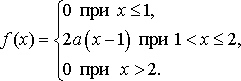 Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал (0,3 ; 1,4) . Постройте графики функций распределения и плотности распределения . Вариант 8 А). Сколько перестановок можно получить из букв слова ТАНЕЦ? Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов? А). Сколько перестановок можно получить из цифр числа374694634 ? Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов? Из букв слова ПРОБКА составляются пятибуквенные слова. А).Сколько таких слов можно получить? Б) Сколько таких слов начинается с буквы П? В) А если слова содержат не менее 5 букв? Решить уравнение
В аудитории находятся 25 студентов. 10 из них изучают английский язык, а остальные 15 – французский. Случайным образом для уборки территории отбираются 5 студентов. Найти вероятность того, что среди них а) ровно 3 изучают английский язык; б) студентов изучающих французский больше. Точка (c, q) наудачу выбирается из квадрата с вершинами (0,0), (1,0), (1,1), (0,1). Найдите вероятность того, что корни уравнения х2 +сх + q = 0 окажутся действительными и разных знаков? Агентство по страхованию автомобилей разделяет водителей по 3 классам: класс Н1 (мало рискует), класс H2 (рискует средне), класс H3 (рискует сильно). Агентство предполагает, что из всех водителей, застраховавших автомобили, 30% принадлежат к классу 50% — к классу H2 и 20% — к классу H3. Вероятность того, что в течение года водитель класса Н1 попадет хотя бы в одну аварию, равна 0,01, для водителя класса H2 эта вероятность равна 0,02, а для водителя класса H3 — 0,08. Водитель А страхует свою машину и в течение года попадает в аварию. Какова вероятность того, что он относится к классу H2? По каналу связи передается 8 сообщений. Каждое из них независимо от других с вероятностью 0,2 искажается помехами. Найти вероятности следующих событий: а) из 8 событий ровно 5 искажаются помехами; б) искажаются помехами не более половины всех передаваемых сообщений; в) помехами искажается более 6 сообщений. Найдите вероятность того, что среди 200 изделий окажется ровно три бракованных, если в среднем бракованные изделия составляют 1%. В цехе имеется 80 станков, работающих независимо друг от друга. Для каждого станка вероятность быть включенным равна 0,9. Вычислите вероятность того, что в некоторый момент времени включенными окажутся а) ровно 50 станков; б) от 60 до 75 станков. Дан ряд распределения случайной величины Х. а)Найти значение *; б) изобразить полигон распределения; в) найти и изобразить графически функцию распределения; г )найти вероятность того, что случайная величина Х примет значение в интервале [3,5; 7,5); д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5); е) найти математическое ожидание случайной величины Х; ж) найти дисперсию случайной величины Х;
Даны законы распределения двух случайных величин Х и Y: Найти закон распределения случайных величин а )Z=X-2Y; б)U=XY.
Случайная величина Х задана функцией плотности распределения |