Методические указания к Типовому расчету. Методические указания к Типовому расчету ВАЖНАЯ ХУЙНЯ. ижевский государственный технический университет

• Название: ижевский государственный технический университет
• Анкор: Методические указания к Типовому расчету
• Дата: 21.05.2021
• Размер: 1.52 Mb.
• Имя файла: Методические указания к Типовому расчету ВАЖНАЯ ХУЙНЯ.doc
• Тип: Методические указания; #208184
• страница: 4 из 14

Свойства математического ожидания:

1. 
   Математическое ожидание постоянной величины равно самой постоянной .
   
2. 
   Постоянный множитель можно выносить за знак математического ожидания .
   
3. 
   Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий .
   
4. 
   Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых
   

Для описания многих практически важных свойств случайной величины необходимо знание не только ее математического ожидания, но и отклонения возможных ее значений от среднего значения.

Дисперсия случайной величины — мера разброса случайной величины, равная математическому ожиданию квадрата отклонения случайной величины от ее математического ожидания.

.

Принимая во внимание свойства математического ожидания, легко показать что



Казалось бы естественным рассматривать не квадрат отклонения случайной величины от ее математического ожидания, а просто отклонение. Однако математическое ожидание этого отклонения равно нулю. Это объясняется тем, что одни возможные отклонения положительны, другие отрицательны, и в результате их взаимного погашения получается ноль. Можно было бы принять за меру рассеяния математическое ожидание модуля отклонения случайной величины от ее математического ожидания, но как правило, действия связанные с абсолютными величинами, приводят к громоздким вычислениям.

Свойства дисперсии:

1. 
   Дисперсия постоянной равна нулю.
   
2. 
   Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.
   
3. 
   Если x и y независимые случайные величины , то дисперсия суммы этих величин равна сумме их дисперсий.
   

Средним квадратическим отклонением случайной величины (иногда применяется термин «стандартное отклонение случайной величины») называется число равное .

Среднее квадратическое отклонение, является, как и дисперсия, мерой рассеяния распределения, но измеряется, в отличие от дисперсии, в тех же единицах, которые используют для измерения значений случайной величины.

Решение задач:

1) Дана случайная величина Х:

xi	-3	-2	0	1	2
pi	0,1	0,2	0,05	0,3	0,35

Найти М(х), D(X).

Решение:

.

=9 =2,31.

.

2) Известно, что М(Х)=5, М(Y)=2. Найти математическое ожидание случайной величины Z=6X-2Y+9-XY.

Решение: М(Z)=6М(Х)-2М(Y)+9-M(X)M(Y)=30-4+9-10=25.

Пример: Известно, что D(Х)=5, D(Y)=2. Найти математическое ожидание случайной величины Z=6X-2Y+9.

Решение: D(Z)=6² D(Х)-2² D(Y)+0=180-8=172.

Тема 7.

Непрерывные случайные величины

Задача 14

Случайная величина, значения которой заполняют некоторый промежуток, называется непрерывной.

Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f(x) – первая производная от функции распределения F(x).


Плотность распределения также называют дифференциальной функцией. Для описания дискретной случайной величины плотность распределения неприемлема.

Зная плотность распределения, можно вычислить вероятность того, что некоторая случайная величина Х примет значение, принадлежащее заданному интервалу.

Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a, b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b.



Функция распределения может быть легко найдена, если известна плотность распределения, по формуле:


Свойства плотности распределения.
1) Плотность распределения – неотрицательная функция.


2) Несобственный интеграл от плотности распределения в пределах от -  до  равен единице.



Решение задач.

1. Случайная величина подчинена закону распределения с плотностью: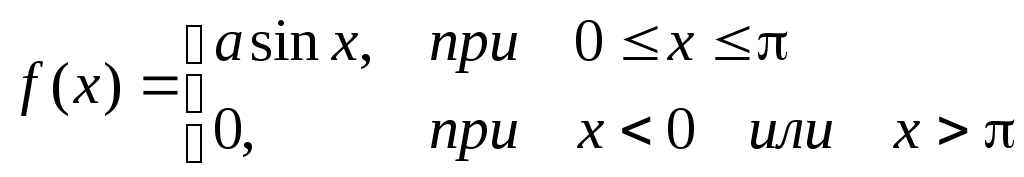


Требуется найти коэффициент а, определить вероятность того, что случайная величина попадет в интервал от 0 до .

Решение:

Для нахождения коэффициента а воспользуемся свойством .




2 .Задана непрерывная случайная величина х своей функцией распределения f(x).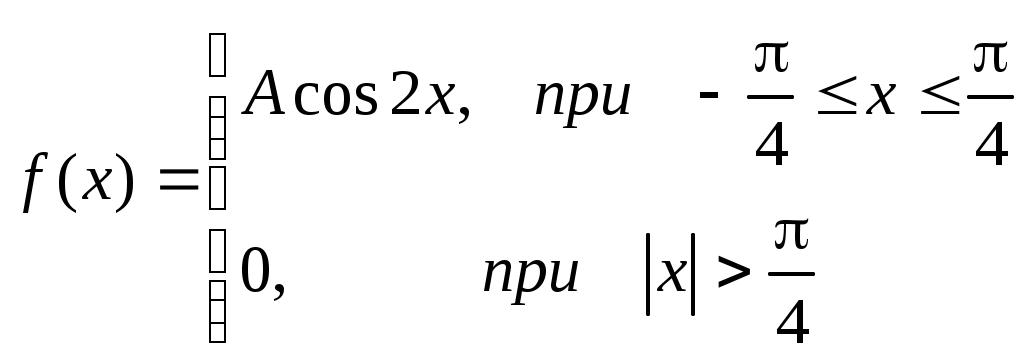



Требуется определить коэффициент А, найти функцию распределения, определить вероятность того, что случайная величина х попадет в интервал .

Решение:

Найдем коэффициент А.


Найдем функцию распределения:

1) На участке :
2) На участке
3) На участке
Итого: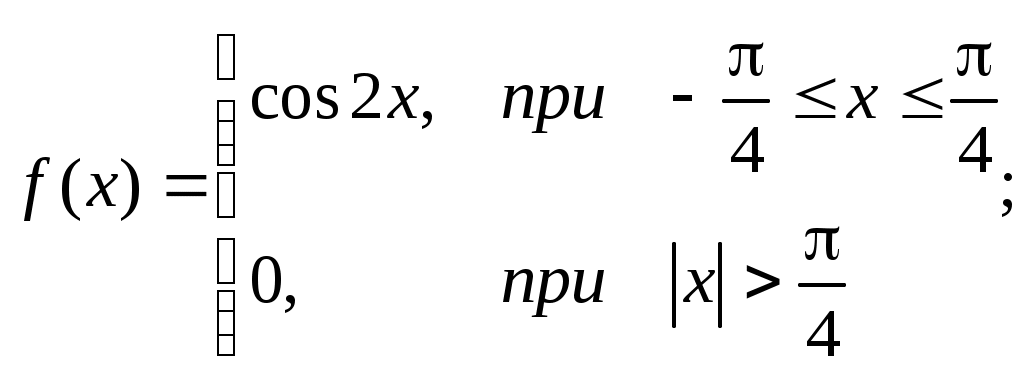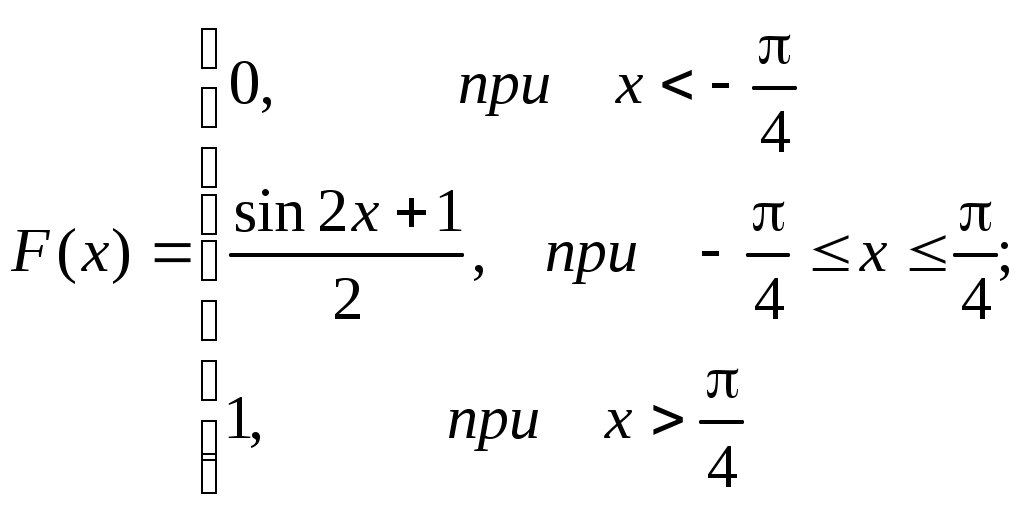
Найдем вероятность попадания случайной величины в интервал .

Ту же самую вероятность можно искать и другим способом:


Вариант 1

1. 
   А). Сколько перестановок можно получить из букв слова ВАЛЕТ ?
   Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?
   

2. 
   А). Сколько перестановок можно получить из цифр числа 125367266?
   Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?
   

3. 
   Из букв слова ПРОГУЛКА составляются пятибуквенные слова.
   А).Сколько таких слов можно получить?
   Б) Сколько таких слов начинается с буквы П?
   В) А если слова содержат не менее 5 букв?
   
   
   
4. 
   Решить уравнение
   

   На рисунке приведена схема электрической цепи. События: ={элемент k работает}; С={ в цепи нет разрыва}. Выразить события и через события и .

5. 
   В ящике содержится 10 деталей, среди которых 3 нестандартные. Определить вероятность того, что в наудачу отобранных 6 деталях окажется а) ровно две нестандартные; б) не более двух нестандартных.
   

7. 
   В круг радиуса R вписан правильный треугольник. Найти вероятность того, что точка, брошенная в круг, попадет в данный треугольник.
   

8. 
   Агентство по страхованию автомобилей разделяет водите­лей по 3 классам: класс Н₁ (мало рискует), класс H₂ (рискует средне), класс H₃ (рискует сильно). Агентство предполагает, что из всех водителей, застраховавших автомобили, 30% принадлежат к классу 50% — к классу H₂ и 20% — к классу H₃. Вероятность того, что в течение года водитель класса Н₁ попадет хотя бы в одну аварию, равна 0,01, для водителя класса H₂ эта вероятность равна 0,02, а для водителя класса H₃ — 0,08. Водитель А страхует свою машину и в течение года попадает в аварию. Како­ва вероятность того, что он относится к классу H1?
   
9. 
   Транзисторный радиоприемник смонтирован на 9 полупроводниках, для которых вероятность брака равна 0,05. приемник отказывает при наличии не менее двух бракованных полупроводников. Найти вероятность того, что: а) откажут ровно 5 полупроводников; б) приемник будет работать; в) приемник откажет.
   

10. 
    Фарфоровый завод отправил на базу 10000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0001. Найдите вероятность того, что на базу придут ровно 3 негодных изделия.
    

11. 
    Известно, что левши составляют примерно 1% . оценить вероятность того, что среди 500 человек окажется а) четверо левшей; б) левшей не менее 80 , но не более 150 человек.
    

12. 
    Дан ряд распределения случайной величины Х.
    а)Найти значение *;
    б) изобразить полигон распределения;
    в) найти и изобразить графически функцию распределения;
    г )найти вероятность того, что случайная величина Х примет значение в интервале
    [3,5; 7,5);
    д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5);
    е) найти математическое ожидание случайной величины Х;
    ж) найти дисперсию случайной величины Х;
    
    
    

xi	2	4	6	7
pi	0,4	0,3	0,1	*

13. 
    Даны законы распределения двух случайных величин Х и Y:
    Найти закон распределения случайных величин а )Z=2X+Y; б)U=XY.
    
    

xi	-1	0	1	2
pi	0,2	0,1	0,3	0,4

yi	-2	0	1	2
pi	0,1	0,2	0,1	0,6

14. 
    Случайная величина Х задана функцией плотности распределения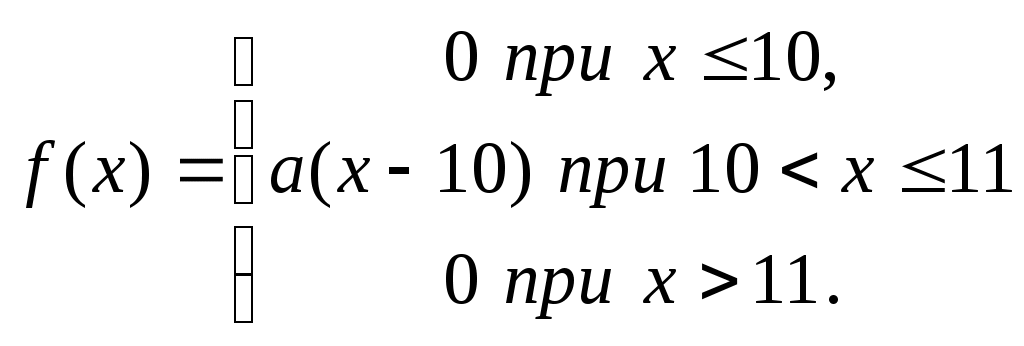
    

Найдите: 1) функцию распределения F(x) и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал (9,15; 10,4) . Постройте графики функций распределения и плотности распределения .
Вариант 2

1. 
   А). Сколько перестановок можно получить из букв слова БОЧКА ?
   Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?
   

2. 
   А). Сколько перестановок можно получить из цифр числа 245752235?
   Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?
   

3. 
   Из букв слова ПРОСЬБА составляются пятибуквенные слова.
   А).Сколько таких слов можно получить?
   Б) Сколько таких слов начинается с буквы П?
   В) А если слова содержат не менее 5 букв?
   
4. 
   Р ешить уравнение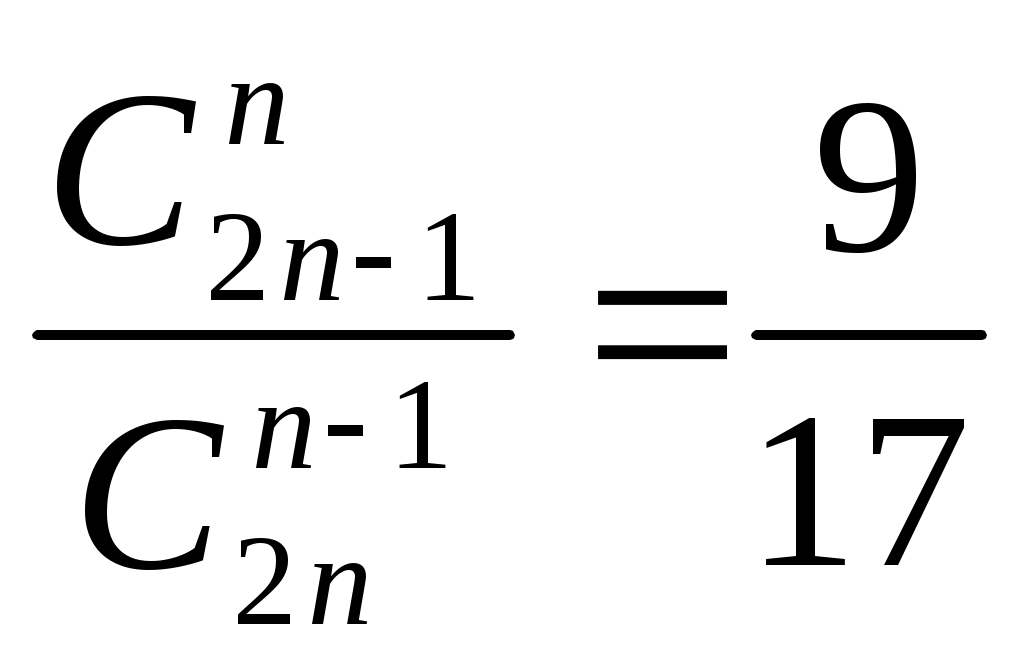
   
5. 
   
   

   На рисунке приведена схема электрической цепи. События: ={элемент k работает}; С={ в цепи нет разрыва}. Выразить события и через события и .

6. 
   Среди десяти билетов выигрышными являются четыре. Определить вероятность того, что среди взятых наудачу пяти билетов окажется а)три выигрышных; б) не более трех выигрышных
   
7. 
   На паркет, составленный из правильных треугольников со стороной а, случайно брошена монета радиуса r. Найдите вероятность того, что монета не заденет границы ни одного из треугольников.
   

8. 
   В студенческом стройотряде 3 бригады первокурсников и одна — второкурсников. В каждой бригаде первокурсников 6 юношей и 4 девушки, а в бригаде второкурсников 4 юношей и 4 девушки. По жеребьевке из отряда выбрали одну из бригад и из нее одного человека для поездки в город, а) Какова вероят­ность того, что выбран юноша? б) Выбранный человек оказался юношей. Какова вероятность, что он первокурсник?
   
9. 
   Радиоэлектронный комплекс самолета-бомбардировщика включает в себя 10 объектов. Вероятность работы каждого объекта равна 0,9. Объекты выходят из строя независимо один от другого. Найти вероятность того, что : а) откажет хотя бы один объект; б) откажут ровно два объекта; в) откажут не менее двух объектов.
   
10. 
    Радиоэлектронный комплекс самолета-бомбардировщика включает в себя 10 объектов. Вероятность работы каждого объекта равна 0,9. Объекты выходят из строя независимо один от другого. Найти вероятность того, что : а) откажет хотя бы один объект; б) откажут ровно два объекта; в) откажут не менее двух объектов.
    

11. 
    Полагая, что вероятность поражения мишени при одном выстреле равна 0,6, найти вероятность того, что а) при 200 выстрелах мишень окажется поражена 110 раз; б) мишень будет поражена от 60 до 140 раз.
    

12. 
    Дан ряд распределения случайной величины Х.
    а)Найти значение *;
    б) изобразить полигон распределения;
    в) найти и изобразить графически функцию распределения;
    г )найти вероятность того, что случайная величина Х примет значение в интервале
    [3,5; 7,5);
    д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5);
    е) найти математическое ожидание случайной величины Х;
    ж) найти дисперсию случайной величины Х;
    
    
    

xi	-1	2	3	4
pi	0,4	0,2	0,1	*

13. 
    Даны законы распределения двух случайных величин Х и Y:
    Найти закон распределения случайных величин а )Z=X+2Y; б)U=XY.
    
    
    

xi	-2	-1	1	2
pi	0,2	0,1	0,3	0,4

yi	-2	0	1	4
pi	0,1	0,2	0,1	0,6

14. 
    Случайная величина Х задана функцией плотности распределения