Методические указания к Типовому расчету. Методические указания к Типовому расчету ВАЖНАЯ ХУЙНЯ. ижевский государственный технический университет
 Скачать 1.52 Mb. Скачать 1.52 Mb.
|
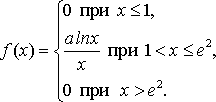 Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал . Постройте графики функций распределения и плотности распределения . Вариант 12 А). Сколько перестановок можно получить из букв слова ДЯТЕЛ? Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов? А). Сколько перестановок можно получить из цифр числа 284757438 ? Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов? Из букв слова ПРИВОЗ составляются пятибуквенные слова. А).Сколько таких слов можно получить? Б) Сколько таких слов начинается с буквы П? В) А если слова содержат не менее 5 букв? Решить уравнение
Среди двенадцати билетов выигрышными являются четыре. Определить вероятность того, что среди взятых наудачу пяти билетов окажется а)три выигрышных; б) не более трех выигрышных . На отрезке АВ длиной а наудачу поставлены две точки С и Д. найти вероятность того, что точка С будет ближе к точке Д, чем к А. На 3 дочерей — Машу, Дашу и Елену — в семье возложена обязанность мыть посуду. Поскольку Маша старшая, ей приходится выполнять 40% всей работы. Остальные 60% работы Даша и Елена делят поровну. Когда Маша моет посуду, вероятность для нее разбить по крайней мере одну тарелку равна 0,02. Для Даши и Елены эта вероятность равна соответственно 0,03 и 0,04. Родители не знают, кто мыл посуду вечером, но они слышали звон разбитой тарелки. Какова вероятность того, что посуду мыла Даша? Радиоэлектронный комплекс самолета-бомбардировщика включает в себя 10 объектов. Вероятность работы каждого объекта равна 0,9. Объекты выходят из строя независимо один от другого. Найти вероятность того, что : а) откажет хотя бы один объект; б) откажут ровно четыре объекта; в) откажут не менее трех объектов. Прядильщица обслуживает 1000 веретен. Вероятность обрыва нити на 1 веретене в течение 1 мин равна 0,003. Вычислите вероятность того, что в течение 1 мин произойдет не более двух обрывов. Вероятность выхода конденсатора из строя в течение времени t равна 0,25. Вычислите вероятность того, что за этот промежуток времени из имеющихся 150 конденсаторов выйдет из строя а) ровно 50 конденсаторов; б) от 40 до 80 конденсаторов. Дан ряд распределения случайной величины Х. а)Найти значение *; б) изобразить полигон распределения; в) найти и изобразить графически функцию распределения; г )найти вероятность того, что случайная величина Х примет значение в интервале [3,5; 7,5); д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5); е) найти математическое ожидание случайной величины Х; ж) найти дисперсию случайной величины Х;
Даны законы распределения двух случайных величин Х и Y: Найти закон распределения случайных величин а )Z=X+Y; б)U=XY.
Случайная величина Х задана функцией плотности распределения  Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал . Постройте графики функций распределения и плотности распределения . Вариант 13 А). Сколько перестановок можно получить из букв слова ГРЕЧИХА ? Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов? А). Сколько перестановок можно получить из цифр числа 574836475 ? Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов? Из букв слова ПРИВЫЧКА составляются пятибуквенные слова. А).Сколько таких слов можно получить? Б) Сколько таких слов начинается с буквы П? В) А если слова содержат не менее 5 букв? Решить уравнение
В букете, состоящем из 10 цветов 6 красных цветка, остальные синие. Наудачу берется 5 цветов. Определить вероятность того, что красных цветов среди них будет а) ровно 2 штуки; б) не более двух. На окружности радиуса R наудачу поставлены три точки А,В и С. Какова вероятность того, что треугольник АВС остроугольный? Известно, что 96% выпускаемых заводом изделий отвечает стандарту. Упрощенная схема контроля признает пригодной стандартную продукцию с вероятностью 0,98 и нестандартную с вероятностью 0,05. Определите вероятность того, что изделие, прошедшее упрощенный контроль, отвечает стандарту. Наблюдениями установлено, что в некоторой местности в июле в среднем бывает 12 дождливых дней. Какова вероятность того, что из восьми случайно выбранных в этом месяце дней а ) ровно четыре окажутся дождливыми; б) дождливыми окажутся хотя бы четыре; в) дождливыми будут не более 7 дней? В зрительном зале находится 400 человек. Какова вероятность того, что среди них имеется 3 левши, если левши в среднем составляют 1%? При штамповке металлических клемм получается в среднем 90% годных. Найдите вероятность того, что среди 900 клемм окажется а) 750 годных; б) от 700 до 820 годных. Дан ряд распределения случайной величины Х. а)Найти значение *; б) изобразить полигон распределения; в) найти и изобразить графически функцию распределения; г )найти вероятность того, что случайная величина Х примет значение в интервале [3,5; 7,5); д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5); е) найти математическое ожидание случайной величины Х; ж) найти дисперсию случайной величины Х;
Даны законы распределения двух случайных величин Х и Y: Найти закон распределения случайных величин а )Z=X+Y; б)U=XY
Случайная величина Х задана функцией плотности распределения 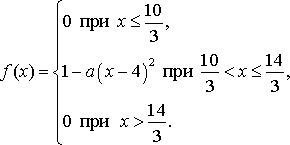 Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал . Постройте графики функций распределения и плотности распределения . Вариант 14 А). Сколько перестановок можно получить из букв слова ГРИМЁР? Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов? А). Сколько перестановок можно получить из цифр числа 3845756475 ? Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов? Из букв слова ПРИМЕТА составляются пятибуквенные слова. А).Сколько таких слов можно получить? Б) Сколько таких слов начинается с буквы П? В) А если слова содержат не менее 5 букв? Решить уравнение
В студенческой группе 12 человек, из которых 5 девушек, а остальные – юноши. Деканат дал студентам этой группы 5 билетов на концерт группы «Тылобурдо». Найти вероятность, что а)3 билета достанутся девушкам; б) не менее трех билетов достанутся девушкам. Два парохода : «Олег Кошевой» и «Быстроходный» должны подойти к одному причалу. Время прихода каждого парохода независимо и равновозможно в течение суток. Найти вероятность того, что одному из пароходов придется ожидать освобождения причала, если время стоянки парохода «Олег Кошевой» один час, а время стоянки «Быстроходного» - два часа. Брак в продукции завода вследствие дефекта А составляет 5%, причем среди забракованной по признаку А продукции 6% имеют дефект В, а в продукции, свободной от дефекта А, дефект В составляет 2%. Найдите вероятность наличия дефекта. Рабочий обслуживает 10 однотипных станков. Вероятность, что станок потребует внимания рабочего в течение промежутка времени Т, равна 1/3. Найти вероятность того, что за время Т а) 4 станков потребуют внимания рабочего; б) менее 2-х станков потребуют внимания рабочего; в) хотя бы 2 станка потребуют внимания рабочего. Завод отправил партию консервов в 2000 штук. Вероятность того, что консервная банка будет разгерметизирована, равна 0,0035. Какова вероятность того, что разгерметизировано будет не более 5 банок консервов? Известно, что дальтоники составляют примерно 2% . оценить вероятность того, что среди 400 человек окажется а) четверо дальтоников; б) дальтоников не менее 80 , но не более 150 человек. Дан ряд распределения случайной величины Х. а)Найти значение *; б) изобразить полигон распределения; в) найти и изобразить графически функцию распределения; г )найти вероятность того, что случайная величина Х примет значение в интервале [3,5; 7,5); д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5); е) найти математическое ожидание случайной величины Х; ж) найти дисперсию случайной величины Х;
Даны законы распределения двух случайных величин Х и Y: Найти закон распределения случайных величин а )Z=X+Y; б)U=XY.
Случайная величина Х задана функцией плотности распределения |