Методические указания к Типовому расчету. Методические указания к Типовому расчету ВАЖНАЯ ХУЙНЯ. ижевский государственный технический университет

• Название: ижевский государственный технический университет
• Анкор: Методические указания к Типовому расчету
• Дата: 21.05.2021
• Размер: 1.52 Mb.
• Имя файла: Методические указания к Типовому расчету ВАЖНАЯ ХУЙНЯ.doc
• Тип: Методические указания; #208184
• страница: 10 из 14

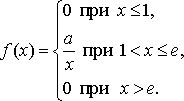Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал . Постройте графики функций распределения и плотности распределения .


Вариант 18

1. 
   А). Сколько перестановок можно получить из букв слова ВОЛЫНКА?
   Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?
   
   
   
2. 
   А). Сколько перестановок можно получить из цифр числа 3857462642?
   Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?
   
   
   
3. 
   Из букв слова ПРОЧЕРК составляются пятибуквенные слова.
   А).Сколько таких слов можно получить?
   Б) Сколько таких слов начинается с буквы П?
   В) А если слова содержат не менее 5 букв?
   
   
   
4. 
   Решить уравнение
   

На рисунке приведена схема электрической цепи. События: ={элемент k работает}; С={ в цепи нет разрыва}. Выразить события и через события и .

6. 
   В аудитории находятся 20 студентов. 12 из них изучают английский язык, а остальные 8 – французский. Случайным образом для уборки территории отбираются 5 студентов. Найти вероятность того, что среди них а) ровно 3 изучают английский язык; б) студентов изучающих французский больше.
   
7. 
   На отрезок АВ длиной 12 см наугад ставят точку М. Найдите вероятность того, что площадь квадрата, построенного на отрезке АМ, будет заключена между 36 см² и 81 см².
   
8. 
   Для сдачи экзамена студентам было необходимо подгото­вить 30 вопросов. Из 25 студентов 10 подготовили все вопросы,8 студентов подготовили по— 25 вопросов, 5 —по 20 вопросов и 2 — по15 вопросов. Вызванный студент ответил на поставленный вопрос. Найдите вероятность того, что этот студент: а) подготовил все вопросы; б) подготовил только половину вопросов.
   
9. 
   По каналу связи передается 8 сообщений. Каждое из них независимо от других с вероятностью 0,1 искажается помехами. Найти вероятности следующих событий: а) из 8 событий ровно 5 искажаются помехами; б) искажаются помехами не более половины всех передаваемых сообщений; в) помехами искажается более 6 сообщений.
   

10. 
    По данным ОТК в среднем 3% изделий требуют дополнительной регулировки. Вычислите вероятность того, что из 200 изделий 4 потребуют дополнительной регулировки.
    

11. 
    Вероятность выхода конденсатора из строя в течение времени t равна 0,3. Вычислите вероятность того, что за этот промежуток времени из имеющихся 150 конденсаторов выйдет из строя а) ровно 60 конденсаторов; б) от 40 до 80 конденсаторов.
    

12. 
    Дан ряд распределения случайной величины Х.
    а)Найти значение *;
    б) изобразить полигон распределения;
    в) найти и изобразить графически функцию распределения;
    г )найти вероятность того, что случайная величина Х примет значение в интервале
    [3,5; 7,5);
    д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5);
    е) найти математическое ожидание случайной величины Х;
    ж) найти дисперсию случайной величины Х;
    
    
    

xi	-2	1	3	4
pi	0,4	0,2	0,1	*

13. 
    Даны законы распределения двух случайных величин Х и Y:
    Найти закон распределения случайных величин а )Z=X+Y; б)U=XY.
    

xi	-1	0	1	2
pi	0,1	0,1	0,3	0,5

yi	-4	0	2	4
pi	0,1	0,4	0,1	0,2

14. 
    Случайная величина Х задана функцией плотности распределения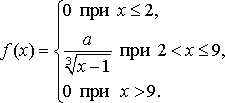
    
15. 
    
    

Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал . Постройте графики функций распределения и плотности распределения .


Вариант 19

1. 
   А). Сколько перестановок можно получить из букв слова ПРОБКА?
   Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?
   
   
   
2. 
   А). Сколько перестановок можно получить из цифр числа 4756473847?
   Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?
   
   
   
3. 
   Из букв слова ПРАВИЛО составляются пятибуквенные слова.
   А).Сколько таких слов можно получить?
   Б) Сколько таких слов начинается с буквы П?
   В) А если слова содержат не менее 5 букв?
   
   
   
4. 
   Решить уравнение
   

   На рисунке приведена схема электрической цепи. События: ={элемент k работает}; С={ в цепи нет разрыва}. Выразить события и через события и .

5. 
   В конкурсе мисс ИжГТУ участвовало 15 девушек. Среди них было 8 блондинок и 7 брюнеток. Первокурсник ИВТ факультета пригласил в кино их всех, но пришли только 5 девушек. Найти вероятность того, что первокурсник смотрел кино а) 5 блондинками ; б) двумя блондинками и тремя брюнетками.
   
6. 
   Внутрь круглого озера радиуса R вписан остров, формой которого является правильный треугольник. Найти вероятность того, что парашютист, выброшенный над озером, упадет в воду.
   

8. 
   Из 2 близнецов первым родился мальчик. Какова вероят­ность, что вторым родится девочка, если среди близнецов вероятность рождения 2 мальчиков и 2 девочек соответственно равна 0.6 и 0.4, а для разнополых близнецов вероятность родиться первым для обоих полов одинакова?
   
9. 
   Игральная кость подбрасывается 9 раз. Найти вероятность того, что а) шестерка выпадет 3 раза; б) шестерка выпадет более трех раз; в) шестерка выпадет не более семи раз.
   

10. 
    Среди семян ржи 0,4% семян сорняков. Какова вероятность при случайном отборе 500 семян обнаружить 5 семян сорняков?
    

11. 
    19) При штамповке металлических клемм получается в среднем 90% годных. Найдите вероятность того, что среди 900 клемм окажется от 700 до 820 годных.
    

12. 
    Дан ряд распределения случайной величины Х.
    а)Найти значение *;
    б) изобразить полигон распределения;
    в) найти и изобразить графически функцию распределения;
    г )найти вероятность того, что случайная величина Х примет значение в интервале
    [3,5; 7,5);
    д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5);
    е) найти математическое ожидание случайной величины Х;
    ж) найти дисперсию случайной величины Х;
    
    
    

xi	2	4	6	7
pi	0,4	0,3	0,1	*

13. 
    Даны законы распределения двух случайных величин Х и Y:
    Найти закон распределения случайных величин а )Z=X+Y; б)U=XY.
    

xi	-2	0	1	2
pi	0,2	0,1	0,2	0,5

yi	-1	0	2	4
pi	0,2	0,2	0,5	0,1

14. 
    Случайная величина Х задана функцией плотности распределения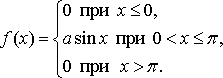
    
15. 
    
    

Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал . Постройте графики функций распределения и плотности распределения .

Вариант 20

1. 
   А). Сколько перестановок можно получить из букв слова ПРИЮТ?
   Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?
   
   
   
2. 
   А). Сколько перестановок можно получить из цифр числа 2847563473?
   Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?
   
   
   
3. 
   Из букв слова ПОХЛЕБКА составляются пятибуквенные слова.
   А).Сколько таких слов можно получить?
   Б) Сколько таких слов начинается с буквы П?
   В) А если слова содержат не менее 5 букв?
   
   
   
4. 
   Решить уравнение _.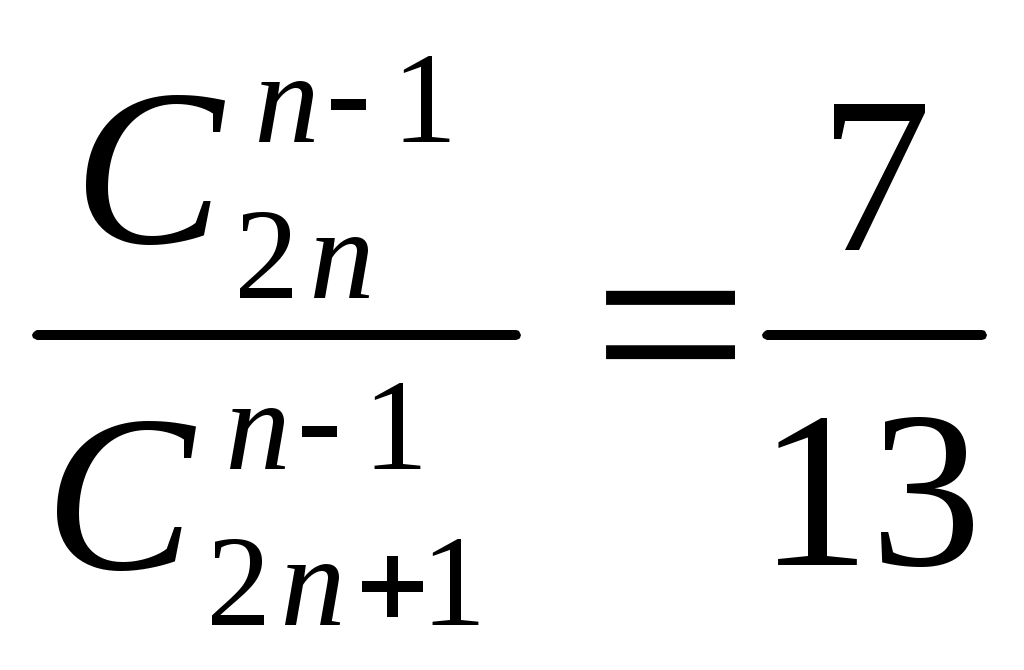
   

На рисунке приведена схема электрической цепи. События: ={элемент k работает}; С={ в цепи нет разрыва}. Выразить события и через события и .

6. 
   У одной одинокой бабушки было 13 кошек. Среди которых были 6 короткошерстных и 7 длинношерстных. На 8 марта одинокая бабушка решила подарить 6 кошечек соседям. Выбирала она их случайным образом. Найти вероятность того, что среди подарочков а) ровно 4 кошки были длинношерстные; б) длинношерстных кошек было не менее четырех.
   
7. 
   Королева Елизавета велела белошвейке вышить на ленте длины а две розы. Найти вероятность того, что расстояние между розами окажется меньше а/2.
   

8. 
   Число грузовых автомашин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых машин, проезжающих по шоссе, как 3 : 2. Вероятность того, что будет заправляться грузовая машина, равна 0,1; для легковой машины эта вероятность равна 0,2. К бензоколонке подъехала машина. Найти вероятность того, что это грузовая машина.
   
9. 
   Монету подбрасывают 9 раз. Какова вероятность того, что герб выпадет: а) три раза; б) не менее трех раз; в) более 6 раз.
   

10. 
    Устройство состоит из 1000 элементов, работавших независимо один от другого. Вероятность отказа каждого из них в течение времени t равна 0,0025. Найдите вероятность того, что за время t откажут ровно 3 элемента.
    

11. 
    Вероятность случайным образом отобранному изделию оказаться стандартным равна 0,8. Найдите вероятность того, что среди 300 взятых наугад изделий а) 180 окажутся стандартными; б) Стандартными окажутся от 155 до 200 изделий.
    

12. 
    Дан ряд распределения случайной величины Х.
    а)Найти значение *;
    б) изобразить полигон распределения;
    в) найти и изобразить графически функцию распределения;
    г )найти вероятность того, что случайная величина Х примет значение в интервале
    [3,5; 7,5);
    д) Найти вероятность того, что случайная величина не попадет в интервал [3,5; 7,5);
    е) найти математическое ожидание случайной величины Х;
    ж) найти дисперсию случайной величины Х;
    
    
    

xi	0	1	3	5
pi	0,1	0,3	0,1	*

13. 
    Даны законы распределения двух случайных величин Х и Y:
    Найти закон распределения случайных величин а )Z=X+Y; б)U=XY.
    

xi	0	1	2	4
pi	0,1	0,1	0,3	0,5

yi	-2	0	2	4
pi	0,1	0,2	0,1	0,6

14. 
    Случайная величина Х задана функцией плотности распределения
    
15.