ргр. РГР по дисциплине Финансовая математика (2022-2023). Имени В. Г

• Название: Имени В. Г
• Дата: 18.12.2022
• Размер: 0.8 Mb.
• Имя файла: РГР по дисциплине Финансовая математика (2022-2023).docx
• Тип: Документы; #850689
• страница: 16 из 22

12

Будем последовательно дисконтировать все денежные потоки по фор-

муле:
PV<sub>k

</sub> R<sub>k

</sub>1  i_^nk

и считать сумму дисконтированных платежей по формуле:

где
S₀  0 .

S_k S_k1  PV_k

1. 
   _PV
   

_ 2400000

 2400000;

S  0  2400000  2400000

1
 ^0,14 ⁰ 1

_1 _{12 }

2. 
   _PV
   

 


2
_ 500000
 466385,84; S
 2400000  466385,84  2866385,84

 ^0,14 ⁶ 2

_1 _{12 }

 

3. 
   _PV3
   

_ 300000

 ^0,14 ¹²

 261018, 91;

S₃  2866385,84  261018, 91  3127 404, 75

_1 _{12 }

4. 
   _PV
   

 


4
_ 350000
 294107, 73;
S 3127 404, 75  294107, 73  2833297, 02

 ^0,14 ¹⁵ 4

_1 _{12 }

5. 
   PV
   

 


5
_ 350000
 284049,55;
S  2833297, 02  284049,55;  2549247, 47

 ^0,14 ¹⁸ 5

_1  _{12 }

6. 
   PV
   

 


6
_ 350000
 274335,36;
S  2549247, 47  274335,36  2274912,11

 ^0,14 ²¹ 6

_1  _{12 }

7. 
   PV
   

 


7
_ 350000
 264953,38;
S  2274912,11 264953,38  2009958, 73

 ^0,14 ²⁴ 7

_1  _{12 }

8. 
   PV
   

 


8
_ 350000
 255892, 26;
S  2009958, 73  255892, 26  1754066, 47

 ^0,14 ²⁷ 8

_1  _{12 }

9. 
   PV
   

 


9
_ 350000
 247141, 01;
S 1754066, 47  247141, 01  1506925, 46

 ^0,14 ³⁰ 9

_1  _{12 }

10. 
    PV
    

 

_ 350000
 238689, 05;
S  1506925, 46  238689, 05  1268236, 40


10 ^0,14 33 10

_1  <sub>

</sub> 12 _

¹¹⁾ PV₁₁ 



350000

^0,14 ³⁶

 230526,14;

^S11

 1268236, 40  230526,14  1037710, 26

_1  <sub>

</sub> 12 _

¹²⁾ PV₁₂ 



350000

^0,14 ³⁹

 222642,39;

^S12

 1037710, 26  294107, 73  815067,87

_1  <sub>

</sub> 12 _

¹³⁾ PV₁₃ 



350000

^0,14 ⁴²

 215028, 26;

^S13

 815067,87  215028, 26  600039, 61

_1  _{12 }

14. 
    PV
    

 

_ 350000
 207674,52;
S  600039, 61  207674,52  392365,10


14 ^0,14 45 14

_1  _{12 }

14. 
    PV
    

 

_ 350000
 200572, 27;
S  392365,10  200572, 27  191792,82


15 ^0,14 48 15

_1  _{12 }

 

¹⁶⁾ PV₁₆ 



350000

^0,14 ⁵¹

 193712,91;

^S16

 191792,82 193712,91  1920, 09  0

_1  _{12 }

 

Таким образом, на 16 шаге расчетов мы получили положительное значе-

ние накопленного NPV . Значит, период окупаемости равен ^{n16  51} месяц или 17 кварталов (меньше 6 лет).

Такое значительное однотипных расчетов лучше проводить с использо-

ванием MS Excel. Внесем (в т.ч. с использованием протаскивания) данные фи- нансовой операции в столбцы Excelтаблицы. Дисконтируем значения денеж- ных потоков. Организуем расчет накопленной суммы. Результаты расчетов и используемые формулы приведены на рисунках ниже.

Как видно из таблицы, накопленный NPVстановится положительным

на 17 квартал или 51 месяц.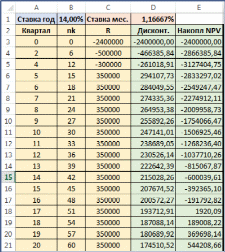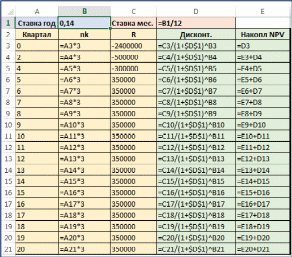

Кредитные расчеты

Кредит – одна из наиболее распространенных современных финансовых операций. При расчетах кредитных операций представляют интерес такие ве- личины, как выплаты в каждый период при известной общей сумме кредита; сумма кредита при заданном лимите на периодические выплаты и др.

Различают операции постнумерандо – когда выплаты производятся в конце периодов пользования займом (классические схемы кредита) и прену- мерандо – когда выплаты производятся вначале периодов пользования займом (аренда, лизинг и т.п.). В этом пособии будем рассматривать только операции постнумерандо. Операции пренумерандо рассмотрены в лекциях.

В данном разделе будут представлены математические формулы, связы- вающие различные параметры кредита и позволяющие определить необходи- мые величины. Будут так же представлены функции MS Excel, реализующие эти формулы.

Заметим, что в реальных операциях кредитования возможны незначи- тельные отличия от параметров, определенных по формулам финансовой ма- тематики. Отличия могут быть обусловлены учетом точного числа дней в ме- сяцах, бонусными днями и т.п. Как правило, такие отличия (особенно при дол- госрочных кредитах) незначительно изменяют искомые величины и тем более не вносят качественных изменений.

Во всех схемах кредитных расчетов каждый k-й платеж R_k

состоит из

начисленных в k-й промежуток времени процентов I_k

и выплаты в погашение

основной части долга

M_k:
R_k I_k

• 
  M_k .
  

Оставшаяся часть основного долга после k-го платежа S_k

ственно понижается:

соответ-

S_k S_k1  M_k.

дита

В начальный момент оставшаяся часть долга равна исходной сумме кре-

S₀  PVC.

Выплаты кредита равными платежами (аннуитет)

Одна из основных схем выплаты кредита – выплата кредита одинако-

выми платежами. В нашей стране за этой схемой закрепилось название «анну- итетная» или «аннуитет». Мы так же будем использовать эту терминологию (хотя в общем случае, «аннуитет» – это синоним слова «рента», то есть любая периодическая схема расчетов).

Таким образом, аннуитет – схема погашения кредита при которой все

периодические платежи одинаковы по величине:

R_k  R const^{. При этом}

^{процентная часть и доля в уплату основного долга меняются:} I_k

растет.

^{падает, а} M_k

Размер аннуитетного платежа определяется по формуле:

_{ j}m q _