ргр. РГР по дисциплине Финансовая математика (2022-2023). Имени В. Г

• Название: Имени В. Г
• Дата: 18.12.2022
• Размер: 0.8 Mb.
• Имя файла: РГР по дисциплине Финансовая математика (2022-2023).docx
• Тип: Документы; #850689
• страница: 13 из 22

_ 

 ^{ } 

То есть, для того, чтобы реальная сумма вклада росла на 7% в год, необ- ходимо, чтобы номинальная ставка была равна 19,34%.

Компенсирующая процентная ставка

^{Компенсирующая процентная ставка} i_ ^{– такая ставка финансовой опе-} рации, которая обеспечивает только компенсацию инфляционного роста цен, то есть при ней реальная доходность равна нулю.

Для долгосрочных вкладов компенсирующая процентная ставка опреде- ляется по формуле:


_ k_

i_ m _1   _^m1_

 

^где i_r<sup>– необходимый годовой уровень доходности; m– число наращений про-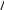

центов в год по вкладу;  – уровень инфляции, который соответствует</sup> 1 k

года.

Пример

(НАМЕК: пример похож на задание 5)

Какой должна быть ставка в банке для предыдущего примера с пенсио- неркой, чтобы она смогла компенсировать рост цен за счет инфляции?

Решение

В этом случае, как уже было рассмотрено ранее, По формуле определяем компенсирующую ставку:

m 3^;

k 4 ^;   0,03 ^.

  ^

k_{ } 4 _

i_ m

_^{1  } ^m1_ ^{ 3 } _^{1  0,03}^{3 1}_ ^{ 0,1206  12,06%}

   

То есть, для того, чтобы данная банковская операция компенсировала инфляционный рост цен, необходимо, чтобы номинальная ставка была равна 12,06%.

Финансовые договоры

Базой составления финансовых договоров и изменения их условий слу- жит понятие эквивалентности схем платежей.

Две схемы платежей считаются эквивалентными, если при приведении (дисконтировании) их на одну дату по определенной договором эффективной ставке доходности операции они дают одинаковый результат.

Из этих же соображений формируются и сами условия выплаты по до- говору. Сумма всех выплат по договору, дисконтированных на дату начала операции, должна быть равна сумме средств, получаемых в долг.

Аналогичный результат дает понятие баланса финансовой операции: сумма всех потоков платежей по финансовому договору, дисконтированных на одну дату по взаимно согласованной процентной ставке, должна быть равна нулю.

^Пусть R_i

^{– платежи по финансовому договору в моменты} n_i

(направле-

ние платежа задается положительным или отрицательным знаком

R_i^{). Со-}

гласно договору определена _j– эффективная процентная ставка его доходно-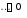

сти. Тогда справедливо соотношение баланса:

B _ ^Ri

_ R₁

• 
  R₂
  

 ^R3 

ⁱ^{1 }

_jⁿ_i^n₀  <sub>1 

j</sub>ⁿ₁^n₀  <sub>1 

j</sub>ⁿ₂ ^n₀  <sub>1 

j</sub>ⁿ₃ ^n₀ 

где ⁿ⁰

– момент времени приведения.

Определение неизвестного параметра финансового договора

Из балансового соотношения можно определить любой один неизвест- ный платеж в рамках финансового договора. Определить его будет проще, если датой приведения выбрать дату этого платежа.

Например, если из 5 платежей неизвестен 4-й, то балансовое соотноше-

ние, приведенное к моменту времени ⁿ₄

будет выглядеть так:

B ^R1

• 
  R₂
  
• 
  R₃
  

 R  ^R5  0

^{1 }

_jⁿ₁ ^n₄  <sub>1 

j</sub>ⁿ₂ ^n₄  <sub>1 

j</sub>ⁿ₃ ^n₄ 

4 ^{1 }

_jⁿ₅ ^n₄ 

Откуда получим:

R   ^R1

_ R<sub>2

</sub> R<sub>3

</sub> R₅

4

Пример

^{1 }

_jⁿ₁ ^n₄  <sub>1 

j</sub>ⁿ₂ ^n₄  <sub>1 

j</sub>ⁿ₃ ^n₄  <sub>1 

j</sub>ⁿ₅ ^n₄ 

(поможет разобраться в задании 8)

Предприятие берет у банка долгосрочный кредит в размере 200 000 000 руб. под 6% годовых. Схема выплаты такова: через 2 года выпла-

чивается 10 000 000 руб.; через 5 лет еще некоторая сумма; завершается опе- рация через 7 лет платежом 8 000 000 руб. Каким должен быть второй платеж, осуществляемый через 5 лет?

Решение

Будем рассматривать ситуацию с точки зрения банка-кредитора. Тогда предоставляемый кредит будет иметь отрицательный знак (деньги уходят из банка), а все остальные платежи будут положительными (деньги приходят в банк). Параметры финансового договора для примера таковы:

j 6%  0,06 ;

R₁  20 000 000 ^;

R₂  10 000 000 ^;

R₃ ^{неизвестно;}

R₄  8 000 000 ^;

n₁  0

(кредит выдается вначале операции);

n₁  2 ^;

n₃  5 ^;

n₄  7 ^.

Приведем все величины к 5-му году и запишем уравнение баланса:


_{B } ^20000000 _10000000 _ R_{3 }8000000 _{ 0}

^{1  0,06}^05^ ^{1  0,06}^25^ ^{1  0,06}^55^ ^{1  0,06}^75^

Тогда:
_{R } ^20000000 _ 10000000 _ 8000000 _{ 7 734 380,03}

³ 1,06^5