ргр. РГР по дисциплине Финансовая математика (2022-2023). Имени В. Г

• Название: Имени В. Г
• Дата: 18.12.2022
• Размер: 0.8 Mb.
• Имя файла: РГР по дисциплине Финансовая математика (2022-2023).docx
• Тип: Документы; #850689
• страница: 12 из 22

30 30

число дней между операциями и поделить на 30, то получится немного другое число).

Так как процентная ставка уже соответствует периоду начисления, ни- каких преобразований для нее делать не нужно.

Наращенная сумма по дробной схеме начисления процентов:

^{FV PV} ^{1  i}n ^{ 400 000 } ^{1  0, 015}467 30 ^{ 504 329,90}

То есть клиентка получит из фонда 504 329 руб. 90 коп. Процент, который получит клиентка, будет равен:

I FV PV 504 329,90  400 000 104 329,90

То есть дополнительно к своей сумме она получит104 329 руб. 90 коп.

Дисконтирование денежных величин

Дисконтированием называют приведение денежных величин к некото- рому заданному моменту времени.

^{Суть операции дисконтирования: известна денежная величина} FV^{в не-} который момент времени (номинальная величина); необходимо определить ее ^{ценность} PV^{на момент приведения (приведенная величина).}

Чаще всего денежные величины приводят к текущему моменту.

Математическое дисконтирование

Математическое дисконтирование – операция, обратная к операции наращения. Она опирается на понятие процентной ставки, определенной как отношение процента к исходной денежной величине:

_i FV PV

PV

В этом случае рассматриваются схемы простого и сложного процента.

Математическое дисконтирование по схеме простого процента

Формула имеет вид:

PV

FV


_1  n i_ ^;

^где PV ^{–дисконтированная (приведенная) величина;} FV ^{– номинальная вели-} чина; i– процентная ставка, отнесенная к расчетному периоду времени (год, квартал, месяц и т.п.); ⁿ– продолжительность времени между моментом при-

ведения и номинальным моментом.

Заметим, что формула простого математического дисконтирования

^{справедлива только для дисконтирования «в прошлое», то есть при} n 0 ^{. Дис-}

контирование «в будущее» реализуется по основной формуле наращения по схеме простых процентов.

Математическое дисконтирование по схеме сложного процента

Формула имеет вид:

PV

FV

_1  i_<sup>n

 FV</sup> ^{1  i}n ^;

^где PV^{– дисконтированная (приведенная) величина;} FV^{– номинальная ве-} личина; i– процентная ставка, отнесенная к расчетному периоду времени (год, квартал, месяц и т.п.); ⁿ– продолжительность времени между моментом

приведения и номинальным моментом.

Формула сложного математического дисконтирования справедлива при

любых ⁿ. При

n 0

она очевидно совпадает с формулой наращения по схеме

сложных процентов.

Банковский учет

Банковский учет – операция, возникшая из необходимости в текущий момент оперировать с ценными бумагами, стоимость которых фиксирована на будущие моменты времени. Она опирается на понятие учетной ставки, опре- деленной как отношение процента к будущей денежной величине:

_i FV PV

FV

^{Часто вместо} i^{для учетной ставки используется обозначение} d ^. Банковский учет всегда предполагает дисконтирование «в прошлое», то

есть

n 0 ^{, величина} FV^{отнесена к моменту более позднему, чем} PV^.

В этом случае также рассматриваются схемы простого и сложного про-

цента.

Банковский учет по схеме простого процента

Формула имеет вид:

PV FV _1  n d_;

^где PV^{– дисконтированная (приведенная) величина;} FV^{– номинальная ве- личина;} d^{– учетная процентная ставка, отнесенная к расчетному периоду} времени (год, квартал, месяц и т.п.); ⁿ– продолжительность времени между

моментом приведения и номинальным моментом.

Заметим, что формула банковского учета с простым процентом справед-

ливо для краткосрочных операций и всегда должно быть

Банковский учет по схеме сложного процента

Формула имеет вид:

n d 1^.

^{PV FV} ^{1  d}n ^;

^где PV^{– дисконтированная (приведенная) величина;} FV^{– номинальная ве- личина;} d^{– учетная процентная ставка, отнесенная к расчетному периоду} времени (год, квартал, месяц и т.п.); ⁿ– продолжительность времени между

моментом приведения и номинальным моментом.

Пример

(НАМЕК: пример похож на задание 6)

За какую сумму можно передать вексель с вексельной суммой 500 000 руб. и сроком платежа через 2 года, если при передаче фиксируется го- довой дисконт 15%. Расчеты провести по всем вариантам дисконтирования.

Решение

Согласно условию, в этой операции

FV 500 000 ^; n 2 ^;

i d 0,15^.

1. 
   Математическое дисконтирование по простому проценту.
   

PV

FV


1  i n

_ 500 000

1  0,15  2

 384 615,38.

2. 
   Математическое дисконтирование по сложному проценту.
   

PV

FV

_1  i_ⁿ

_ 500 000

_1  0,15_²

 378 071,83.

3. 
   Банковский учет по простому проценту.
   

PV FV _1  d  n_  500 000  _1  0,15  2_  350 000, 00 .

4. 
   Банковский учет по сложному проценту.
   

^{PV FV} ^{1  d}n ^{ 500 000 } ^{1  0,15}2 ^{ 361 250, 00 .}

Учет инфляции в финансовых расчетах

Вкладывая деньги в банк или инвестируя в бизнес процессы на некото- рый срок, удается в итоге получить большие суммы. Но за это время цены, как правило, тоже растут. Общий рост среднего уровня цен называется инфля- цией.

Инфляция описывается одним из двух параметров:

• 
  ^{индексом цен} J_ ^{, показывающим, во сколько раз выросли средние}
  

цены за заданный интервал времени;

• 
  уровнем инфляции ^ , показывающим, на сколько процентов вы- росли средние цены за заданный интервал времени.
  

Индекс цен и уровень инфляции, отнесенные к одному моменту вре- мени, связаны простым соотношением:

J_  1  

Реальная наращенная сумма

Пусть за интервал времени ⁿ за счет некоторой финансовой операции ^сумма PV^{наросла до суммы} FV ^{, а индекс цен за этот же интервал равен} J_ ^. Тогда за полученную сумму можно приобрести меньше благ, чем можно было

^{бы сделать в момент начала финансовой операции. Так как цены выросли в} J_

^{раз, то за} FV^{можно приобрести в среднем товаров столько же, сколько} раньше можно было приобрести за

FV<sub>

</sub> FV

J

ции.



Эта величина называется реальной наращенной суммой с учетом инфля-
Индекс цен определяется через уровень инфляции всегда по закону

сложного процента. Если индекс цен соответствует моменту времени ⁿ, а уро- вень инфляции единичному моменту времени, то справедлива формула:



^J ^{1  } n

^{Таким образом, если за время n наращенная сумма стала равна} FV ^{, а} средний уровень инфляции за единичный момент времени равен  , то реаль- ная наращенная сумма определяется по формуле:

FV<sub>

</s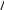ub> FV

_1   _ⁿ

^{Если уровень инфляции соответствует} 1 k^{года, то индекс цен за nлет}

будет равен:



^J ^{1  } k n

тогда реальная сумма определится по формуле:

FV<sub>

</sub> FV

_{1   }kn

Заметим, что при высокой инфляции реальная наращенная сумма может оказаться меньше исходной.

Пример

(пример для общего понимания)

Среднемесячный уровень инфляции в России в первом квартале 2015 года составил 2,42%. Во сколько раз возросли средние цены за первый квар- тал?

Решение


Месячный уровень инфляции по условию задачи равен

_{  2, 42%  0, 0242} . Индекс цен за квартал равен

J _1   _³ , так как в квар-

тале 3 месяца. То есть

J _1  0, 0242_³  1, 074 . То есть средние цены выросли


в 1,074 раза или на 7,4%.

Пример

(НАМЕК: пример похож на часть задания 5)

Предприниматель вложил в бизнес-проект 20 000 000 руб. Через 5 лет

он получил 40 000 000 руб. с которых был вынужден заплатить 15% налогов. Определить реальную наращенную сумму за указанный интервал времени, если среднегодовой уровень инфляции был равен 8%.

Решение

Определим сначала сумму, которую получит предприниматель после выплаты налога:

FV 40 000 000  _1  0,15_  34 000 000 руб.

Годовой уровень инфляции равен   8%  0,08 , число лет гда реальная наращенная сумма будет равна:

n 5^{. То-}

FV_

 ^{34 000 000}  23 139 828, 7 руб.

_1  0, 08_⁵

То есть за 34 000 000 руб. теперь предприниматель сможет приобрести товары примерно в таком количестве, какое можно было приобрести 5 лет назад за 23 139 828 руб. 70 коп.

Реальная процентная ставка

Как видно, за счет инфляции реальные наращенные суммы меньше но- минальных наращенных сумм.

Рассмотрим случай вклада денег в банк под проценты. За счет инфляции оказывается, что вкладчик получает полезность от наращенных сумм мень- шую, чем можно ожидать по номинальной банковской ставке i . Этот эффект ^{учитывается понятием реальнаяпроцентнаяставка}i_r^.

Реальная процентная ставка – это такая величина процентной ставки, при которой вкладчик в той же банковской операции получит реальную нара- щенную сумму.

Если уровень инфляции и период капитализации процентов совпадают, то определить реальную ставку достаточно просто. Действительно, при этом

^{FV PV} ^{1  i}n ^;

FV<sub>

</sub> FV <sub>.

</sub>1   _ⁿ

По определению реальной ставки:

Откуда получаем:

FV_

^{ PV} ^{1  ir}

_n_.

_i 1  i

^r1  

^1.

В общем случае формула для долгосрочных вкладов такова:

 _{1 } ⁱ 

i m ^m 1^

_r _k

^ ^{1  } ^m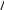

 

где m– число наращений процентов в год по вкладу;  – уровень инфляции, ^{который соответствует} 1 k^{года. Если задан годовой уровень инфляции, то}

k1^.

Пример

(НАМЕК: пример похож на часть задания 5)

Пенсионерка делает вклад в банк в размере 130 000 руб. под 10,5% годо- вых на 2 года с начислением процентов раз в 4 месяца. Ожидаемый уровень инфляции за этот промежуток времени равен 3% в квартал.

Определить реальную наращенную сумму и реальную процентную ставку.

Решение

Определим сначала сумму, которую получит пенсионерка в конце вклада. Так как проценты начисляются раз в 4 месяца, то есть 3 раза в год, то



m 3^{. Число лет} n 2 ^:

_{ i}mn

_ 0,105 _^32

FV PV _1  _m

 130 000  _1 

 159 803,19

3

руб.

   

Определим реальную наращенную сумму. Так как уровень инфляции от-

несен к кварталу, то дет равна:

k 4 ^{(в году 4 квартала). Реальная наращенная сумма бу-}

FV<sub>

</sub> FV <sub>

1   </sub>kn

159 803,19


_1  0, 03_^42

 126 150,11 руб.

В данном случае за счет высокой инфляции пенсионерка получит сумму, позволяющую приобрести товаров в среднем меньше, чем это можно было сделать до вклада.

Определим по формуле реальную процентную ставку:

^ 1  ⁱ

_{  1 } 0,105 _

i m ^m 1^  3  ^3 1^  0,015  1,5%

^r ^{1  } k m ^{ } ^{1  0,03}4 3 ^

   

   

Так как реальная сумма оказалась ниже суммы вклада, то и реальная про- центная ставка оказалась отрицательной.

Обеспечивающая процентная ставка

^{Обеспечивающая процентная ставка} i_o

– такая ставка финансовой опе-

^{рации, которая обеспечивает заданную реальную доходность} i_r^.

Для долгосрочных вкладов обеспечивающая процентная ставка опреде- ляется по формуле:

_ i_r



k_

m
^{io m} _^{1 } _ ^ ^{1  } ^m

_ 

1_



^где i_r<sup>– необходимый годовой уровень доходности; m– число наращений про-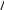

центов в год по вкладу;  – уровень инфляции, который соответствует</sup> 1 k

года.

Пример

(НАМЕК: пример похож на задание 5)

Какой должна быть ставка в банке для предыдущего примера с пенсио- неркой, чтобы она смогла обеспечить реальную доходность не ниже 7% годо- вых? (То есть нужно определить ставку процента, обеспечивающую 7% годо- вых реальной доходности).

Решение

В этом случае, как уже было рассмотрено ранее,

m 3<sup>;

k 4 ;</sup>   0,03 ^.

Требуемая реальная ставка, согласно условию,

определяем обеспечивающую ставку:

i_r 7%  0, 07 . По формуле

_ i_r



k_{ }

0,07 _ ⁴ 

i_o  m _1 _m  _1  _^m1_  3_1 _{3 }  _1 0,03_³ 1_  0,1934  19,34%