ргр. РГР по дисциплине Финансовая математика (2022-2023). Имени В. Г

• Название: Имени В. Г
• Дата: 18.12.2022
• Размер: 0.8 Mb.
• Имя файла: РГР по дисциплине Финансовая математика (2022-2023).docx
• Тип: Документы; #850689
• страница: 8 из 22

2

2. 
   проценты начисляются и капитализируются раз в год, тогда:
   

m1^;

3. 
   проценты начисляются и капитализируются раз в полгода тогда:
   

m ¹

0,5

^{ 2} ;

4. 
   проценты начисляются и капитализируются раз в 4 месяца тогда:
   

m ¹²  3

4

(так как в году 12 месяцев);

5. 
   проценты начисляются и капитализируются раз в квартал тогда:
   

m 4

(так как в году 4 квартала);

6. 
   проценты начисляются и капитализируются раз в месяц тогда:
   

m12

(так как в году 12 месяцев);

7. 
   проценты начисляются и капитализируются раз в 10 дней тогда:
   

m ³⁶⁵  36,5

10

(так как в году 365 дней);

8. 
   проценты начисляются и капитализируются раз в 5 дней тогда:
   

m ³⁶⁵  73

5

(так как в году 365 дней);

9. 
   проценты начисляются и капитализируются раз в день тогда:
   

m 365

(так как в году 365 дней).

В случае 10) используется формула для непрерывного наращения про- центов:

FV PV e^jn

Проведем расчеты для всех случаев:

_{ 0,04 }0,520

1. 
   FV
   

 300 000 000  _1 

0,5 ^

 647 677 499,18 €;

 

_{ 0,04 }120

2. 
   FV
   

 300 000 000  _1  _{1 }

 657 336 942,91 €;

 

_{ 0,04 }220

3. 
   FV
   

 300 000 000  _1  _{2 }

 662 411 899,08 €;

 

_{ 0,04 }320

4. 
   FV
   

 300 000 000  _1  _{3 }

 664 142 064,84 €;

 

_{ 0,04 }420

5. 
   FV
   

 300 000 000  _1  _{4 }

 665 014 565,16 €;

 

_{ 0,04 }1220

6. 
   FV
   

 300 000 000  _1  _{12 }

 666 774 626,09 €;

 


 
_{ 0,04 }36,520

7. 
   FV
   

 300 000 000  _1  _{36,5 }

 667 369 882,37 €;

_{ 0,04 }7320

8. 
   FV
   

 300 000 000  _1 

73 ^

 667 516 011,07 €;

 

9. 
   FV
   

 300 000 000  ^1 

_{0,04 }36520

365 ^

 667 633 013,94 €;

10. 
    
    

 

FV 300 000 000  e^0,0420 


^{667 662 278,55} €.

Заметим, что все расчеты были произведены в MS Excel.

Построим график наращенной суммы в зависимости от числа наращений в год (без учета последнего случая). Для этого сначала составим таблицу:

m	FV
0,5	647 677 499,18
1	657 336 942,91
2	662 411 899,08
3	664 142 064,84
4	665 014 565,16
12	666 774 626,09
36,5	667 369 882,37
73	667 516 011,07
365	667 633 013,94

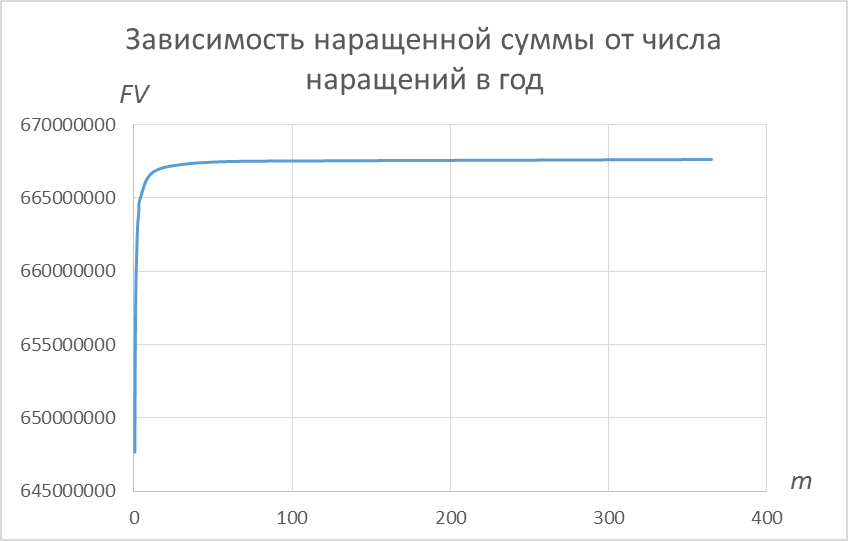и далее в MS Excel по этим данным построим график:

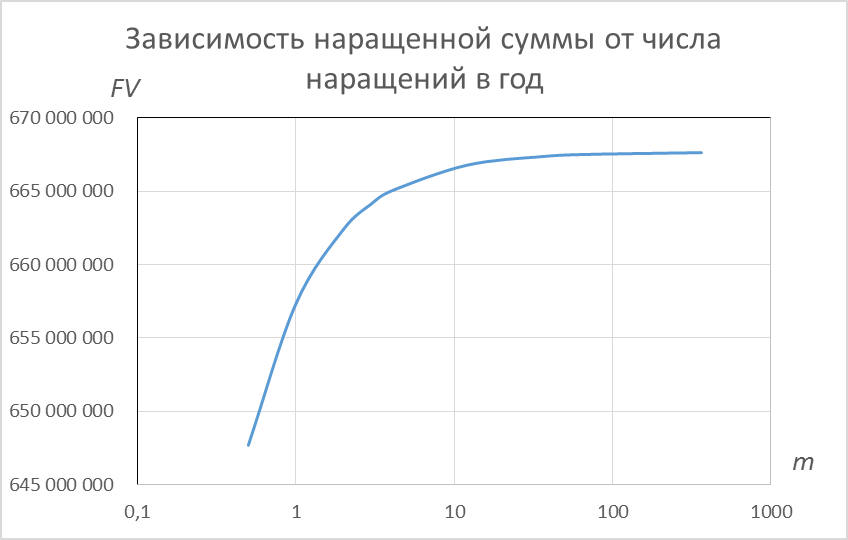В таком виде график не очень нагляден. Гораздо информативнее выгля- дит график с логарифмической шкалой для числа наращений:

Как видно из графика, существенные изменения наращенной суммы ^{происходят примерно до ежемесячных начислений (} m12 ^{). При более частых} начислениях наращенная сумма возрастает уже слабо.

Для примера использования формул расчетов эффективных процентных ставок, рассчитаем случаи 1) – 5) по общей формуле, а случаи 6) – 10) – по частным.

^ 647 677 499,18 ^1 20

1. 
   j_f _
   

300 000 000 ^

1  0,03923  3,923%

 

^ 657 336 942,91 ^1 20

2. 
   
   
   j_f _
   



300 000 000 ^

1  0,04  4%

^ 662 411 899,08 ^1 20

3. 
   j_f _
   

300 000 000 ^

1  0,0404  4,04%

 

^ 664 142 064,84 ^1 20

4. 
   j_f _
   

300 000 000 ^

1  0,04054  4,054%

 

^ 665 014 565,16 ^1 20

5. 
   j_f _
   





300 000 000 ^



0,04 _¹²

1  0,04060  4,06%

6. 
   j_f
   

 _1  _{12 }

1  0,04074  4,074%

 


 
 ^0,04 ^36,5

7. 
   j_f
   

^{ 1 } 36,5 ^

1  0,04079  4,079%

_ 0,04 _⁷³

8. 
   j_f
   

 _1 

73 ^

1  0,04080  4,08%

 

9. 
   j_f
   

 ^1 

0,04 _³⁶⁵

365 ^

1  0,040808  4,081%


 

¹⁰⁾ j_f  e^0,04 1  0,040811  4,081%

Сравнение долгосрочных финансовых операций

Сравнение долгосрочных финансовых операций проводится на основе сравнения их эффективных процентных ставок, определенных для метода сложных процентов. Так как часто финансовые операции не подчиняются

«идеальным» схемам, то лучше использовать общую формулу для определе- ния эффективной годовой процентной ставки:

_{ FV}1 n


PV
j_f _{ } 1

 

^{где в данном случае} PV^{– вложенные коммерсантом средства;} FV^{– сумма,} полученная коммерсантов в конце операции; n– срок операции в годах.

Пример

(НАМЕК: пример похож на задание 7)

Коммерсант рассматривает 4 варианта деятельности:

1. 
   вложить5 300 000 рублей в покупку недвижимости, которую можно будет продать через 3 года за 7 500 000 руб.;
   
2. 
   организовать совместное предприятие, вложив в него 5 000 000 руб. вместе с партнером, доля которого 10 000 000 руб., что позволит по- лучить через 4 года прибыль 24 000 000 руб., которая будет разделена пропорционально первоначальному вкладу;
   
3. 
   закупить товар на 4 000 000 руб. и продать его в течение года за 5 500 000 руб., но заплатив 15% налог с продажи и 200 000 руб. про- давцу;
   
4. 
   вложить 5 000 000 руб. в банк на 2 года под 11% годовых с ежеквар- тальным начислением процентов.
   

Определить, какая схема является наиболее выгодной для коммерсанта с экономической точки зрения.

Решение

Ответ на поставленный вопрос будем давать на основе сравнения эффек- тивных процентных ставок. Так как операции длительные (от года и более), то будем использовать формулы для сложного процента. Так как из возможных схем только одна является стандартной, то лучше использовать общую фор- мулу для определения эффективной годовой процентной ставки:

_{ FV}1 n


PV
j_f _{ } 1

 

^{где в данном случае} PV^{– вложенные коммерсантом средства;} FV^{– сумма,} полученная коммерсантов в конце операции; n– срок операции в годах.

Применим эту формулу для всех возможных вариантов деятельности:

1. 
   В этом варианте
   

PV 5 300 000 ^; FV 7 500 000 ^;

n 3 ^{. Тогда:}

^ 7 500 000 ^1 3


 
^{jf1  } 5 300 000 ^
1  0,1227  12, 27% .

2. 
   ^{В этом варианте} PV 5 000 000 ^; n 4^{. Для определения} FV^надо
   

найти часть прибыли, которую получит коммерсант. По условию, его

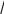
доля равна 5 000 000 _5 000 000 10 000 000_  1 3. Значит, он полу-

чит треть от 24 000 000 руб. то есть 8 000 000 руб. То есть

FV 7 000 000 <sup>. Тогда:

</sup> 8 000 000 ^1 4

 
^{jf2  } 5 000 000 ^

3. 
   В этом варианте
   

1  0,1247  12, 47%.

PV 4 000 000 ^; n1^{. Для определения} FV ^надо

найти прибыль коммерсанта. После выплаты 15% налога с продажи у

^{коммерсанта останется} 5 500 000  5 500 000  0,15  4 675 000 ^руб.

После выплаты зарплаты продавцу у него остается прибыль

4 675 000  200 000  4 475 000

^ 4 475 000 ^11

руб. Тогда:

 
^{jf3  } 4 000 000 ^

1  0,1188  11,88% .

4. 
   ^{В этом варианте} PV 5 000 000 ^; n 2^{. Определим, какую сумму по-}
   

лучит коммерсант из банка через 2 года по формуле сложного про- цента с начислением 4 раза в год (ежеквартально):

_ 0,11 _^42

FV 5 000 000  _1  _{4 }

 6 211 902,76 .

 

Тогда:

^ 6 211 902,76 ^1 2

^jf4 ^ 

5 000 000 ^

1  0,1146  11, 46% .

 

Чем выше годовая эффективная ставка, тем экономически выгоднее ва- риант вложения средств для коммерсанта. Наибольшая годовая эффективная ставка реализуется во втором варианте. Именно его и нужно выбрать коммер- санту.

Комбинированные схемы начисления процентов

Комбинированные схемы наращения используются, как правило, в слу- чае изменения условий операции.

Например, вклад был сделан на 4 года с ежегодным начислением про- центов, но через 2 года и 4 месяца был прерван вкладчиком. Как тогда рассчи- тывать неполный период в 4 месяца? Банки рассчитывают такой период по- особенному, часто – по ставке вкладов до востребования.

Другой пример: заемщик решает погасить взятый на 20 лет кредит через 4 года 3 месяца и 10 дней. Как должен быть рассчитан неполный период (10 дней, если начисления ежемесячные)? Часто этот период рассчитывается по правилу простого процента.

Обычно расчет неполных интервалов осуществляется «не в пользу» того, чьи действия приводят к изменению условий договора. В первом при- мере вкладчик, прерывая договор, получает начисления за неполный период по значительно меньшей процентной ставке, чем прописано в договоре. Во втором случае за неполный период пользования средствами заемщику при- дется заплатить немного больше, чем было бы заплачено по схеме сложного процента.

Так как комбинированные схемы обычно используются не сами по себе, а как вариант расчета прерванных или измененных операций, то интервалы времени рассчитываются обычно от начала операции в полных периодах и по- сле исключения всех полных периодов определяется продолжительность оставшегося интервала в необходимой единице времени.

Например, если основная схема договора имеет интервал расчета квар- тал, то с 13 февраля до 24 октября пройдет:2 квартала с 13 февраля по 13 мая и с 13 мая по 13 августа, и останется еще 72 дня с 13 августа по 24 октября (не забываем, что день открытия и день закрытия операции – это один день).

Наращение по смешанной схеме

При этой схеме наращение за все полные периоды проводится по схеме сложных процентов, а за оставшийся неполный – по схеме простого процента. Формула наращения имеет вид:

^{FV PV} ^{1  i}N ^ ^{1  r i} ^;

I FV PV

^где PV^{– сумма вложенных средств;} FV^{– наращенная сумма;} I^{– проценты;}

i– процентная ставка, отнесенная к расчетному периоду времени (год, квар-

^{тал, месяц и т.п.);} n N r<sup>– продолжительность времени между началом и

концом финансовой операции;</sup> N^{– число целых расчетных периодов между началом и концом операции;} r^{– оставшийся неполный интервал времени} между началом и концом операции, выраженный в долях расчетного периода, ^всегда 0  r1^.

Схема смешанного процента используется чаще всего при прерывании операции заемщиком.

Пример

(НАМЕК: пример похож на часть задания2)

Предприятие берет 22 марта 2016 года кредит в размере 20 000 000 руб. под 8% годовых с ежеквартальным начислением процентов и выплатой в конце 3-х летнего срока.

20 августа 2017 года предприятие хочет полностью рассчитаться за кре- дит. Какова сумма выплаты, если для расчетов используется схема смешан- ного процента?

При расчетах считать, что в полном квартале 91 день.

Решение

Определим полное число кварталов между датами финансовой опера- ции. С 22.03.2016 по 20.08.2017 пройдет 5 полных кварталов:

1) 22.03.16 – 22.06.16;

2) 22.06.16 – 22.09.16;

3) 22.09.16 – 22.12.16;

4) 22.12.16 – 22.03.17;

5) 22.03.17 – 22.06.17.

Следующий полный квартал закончился бы только 22.09.17, то есть позже окончания финансовой операции.

Определим оставшийся неполный интервал времени. Для этого сначала найдем число дней между 22.06.17 и 20.08.17. Между этими датами 59 дней (9 дней в июне, 31 день в июле и 20 дней в августе; минус один день). Значит

^{r 59} .