ргр. РГР по дисциплине Финансовая математика (2022-2023). Имени В. Г

• Название: Имени В. Г
• Дата: 18.12.2022
• Размер: 0.8 Mb.
• Имя файла: РГР по дисциплине Финансовая математика (2022-2023).docx
• Тип: Документы; #850689
• страница: 20 из 22

Пример

(поможет разобраться в ряде пунктов задания10)

Продолжим рассмотрение прошлого примера. Какими будут выплаты фермера, если он возьмет кредит для покупки трактора на тех же условиях, но с дифференцированной схемой погашения?

Решение

Исходные параметры кредитной операции будут такими же, как и для аннуитетной схемы:

PVC 2000000 (исходная сумма кредита);

j 15%  0,15 (номинальная процентная ставка);

m 4 (так как проценты начисляются ежеквартально, то есть 4 раза в год;

^{q 2} (так как выплаты производятся раз в полгода, то есть 2 раза в год);

n 5 (5 лет длится операция).

Ежепериодические выплаты в счет основной суммы будут тогда равны:

M ^PVC ^2000000  200000,00



n q 5  2

Определим ежепериодические выплаты процентов и общие выплаты.

Они будут различны для разных периодов выплат.

Для 1 выплаты ( k 1):

_{ j}mq

^{ }_ 0,15 _^{4 2 }

I₁  S₀  _1 _m

1_  2000000,00  _1  _{4 } 1_  152812,50 ;

_ 

 ^{ } 

R₁  M I₁  200000  152812,50  352812,50 ^;

S₁  S₀  M 2000000  200000  1800000 ^.

То есть из первой выплаты 152 812,50 руб. выплачивается в качестве процентов по кредиту и 200 000,00 руб. – как возврат части основного долга. Итого общая выплата равна 352 812,50 руб. После этой выплаты фермер оста- нется должен 1 800 000 руб.

Для следующих периодов приведем расчеты уже без пояснений. Для 2 выплаты ( k 2):

_{ j}mq

^{ }_ 0,15 _^{4 2 }

I₂  S₁  _1  _m

1_  1800000,00  _1  _{4 } 1_  137531, 25;

_ 

 ^{ } 

R₂  M I₂  200000  152812,50  352812,50 ^;

S₂  S₁  M₂  1800000,00  200000,00  1600000,00 ^.

Для 3 выплаты ( k 3):

_{ j}mq

^{ }_ 0,15 _^{4 2 }

I₃  S₂  _1 _m

1_  1600000,00  _1 _{4 } 1_  122250,00 ;

_ 

 ^{ } 

R₃  M I₃  200000  122250,00  322250,00 ^;

S₃  S₂  M₃  1600000,004  200000,00  1400000,00 ^.

Для 4 выплаты ( k 4):

_{ j}mq

^{ }_ 0,15 _^{4 2 }

I₄  S₃  _1 _m

1_  1400000,00  _1 _{4 } 1_  106968,75;

_ 

 ^{ } 

R₄  M I₄  200000  106968, 75  306968,75 ^;

S₄  S₃  M₄  1400000,00  200000,00  1200000,00 ^.

Для 5 выплаты ( k 5):

_{ j}mq

^{ }_ 0,15 _^{4 2 }

I₅  S₄  _1 _m

1_  1200000,00  _1  _{4 } 1_  91687,50 ;

_ 

 ^{ } 

R₅  M I₅  200000  91687,50  291687,50 ^;

S₅  S₄  M₅  1200000,00  200000,00  1000000,00 ^.

Для 6 выплаты ( k 6):

_{ j}mq

^{ }_ 0,15 _^{4 2 }

I₆  S₅  _1  _m

1_  1000000,00  _1  _{4 } 1_  76406, 25;

_ 

 ^{ } 

R₆  M I₆  200000  76406, 25  276406, 25 ^;

S₆  S₅  M₆  1000000,00  200000,00  800000,00 ^.

Для 7 выплаты ( k 7 ):

_{ j}m q

^{ }_ 0,15 _^{4 2 }

I₇  S₆  _1 _m

1_  800000,00  _1 _{4 } 1_  61125,00 ;

_ 

 ^{ } 

R₇  M I₇  200000  61125,00  261125,00 ^;

S₇  S₆  M₇  800000,00  200000,00  800000,00 ^.

Для 8 выплаты ( k 8 ):

_{ j}mq

^{ }_ 0,15 _^{4 2 }

I₈  S₇  _1  _m

1_  600000,00  _1 _{4 } 1_  45843,75;

_ 

 ^{ } 

R₈  M I₈  200000  45843,75  245843,75 ^;

S₈  S₇  M₈  600000,00  200000,00  400000,00 ^.

Для 9 выплаты ( k 9):

_{ j}mq

^{ }_ 0,15 _^{4 2 }

I₉  S₈  _1  _m

1_  400000,00  _1 _{4 } 1_  30562,50 ;

_ 

 ^{ } 

R₉  M I₉  200000  30562,50  230562,50 ^;

S₉  S₈  M₉  400000,00  200000,00  200000,00 ^.

Для 10 выплаты ( k10):

_{ j}m q

^{ }_ 0,15 _^{4 2 }

I₁₀  S₉  _1  _m

1_  200000,00  _1  _{4 } 1_  15281, 25 ;

_ 

 ^{ } 

R₁₀  M I₁₀  200000  15281, 25  215281, 25 ^;

S₁₀  S₉  M₁₀  200000,00  200000,00  0 ^.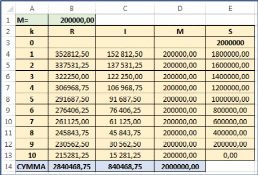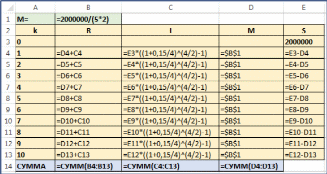



Как и в прошлом случае, проделанные вычисления гораздо быстрее реа- лизуются в MS Excel. Ниже приведены таблицы определенных величин и со- ответствующих формул. Там же сразу сосчитаны суммы выплат.
Как и следовало ожидать сумма выплат по основной части равна исход- ной сумме займа.

В этом случае простая бухгалтерская сумма выплат оказалась меньше, чем для аннуитета. Следует ли из этого вывод, что дифференцированная схема выгоднее для заемщика, чем аннуитет? Ответ на этот вопрос будет дан в сле- дующем подразделе.