ргр. РГР по дисциплине Финансовая математика (2022-2023). Имени В. Г

• Название: Имени В. Г
• Дата: 18.12.2022
• Размер: 0.8 Mb.
• Имя файла: РГР по дисциплине Финансовая математика (2022-2023).docx
• Тип: Документы; #850689
• страница: 18 из 22

j 15%  0,15

(номинальная процентная ставка);

m 4 (так как проценты начисляются ежеквартально, то есть 4 раза в год;

^{q 2} (так как выплаты производятся раз в полгода, то есть 2 раза в год);

n 5 (5 лет длится операция).

_{ j}mq

^{ }_ 0,15 _^{4 2 }

_1  _m

1_{ }1  _{4 }

1_

R PVC ^{  }  2000000  ^{  }  293245,55


_{ j}mn _{ 0,15 }45
1  _1  _m 1  _1  _{4 }
   

То есть каждые полгода фермер должен платить по 293 245,55 руб.

Так как всего будет 10 выплат (5 лет каждые полгода), то простая бух- галтерская сумма выплат будет равна:10  293245,55  2932455,50.

Очевидно, простая бухгалтерская переплата может быть определена как разность между бухгалтерской суммой и исходной суммой кредита. Получим:

2932455,50  2000000  932455,50 .

То есть всего фермер заплатит 2 932 455,50 руб., переплатив по сравне- нию с исходной суммой 932 455,50 руб. (все это без учета изменения ценности денег с течением времени).

Определим выплаты процентов и основной части долга. Они будут раз- личны для разных периодов выплат.

Для 1 выплаты ( k 1):

_{ j}mq

^{ }_ 0,15 _^{4 2 }

I₁  S₀  _1 _m

1_  2000000  _1 _{4 } 1_  152812,50 ;

_ 

 ^{ } 

M₁  R₁  I₁  293245,55 152812,50  140433,05 ^;

S₁  S₀  M₁  2000000 140433,05  1859566,95 ^.

То есть из первой выплаты 152 812,50 руб. выплачивается в качестве процентов по кредиту и только 140 433,05 руб. – как возврат части основного долга. После этой выплаты фермер останется должен 1 859 566,95 руб.

Для следующих периодов приведем расчеты уже без пояснений. Для 2 выплаты ( k 2):

_{ j}mq

^{ }_ 0,15 _^{4 2 }

I₂  S₁  _1  _m

1_  1859566,95  _1  _{4 } 1_  142082,54 ;

_ 

 ^{ } 

M₂  R₂  I₂  293245,55 142082,54  151163,01^;

S₂  S₁  M₂  1859566,95 151163,01  1708403,94 ^.

Для 3 выплаты ( k 3):

_{ j}mq

^{ }_ 0,15 _^{4 2 }

I₃  S₂  _1  _m

1_  1708403,94  _1  _{4 } 1_  130532,74 ;

_ 

 ^{ } 

M₃  R₃  I₃  293245,55 130532,74  162712,81^;

S₃  S₂  M₃  1708403,94 162712,81  1545691,13 ^.

Для 4 выплаты ( k 4 ):

_{ j}m q

^{ }_ 0,15 _^{4 2 }

I₄  S₃  _1  _m

1_  1545691,13  _1  _{4 } 1_  118100, 46 ;

_ 

 ^{ } 

M₄  R₄  I₄  293245,55 118100, 46  175145,09 ^;

S₄  S₃  M₄  1545691,13 175145,09  1370546,04 ^.

Для 5 выплаты ( k 5):

_{ j}mq

^{ }_ 0,15 _^{4 2 }

I₅  S₄  _1  _m

1_  1370546,04  _1  _{4 } 1_  104718, 28;

_ 

 ^{ } 

M₄  R₄  I₄  293245,55 104718, 28  188527, 27 ^;

S₅  S₄  M₅  1370546,04 188527, 27  1182018,77 ^.

Для 6 выплаты ( k 6):

_{ j}mq

^{ }_ 0,15 _^{4 2 }

I₆  S₅  _1  _m

1_  1182018,77  _1  _{4 } 1_  90313,62 ;

_ 

 ^{ } 

M₆  R₆  I₆  293245,55  90313,62  202931,93 ^;

S₆  S₅  M₆  1182018,77  202931,93  979086,84 ^.

Для 7 выплаты ( k 7 ):

_{ j}mq

^{ }_ 0,15 _^{4 2 }

I₇  S₆  _1 _m

1_  979086,84  _1 _{4 } 1_  74808,35 ;

_ 

 ^{ } 

M₇  R₇  I₇  293245,55  74808,35  218437, 20 ^;

S₇  S₆  M₇  979086,84  218437, 2  760649,64 ^.

Для 8 выплаты ( k 8 ):

_{ j}mq

^{ }_ 0,15 _^{4 2 }

I₈  S₇  _1  _m

1_  760649,64  _1  _{4 } 1_  58118,39 ;

_ 

 ^{ } 

M₈  R₈  I₈  293245,55  58118,39  235127,16 ^;

S₈  S₇  M₈  760649,64  235127,16  525522, 48 ^.

Для 9 выплаты ( k 9):

_{ j}m q

^{ }_ 0,15 _^{4 2 }

I₉  S₈  _1  _m

1_  525522, 48  _1  _{4 } 1_  40153, 20 ;

_ 

 ^{ } 

M₉  R₉  I₉  293245,55  40153, 20  253092,35 ^;

S₉  S₈  M₉  525522, 48  253092,35  272430,13 ^.

Для 10 выплаты ( k10):

_{ j}m q

^{ }_ 0,15 _^{4 2 }

I₁₀  S₉  _1  _m

1_  272430,13  _1  _{4 } 1_  20815,36 ;

_ 

 ^{ } 

M₁₀  R₁₀  I₁₀  293245,55  20815,36  272430,19 ^;

S₁₀  S₉  M₁₀  272430,13  272430,19  0,06 ^.

Заметим, что после 10 выплаты сумма долга должна оказаться строго

равной нулю. В данном случае

^S10

оказалась равна минус 6 копейкам из-за

ошибок промежуточных округлений.

Все проделанные вычисления гораздо проще было реализовать с исполь- зованием MS Excel. Ниже приведены таблицы определенных величин и соот- ветствующих формул. Там же сразу сосчитаны суммы выплат процентов и по основному долгу.

Важно, что в MS Excel расчеты проводятся с машинной точностью округления, поэтому остаток долга оказался равным точно нулю.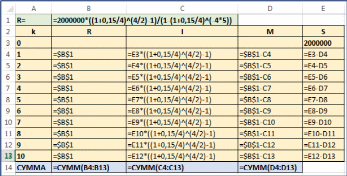

Как и следовало ожидать:

• 
  сумма выплат по основной части равна исходной сумме займа;
  
• 
  простые бухгалтерские суммы общих выплат и выплат процентов оказа- лись равны найденным ранее величинам (с точность до округления).