ргр. РГР по дисциплине Финансовая математика (2022-2023). Имени В. Г

• Название: Имени В. Г
• Дата: 18.12.2022
• Размер: 0.8 Mb.
• Имя файла: РГР по дисциплине Финансовая математика (2022-2023).docx
• Тип: Документы; #850689
• страница: 14 из 22

1,06^3

1,06²

То есть 3-й платеж будет примерно равен 7 734 380 руб.

Пример

(поможет разобраться в задании 8)

Какую сумму может фабрика запросить у банка, если она готова отдать долг двумя платежами: 40 000 000 руб. через 3 года и 50 000 000 руб. через 8 лет? Банк согласен выдать кредит под 8,5% годовых.

Решение

Будем рассматривать ситуацию с точки зрения фабрики. Тогда предо- ставляемый кредит будет иметь положительный знак (деньги приходят на фаб- рику), а все платежи будут отрицательными (деньги уходят). Параметры фи- нансового договора для примера таковы:

j 8,5%  0,085^;

R₁ ^{неизвестно;}

R₂  40 000 000 ^;

R₃  50 000 000 ^;

n₁  0 ^;

n₂  3 ^;

n₃  8 ^.

Так как неизвестна первоначальная сумма кредита, то лучше привести все величины к 0-му году. Запишем уравнение баланса:

B ^R1

_ ^40000000 _ ^50000000 _{ 0}

Тогда:



^{1  0, 085}^00^ ^{1  0, 085}^30^ ^{1  0, 085}^80^

^40000000 ^50000000

R₁  

1, 085³



1, 085⁸

 57 349 796,32

То есть фабрика может получить кредит примерно 57 349 796 руб.

Изменение и сравнение условий финансовых договоров

На основе того же уравнения баланса можно определить параметры из- менений финансового договора.

Для сравнений финансовых договоров можно определить и сравнить их эффективные нормы доходности. Но это сделать технически трудно (если не привлекать MS Excel или другие пакеты программ).

Варианты договоров можно сравнить также на основе определения ба- ланса договора на некоторую любую дату. Определив баланс с учетом дискон- тирования величин по ставке исходного договора, можем сделать два типа вы- водов:

1. 
   Если баланс оказался положительным, то новое условие выгоднее ис- ходного для того участника договора, с точки зрения которого рас- сматриваются знаки потоков платежей. Соответственно, при отрица- тельном балансе для этого участника новый договор менее выгоден.
   

2. 
   Для участника договора, с точки зрения которого рассматриваются знаки потоков платежей, выгоднее тот вариант договора, который приводит к большему значению баланса.
   

Пример

(поможет разобраться в задании 8)

Холдинг, взял кредит в банке в размере 15 000 000 руб. под 14% годовых и должен был рассчитаться по следующей схеме:

через 2 года 10 000 000 руб.

через 4 года 12 338 402 руб.

(Можно проверить, что операция сбалансирована).

Холдинг предлагает банку изменить условие договора и рассчитаться двумя одинаковыми платежами по 11 000 000 руб. через 2 и 3 года от начала операции.

Выгодно ли такое изменение договора банку?

Решение

Составим баланс нового договора с позиции банка. В этом случае пара- метры договора будут равны:

j 0,14 ^;

R₁  15 000 000 ^; R₂  R₃  11 000 000 ^.

n₁  0 ^;

n₂  2 ^;

n₃  3 ^.

В качестве момента приведения можно использовать любую дату. Вы- берем датой приведения момент начала операции.

Баланс договора равен:

B ^R1

• 
  R₂
  

 ^R3 

_1 

_jⁿ₁ ^n₁  <sub>1 

j</sub>ⁿ₂ ^n₁  <sub>1 

j</sub>ⁿ₃ ^n₁ 

_ 15 000 000 _



11 000 000

_ 11 000 000

 888829, 49  0

_1  0,14_^00^ _1  0,14_^20^ _1  0,14_^30^

Так как баланс, составленный с точки зрения банка, оказался положи- тельным, можно сделать вывод, что данное изменение банку выгоднее и банк согласится на предложенный вариант изменения договора.

Пример

(поможет разобраться в задании 8)

Продолжим рассмотрение прошлого примера. Холдинг предлагает банку еще один вариант погашения задолженности: единым платежом 30 000 000 через 5 лет. Какой из вариантов изменения договора выгоднее для банка?

Решение

Составим баланс нового договора с позиции банка. В этом случае пара- метры договора будут равны:

j 0,14 ^;

R₁  15 000 000 ^; R₂  30 000 000 ^.

n₁  0 ^; n₂  5 ^.

Для того, чтобы сравнить варианты, в качестве момента приведения нужно использовать ту же дату, для которой был произведен первый расчет, то есть момент начала операции.

Баланс этого варианта договора равен:

B ^R1

• 
  R₂
  

_ 15 000 000 _

30 000 000

 581059,93  0

^{1 }

_jⁿ₁ ^n₁  _{1 }

^j^n2 n1 ^ ^{1  0,14}^00^ ^{1  0,14}^50^

Как видно из баланса, этот вариант тоже выгоднее исходного договора (так как баланс оказался положительным), но менее выгоден, чем предыдущий ^{вариант изменения (так как} 581059  888829 ^).

Оценка инвестиционных проектов

Инвестиционные проекты будем оценивать только на основе принципа дисконтирования денежных потоков, отнесенных к соответствующим момен- там времени (расходов и доходов, осуществленных в разные моменты вре- мени).

Чистый приведенный доход

При оценке инвестиционных проектов используется метод расчета чи- ^{стого приведенного дохода} NPV^{(net present value), который предусматривает} дисконтирование денежных потоков: все доходы и затраты приводятся к од- ному моменту времени.

Центральным показателем в рассматриваемом методе является показа- тель чистого приведенного дохода – текущая стоимость денежных потоков за вычетом текущей стоимости денежных оттоков.

Обозначим через ^Ik

инвестиции (расходы, затраты) в моменты времени

^nk. Через ^Dk

обозначим доходы (прибыль), полученные в эти же моменты вре-

мени. Некоторые из этих величин могут быть равны нулю. Тогда чистый при- веденный доход определяется по формуле:

NPV _ ^Dk

_ I<sub>k

 </sub>^{Dk Ik}



(NPV1)

k^{1  i}ⁿk

k^{1  i}ⁿk

k^{1  i}ⁿk

В этой формуле i– ставка дисконтирования, отражающая ожидаемый инве- стором уровень доходности финансовой операции.

Часто проще работать в суммарных денежных потоках ^R_k

 D_k

• 
  I_k
  

в мо-

менты времени

ⁿ_k. Тогда:
NPV
_ R_k



_k1  i_^nk
(NPV2)

Таким образом, NPV это приведенная к текущему моменту суммарная стоимость денежных потоков: денежных поступлений за вычетом денежных оттоков.

Если для требуемой инвестором ставки дисконтирования

NPV 0 , то

проект считается выгодным; при

NPV 0

– невыгодным. В крайне редком

случае, когда

NPV 0

говорят о нулевой выгоде проекта.

Пример

(поможет разобраться в задании 9 п.1)

Инвестор рассматривает вариант покупки сельскохозяйственного пред- приятия за 800 000 ¥. Через год предприятие принесет потребует дополнитель- ных затрат на закупку техники 200 000 ¥, доходов не ожидается. Еще через год ожидается безвозмездная государственная дотация в размере 400 000 ¥, но еще будет необходимо затратить 500 000 ¥ на постройку элеватора. Через 3 и 4 года от покупки планируется безубыточная, но и бесприбыльная деятельность. Че- рез 5 лет предприятие принесет прибыль 300 000 ¥, через 6 лет – прибыль 600 000 ¥ и в этот же момент его планируется продать за 1 200 000 ¥.

Определить, выгоден ли описанный вариант покупки для инвестора, если он ожидает доходность на уровне 12% годовых. Будет ли выгодным дан- ный проект, если ожидаемый уровень инвестиций 20%?

Решение

Определим параметры финансовой операции.

^{В момент покупки (} n₁  0 ^{) вносится первоначальная инвестиция}

I₁  800000 ^{, доход в этот момент времени равен} D₁  0 <sup>.

Через год (</sup> n₂  1^{) расходы} I₂  200000 ^, D₂  0 <sup>.

Через 2 года (</sup> n₃  2 ^{) расходы} I₃  500000 ^, D₃  400000 ^.

Через 3 и 4 года затрат и прибыли не ожидается и их в расчетах не отра-

жаем.

^{Через 5 лет (} n₄  5 ^{) инвестиций нет}

I₄  0 ^{, прибыль}

D₄  300000 ^.

^{Через 6 лет (} n₅  6 ^{) инвестиций нет} I₅  0 ^{,доход складывается из годо-}

вой прибыли и суммы продажи:

D₅  600000  1200000  1800000 ^.

Таким образом, формула для определения чистого приведенного дохода запишется так:

NPV

D₁  I₁

^{1  i}n¹

_ D₂  I₂

^{1  i}n²

_ D₃  I₃

^{1  i}n³

_ D₄  I₄

^{1  i}n⁴

_ D₅  I₅

^{1  i}n⁵

Определим чистый приведенный доход при указанных годовых про- центных ставках.

^{1) При} i12%  0,12 ^:

_NPV 0  800000 _ 0  200000 _ 400000  500000 _ 300000  0 _ 1800000  0 _



^{1 0,12}0 ^{1 0,12}1 ^{1  0,12}2 ^{1  0,12}5 ^{1  0,12}6

 800000 178571, 43  79719,39 170228, 06  911936, 02  23873,36

Так как

NPV 0, то проект покупки данного сельскохозяйственного

предприятия следует признать выгодным при требуемой годовой норме при- были 12%.

^{2) При} i 20%  0,2 ^:

_NPV 0  800000 _ 0  200000 _ 400000  500000 _ 300000  0 _ 1800000  0 _



^{1 0, 2}0 ^{1 0, 2}1 ^{1 0, 2}2 ^{1  0, 2}5 ^{1  0, 2}6

 800000 166666, 67  69444, 44 120563, 27  602816,36  312731, 48

Так как

NPV 0 , то проект покупки данного сельскохозяйственного

предприятия следует признать невыгодным при требуемой годовой норме прибыли 20%.

Внутренняя норма доходности

Величина чистого приведенного дохода NPV достаточно проста для вы- числения. Однако недостатком этого понятия является то, что это абсолютная, а не относительная величина.

Например, в части 1) рассмотренного выше примера, мы сделали вывод

о выгодности приобретения сельскохозяйственного предприятия на основе по-

ложительного значения NPV 23873,36 ¥. В то же время, все суммы в задаче

на порядок больше и исчисляются сотнями тысяч, а первоначальная сумма ин- вестиций почти равна миллиону иен. Иногда это может вызвать такое проти- воречие: «как решение об инвестировании сотен тысяч и миллионов может быть принято на основе незначительных положительных значений чистого приведенного дохода?»

Снять это противоречие и сделать анализ инвестиционных проектов еще нагляднее помогает понятие внутренней нормы доходности.

Внутренняя норма доходности IRR(внутренняя ставка доходности, in-

ternal rate of return) – это ставка дисконтирования, приравнивающая сумму приведенных доходов от инвестиционного проекта к величине инвестиций, т.е. ставка, для которой вложения окупаются, но не приносят прибыль. Дру- гими словами, внутренняя норма доходности – это процентная ставка ⁱ при которой величина NPVдля инвестиционной операции равна нулю.

Таким образом, IRRопределяется из уравнения:

NPV _ ^Dk

_ I<sub>k

 </sub> <sup>Dk

 Ik</sup>  _ ^Rk  0

k^{1  IRR}ⁿk

k^{1  IRR}ⁿk

k^{1  IRR}ⁿk

k^{1  IRR}ⁿk

где все обозначения описаны в прошлом подразделе.

Аналитически выразить IRRиз этого уравнения чаще всего невоз- можно. Поэтому величина внутренней нормы доходности определяется обычно с применением компьютерных методов. Используются как правило один из следующих подходов:

1. 
   Подбор параметра. В этом случае реализуется компьютерное вычис- ление NPVпо формул (NPV1) или (NPV2) с возможностью менять ставку i. Ставка подбирается вручную или автоматически так, чтобы NPV  0 . Например, в MS Excel имеются возможности подбора ставки с использованием инструмента «Подбор параметра…» или с использованием средства «Поиск решения».
   
2. 
   Использование стандартных функций пакетов прикладных программ. Например, в MS Excel внутренняя ставка доходности определяется с использованием финансовой функции ВСД.
   

Достоинством первого подхода является его универсальность. Все пара- метры инвестиционной операции могут быть произвольными. Недостаток пер- вого подхода – его сложность.

При простоте использования стандартных функций их использование обычно не универсально. Например, функция ВСД подразумевает, что денеж-

ные потоки отнесены к полным временным интервалам ( n_k

целое), а исполь-

зование денежных потоков в промежуточные моменты времени ( n_k

не предполагается.

не целое)

Вывод о выгодности инвестиционного проекта на основе определения внутренней нормы доходности делается следующим образом. Если IRRбольше требуемого инвестором значения, то проект считается выгодным. Если IRR меньше – то проект рекомендуется отвергнуть. Часто в качестве рубеж- ного значения IRR принимается ставка привлечения финансовых ресурсов CC(Cost of Capital), возможно, с учетом рисков.

Пример

(поможет разобраться в задании 9 п.2)

Определить на основе понятия внутренней нормы доходности, выгоден ли описанный в предыдущем примере вариант покупки сельскохозяйствен- ного предприятия для инвестора, если он ожидает доходность на уровне 12% годовых; 20%?

Решение

Способ 1. Определение с использованием подбора параметра.

Сформируем в MS Excel таблицу моментов времени (ячейки A4:A8), фи- нансовых потоков (ячейки B4:B8) и их дисконтированных величин (ячейки C4:C8) по некоторой ставке, которую будем вводить в ячейку B1. Сумма дис- контированных потоков будет равна NPV (пометим ее в ячейку C9). Таблица и соответствующие формулы приведены на рисунке ниже. Для примера в ячейку B1 введено значение 10%.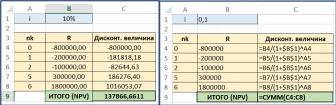





Изменяя значение процентной ставки в ячейке B1 можно добиться нуле- вого значения NPVв ячейке C9. Подбор можно осуществлять вручную. Но лучше воспользоваться инструментарием MS Excel.

Вариант использования инструмента «Подбор параметра…» во вкладке ДАННЫЕ, раздел Работа с данными / Анализ "что если" (см. рис.).





Подбор параметра настраиваем так, чтобы в ячейке C9 оказалось нуле- вое значение за счет изменения значения процентной ставки в ячейке B1 (см. на следующем рисунке):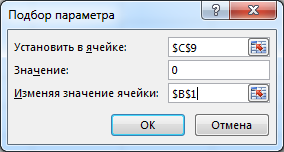




Результат подбора параметра приведен на рисунке ниже: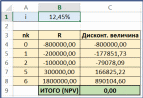

Таким образом, в данной ситуации

^{IRR12, 45%}.

Значит, если инвестор рассчитывает на доходность 12%, то проект вы- годен (^{12, 45% 12%}).

Если инвестор рассчитывает на доходность 20%, то проект невыгоден (так как ^{12, 45%  20%}).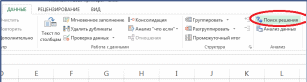

Вариант использования инструмента «Поиск решения» (во вкладке ДАННЫЕ выбирается средство анализа «Поиск решения» (см. рис.)). Данный инструмент должен быть предварительно инициализирован (см., например, по ссылке http://www.excelworld.ru/publ/hacks/tools/solver/27-1-0-122).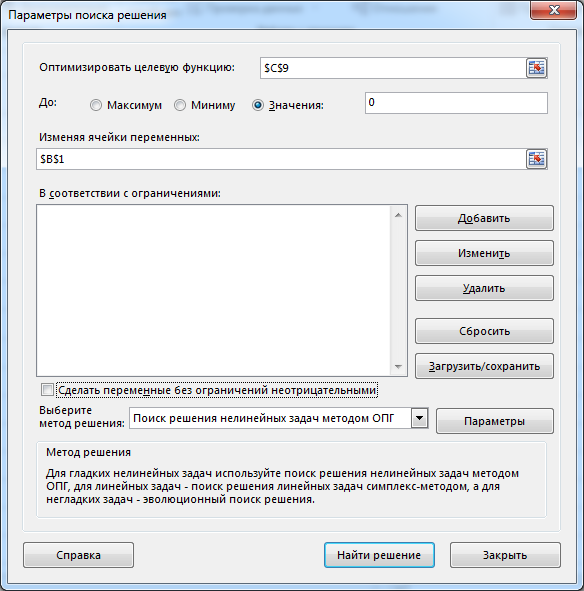

В окне настройки Поиска решения необходимо установить целевую ячейку где находится NPV (ячейка C9); далее установить её требуемое значе- ние (Значение: 0); нужное значение достигается за счет изменения процентной ставки (ячейка B9). Настройка поиска решения приведена на рисунке ниже.

Нажимая «Найти решение» мы получаем тот же результат, что и с помо-

щью инструмента «Подбор параметра»: ^{IRR 12, 45%}.

Заметим, что настройка «Поиска решения» сложнее, чем настройка

«Подбора параметра», но она запоминается системой. Настройку «Подбора параметра» нужно выполнять каждый раз заново.

Способ 2. Определение с использованием функции ВСД.

Функция ВСД относится к финансовым функциям MS Excel. Она пред- полагает задание величин финансовых потоков в каждый период времени при равноотстоящих моментах. Полученная в результате ставка относится к рас- сматриваемому моменту времени. Дробные моменты времени не допуска- ются. Если в определенные моменты времени потоков не было, то нужно явно задать в эти моменты времени нулевые значения потоков.

Сформируем в MS Excel таблицу моментов времени от 0 до 6 (ячейки A2:A8) и финансовых потоков (ячейки B2:B8) в эти моменты времени. В 3 и 4 моменты времени денежные потоки равны нулю.

В ячейку B10 введем функцию ВСД(B2:B8). Заметим, что эта функция не требует задания моментов времени.

Результат работы и использованные формулы приведены ниже на рисун-

ках.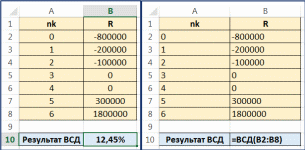





Результат, как и должно быть, совпадает с результатом первого способа:

^{IRR12, 45%}.

Пример

Инвестор рассматривает возможность покупки старой фабрики с целью последующего перепрофилирования и продажи площадей. Предполагаемая цена сделки 23 000 000 руб. Через 1,5 месяца нужно уволить оставшийся пер-

сонал с выплатой выходного пособия в суммарном размере 2 000 000 руб. Че- рез полгода от момента покупки необходимо будет вложить 1 500 000 руб. для оформления документов на перепрофилирование в торговые ряды. После этого в течение 4 месяцев планируется вкладывать по 500 000 руб. на ремонт- ные работы. Через год после покупки нужно будет вложить в рекламу новых образовавшихся торговых рядов 1 200 000 руб. После этого планируется начать распродажу площадей. Ожидаются прибыли от продаж в размере 3 000 000 руб. ежемесячно в течение всего второго года.

При какой годовой ставке привлечения средств будет выгоден данный проект?

Решение

В данной задаче периоды времени отнесены к части года и даже к не- полной части месяца. При этом решение задачи через функцию ВСД невоз- можно (если только не переходить к половине месяца как единичному интер- валу времени). Решим задачу первым способом – через подбор параметра.

^{Определим параметры финансовой операции:} n_k

в годах и соответству-

^ющие R_k

в рублях.

^{В начальный момент (} n₁  0 ^{) планируется вложить в покупку}

15 000 000 руб., то есть

R₁  23000000 ^.

Через полтора месяца ( ^{n 1,5  0,125}) будут снова выплаты: