ргр. РГР по дисциплине Финансовая математика (2022-2023). Имени В. Г

• Название: Имени В. Г
• Дата: 18.12.2022
• Размер: 0.8 Mb.
• Имя файла: РГР по дисциплине Финансовая математика (2022-2023).docx
• Тип: Документы; #850689
• страница: 21 из 22

Аналитическое сравнение схем погашения кредита

При сравнении схем погашения кредита опираются, как правило, на сумму выплат или сумму переплат по кредиту. Однако использовать простую сумму денежных выплат некорректно, особенно для больших сроков кредита. Это обусловлено изменением ценности денег с течением времени.

Наиболее верным с точки зрения финансовой математики и экономиче- ского анализа проводить сравнение суммарных выплат с учетом их дисконти- рования на дату получения кредита. Ставкой дисконтирования при этом выби- рается ставка изменения ценности денег для заёмщика. (Важно заметить: при дисконтировании кредитных выплат по эффективной ставке, указанной в до- говоре кредитования, сумма всегда должна будет быть равна исходной сумме кредита).

Пример

(поможет разобраться в ряде пунктов задания10)

Продолжим рассмотрение примера про покупку трактора фермером.

Определим сумму выплат, дисконтированных по процентной ставке операции.

Представим, что фермер успешно ведет свою деятельность и имеет норму прибыли примерно 22% в год. Определим «экономически обоснован- ную» сумму общих выплат: сумму выплат, дисконтированных по процентной ставке, равной норме прибыли фермера. (Для простоты будем считать эту ставку номинальной для заданной схемы операции. Более правильным подхо- дом было бы рассмотрение этой ставки как эффективной и определение соот- ветствующей номинальной ставки операции).

Решение

Дисконтируем суммарные выплаты по кредиту по обеим схемам по двум

процентным ставкам: ставке кредитной операции

i₁  15%  0,15

в год и

ставке, соответствующей норме прибыли фермера

i₂  22%  0, 22

в год. При

этом будем учитывать, что проценты наращиваются раз в квартал.

То есть будем дисконтировать величины R_k

по формуле:

V_k

m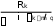
_1  _

 

^{где i– годовая ставка (} i₁ ^или i₂ ^{); m– число начислений процентов в год (в}

нашем примере начисления ежеквартальные,

m 4 ); q– число выплат в год

(в нашем примере выплаты раз в пол года,

^{q 2} ).

Дисконтирование будем проводить в MS Excel. Здесь приведем лишь не- сколько примеров аналитического вычисления:

1. 
   Дисконтированные по ставке
   

i₁  0,15

величины аннуитетного пла-

тежа в 7-м и 8-м полугодиях соответственно равны:

V₇ 



R<sub>7

0,15 </sub>74 2

_ 293245,55

_{ 0,15 }74 2

 175145,08

_1  _{4  }1  _{4 }

   

V₈ 



R<sub>8

0,15 </sub>84 2

_ 293245,55

_{ 0,15 }84 2

 162712,81

_1  _{4  }1  _{4 }

(берем
R₇  R₈  R

   

из первой части рассмотрения примера).

2. 
   ^{Дисконтированные по ставке} i₂  0, 22 ^{величины платежей в 5-м и 6-м}
   

полугодиях для дифференцированной схемы равны:

V₅ 



R<sub>5

0, 22 </sub>54 2

_ 291687,50

_{ 0, 22 }54 2

 170762,78

_1  _{4  }1  _{4 }

   

V₆ 



R<sub>6

0, 22 </sub>64 2

_ 276406, 25

_{ 0, 22 }64 2

 145384,58

_1  _{4  }1  _{4 }

(берем
R₅ ^и

   

R₆ ^{из второй части рассмотрения примера).}

Все остальные дисконтированные величины определяются аналогично или в MS Excel. Таблицы MS Excel с результатами расчетов и использованными формулами приведены ниже. В них же сразу сосчитаны суммы по датам всех величин. В целях идентификации данных для схемы аннуитета используется литера A, а для дифференцированной схемы литера D. Для первой ставки дис- контирования использована цифра 1, для второй – цифра 2. Таким образом, RA и RD – общие выплаты по схеме аннуитета и дифференцированной (они были определены ранее); VA1 и VD1 – те же выплаты, дисконтированные по ставке

i₁ ^{; VA2 и VD2 – те же выплаты, дисконтированные по ставке} i₂ ^.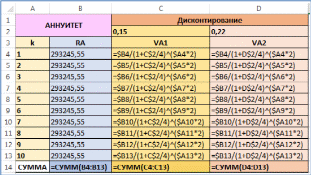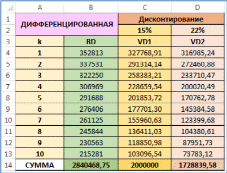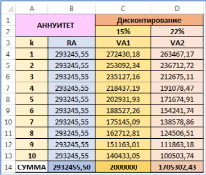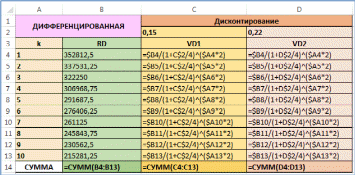

Сделаем несколько выводов:

1. 
   Сумма платежей, дисконтированных по исходной ставке операции для обеих схем равна величине займа. Это не совпадение, а строгая закономер- ность, определяемая условием кредита: вся кредитная операция равно- сильна занимаемой сумме с учетом дисконтирования по ставке и правилам кредита.
   
2. 
   Сумма дисконтированных выплат по ставке, более высокой, чем ставка кредита, приводит к большим значениям для дифференцированной схемы. Если бы мы проводили дисконтирование по меньшей ставке, то получили бы обратное соотношение (как пример можно рассматривать простую бух- галтерскую сумму эквивалентную дисконтированию по нулевой ставке). Данная закономерность обусловлена большими ранними выплатами при дифференцированной схеме и большими поздними выплатами при аннуи- тете. Таким образом, при большем временном падении ценности денег вы- годнее становится аннуитет и при меньшем падении – дифференцирован- ная схема.
   
3. 
   Обе суммы дисконтированных выплат при ставке 22% меньше исходной величины займа. Значит для фермера операция займа экономически вы- годна. Это обусловлено тем, что банковское наращение идет по меньшей ставке, чем нарастают прибыли фермера.