|
|
Шпора по физике [3 семестр]. Интерференция света световая волна
Электрон в атоме водорода находится в центральном
симметричном поле ядра. Поэтому его потенциальная
функция (см. рисунок). E0 при r∞, E - ∞ при r0.
U= - ze(c.2)/r, ▼ψ+ 2m(E+ ze(c.2)/r)ψ=0. Основные заключения, которые приводят к решению уравнения Шреддингера применительно к атому водорода: 1) электрон в атоме водорода обладает дискретным энергетическим спектром, при этом собственное значение энергии электрона En= - mz(c.2)e(c.4)/2n(c.2)π(c.2). Соотношения для энергии стационарного состояния электрона в атоме водорода совпадает с формулой теории Бора. Однако Бору для получения этого результата пришлось вводить априоли квантования. В квантовой механике этот результат получается логически при решении основного уравнения квантовой механики. 2) Собственные значения волновых функций, соответствующих этим энергиям, содержат 3 целочисленных параметра, которые носят название квантовых чисел, n – главное квантовое число, L – орбитальное (азимутальное) квантовое число, m – магнитное квантовое число.
n=1,2,3…, L0,…., (n-1), т.е. n значений, m= - L, …,0,…, + L т.е. (2L+1) значение. n=1,L=0,m=0; n=2,L=0,1,m= -1,0,1; n=3,L=0,1,2,m=-2,-1,0,1,2 …
Квантовые числа имеют определенный физический смысл, n определяет энергию стационарного состояния электрона в атоме или атома. L определяет величину орбитального механического момента на стационарной орбите, m определяет его проекцию на внешнее направление. В качестве внешнего направления z выбирается, как правило, направление внешнего электрического и магнитного полей. L(в) = h (в)√L(L+1)` - орбитальный момент импульса электрона в атоме, Lz=h(в)m – проекция L(в) на внешнее направление. Т.о. орбитальный момент импульса электрона в атоме, его проекция на внешнее направление, энергия состояния квантованы. 3) энергия состояния определяется только главным квантовым числом. Данному значению энергии En соответствуют волновые функции, определяющие состояние электрона, отличающиеся квантовыми числами L и m. Т.о. атом может обладать одинаковой энергией, находясь в различных состояниях. Число состояний с одинаковой энергией носит название кратности вырождения уровней или состояний, а сами уровни называются вырожденными. Кратность вырождения определяется Σ[L=0, n=1] (2L+1)=
=n(c.2); n=1 E1, n=2 E2 – 4 состояний, n=3 E3 – 9 состояний. Состояние электрона в атоме, определенное квантовым числом L=1, называется S-состоянием. L=1 S-состояние, L=2 P-состояние, L=3 d-состояние, L=4 f-состояние. Обычно перед символом состояния ставится значение главного квантового числа. Квадрат модуля волновой функции определяет плотность вероятности обнаружения электрона в различных элементах объема.
a0= r (индекс I)/2. Рассмотрим распределение
электрической плотности на различных расстояниях
от ядра для различных состояний. Пространственное
распределение электронной
плотности получим
вращая вокруг оси z.
Анализ этой зависимости позволяет провести некую аналогию между представлениями квантовой механики и боровской теории. Из 1-го графика следует, что чем больше n, тем на большем расстоянии от ядра плотность вероятности обнаружить электрон падает до нуля. Это совпадает с представлениями Бора о том, что с увеличением n увеличивается радиус электронной орбиты. Максимум плотности вероятности обнаружить электрон в различных оъемах пространства атома совпадает с точками, по которым проходят радиусы боровских орбит. В теории Бора вводится без доказательства главное квантовое число n, которое определяет энергию состояния и орбитальный момент импульса электрона. В квантовой механике квантовые числа n, L и m получаются логически, при решении основного уравнения в квантовой механике. Т.к. при движении электрона в атоме существенными становятся волновые свойства электрона, то квантовая механика абстрагируется в понятии орбитального движения электрона. Каждому энергетическому состоянию в квантовой механике соответствует волновая функция, квадрат модуля которой определяет плотность вероятности нахождения электрона в различных элементах объема. Эта плотность вероятности различна в различных элементах объема, т.е. электрон как бы размазан в пространстве, образуя электронное облако, размеры и форма которого определяется соответственно главным и орбитальным квантовыми числами, а магнитное квантовое число определяет ориентацию его в пространстве. В квантовой механики доказывается, что возможны лишь такие переходы между состояниями, при которых орбитальное квантовое число меняется на 1, ∆L=+ - 1 - правило отбора для орбитального квантового числа. Его существование вытекает из закона сохранения момента количества движения.
Т.к. фотон обладает импульсом, то при
испускании фотона атомом он как бы уносится
из атома. ∆L= -1, а при поглощении этот фотон
как бы приносится в атом ∆L=1. Тогда
энергетический спектр атома водорода:
(см. рисунок)
СПИН ЭЛЕКТРОНА. СПИНОВОЕ КВАНТОВОЕ ЧИСЛО. ОПЫТЫ ШТЕРНА, ГЕРЛАХА.
Из магнетизма известно, что с любым электрическим током связано магнитное поле, и следовательно, если атом или частица обладает отличным от нуля орбитальным механическим моментом, она должна обладать орбитальным магнитным моментом, ибо орбитальное движение электрона можно уподобить круговому току, сила которого определяется частотой вращения электрона. J=eν. Оба момента направлены в противоположную сторону и связаны геромагнитным соотношением.
М(в)= - (L/2mc)*L(в), L(в)=h(в)√L(L+1)`, Lz(в)=h(в)m,
M(в)= - Lh(в)√L(L+1)`/2mc, Mz(в)= - Lh(в)m/2mc, Lh(в)/2mc=Мб(в) – магнитон Бора – минимальный магнитный момент, которым может обладать атом. М(в)= - Мб(в) √L(L+1)`, Мz(в)= - Мб(в) m. Т.к. частица, обладающая не нулевым механическим орбитальным моментом, обладает и магнитным моментом, который квантован, то при помещении во внешнее магнитное поле она приобретает дополнительную энергию
∆U= - M(в)*H(в). Зависит от магнитного момента, направленности поля и угла между ними. В проекции на Н, ∆U= - Mz(в) * H(в) = Мб m H(в). Т.е. дополнительная энергия, которую приобретает частица во внешнем магнитном поле, квантована => под действием магнитного поля может происходить расщепление энергетических уровней или снятие вырождения уровня по магнитному квантовому числу.
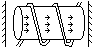
Т.е. вырожденные уровни расщепляются
на ряд подуровней. Впервые исследование
расщепления пучка нейтральных атомов и
молекул во внешнем магнитном поле было
проведено Штерном и Герлахом, которые в своих опытах пропускали пучки нейтральных атомов через неоднородное магнитное поле.
В неоднородном магнитном поле на электрон в атомах
действовала сила F=gradU= - gradM(в)H(в). Эта сила была в
состоянии расщепить пучки атомов в соответствии со значениями квантового числа m, определяющим число проекций на внешнее магнитное поле. Следовательно ожидать, что при прохождении через неоднородное магнитное поле пучка нейтральных атомов водорода, электроны, в которых состояние 1S с n=1 L=0, число возможных проекций магнитных моментов m=(2L+1)=1. Т.е. расщепление либо не должно было наблюдаться, либо, если предположить, что в пучке часть атомов водорода находится с электроном в p-состоянии (L=1), то число возможных пучков m=(2L+1)=3. Результаты опыта показали, что таких пучков всего лишь 2. Т.е. пучок атома водорода расщепляется на 2. => магнитный момент, обусловивший это расащепление, имеет 2 проекции на внешнее магнитное поле. Обозначим соответствующее квантовое число, описывающее эти процессы m (индекс S) = (2S+1)=2. S – спиновое квантовое число, соответствующее по аналогии с орбитальным квантовым числом L. S – квантовое число, определяющее величину собственного механического момента электрона в атоме. S=1/2, m (индекс S) = + - ½, т.е. собственный механический момент электрона в атоме водорода может быть ориентирован по полю и против него. По аналогии с орбитальным моментом: S=h(в)√S(S+1)`=h(в)√3/4`.
m (индекс z) = + - ½ h(в) – проекция собственного механического момента.
В квантовой механике спиновое квантовое число не учитывается. Первоначальная идея о существовании спина заключалась в том, что собственный механический момент электрона в атоме обусловлен вращением электрона вокруг собственной оси. Современные представления о спине следуют, что спин – необъемное свойство электрона или другой микрочастицы, такое же свойство, как заряд и масса.
ПРИНЦИП ПАУЛИ. ПЕРИОДИЧЕСКАЯ СИСТЕМА ЭЛЕМЕНТОВ МЕНДЕЛЕЕВА.
Состояние в квантовой механике описывается 4-мя квантовыми числами (см. предыдущий пункт). Если атомы находятся в невозбужденном состоянии, то казалось бы, что все они должны быть сосредоточены в состоянии 1S (n=1, L=0, m=0, S=1/2). Опыт показывает, что это не так. Согласно одному из основных законов квантовой механики – принципу Паули – в одном и том же атоме не может быть 2-х электронов, обладающих одинаковой совокупностью квантовых 4-х чисел или в одном и том же состоянии одновременно не могут находится 2 электрона. Число электронов с данным значением n определяется
2Σ[L=0, n-1](2L+1)=2n(c.2). Совокупность электронов в атоме с одинаковыми значениями n и L, образуют электронную оболочку. Совокупность электронных оболочек
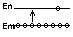
с одинаковым значением n,
образуют группу или слой.
Слоям дают следующие наименования: (см. рисунок). Как происходит заполнение электронами периодической таблицы Менделеева? Одной из своих задач физика видела объяснение закона периодической системы Менделеева. Рассмотрим заполнение электронами первых двух периодов таблицы Менделеева, начиная с простейшего атома водорода. Каждый последующий элемент будем получать из предыдущего, увеличивая заряд на 1 и добавляя 1 электрон, который будет в месте с минимальной энергией.
H (n=1, L=0, m=0, S=1/2) 1S, He (n=1, L=0, m=0, S=1/2, n=1, L=0, m=0, S=
= - ½) 1S(c.2). На атоме гелия заканчивается постройка k-слоя. У лития – 3-й электрон заполняет S-оболочку слоя лития. Третий электрон у лития слабее связан с ядром. Именно он отвечает за оптические, химические и электрические свойства и называется оптическим (валентным) электроном.
Ne – 1S(c.2) 2S(c.2) 2P(c.6). У неона, также как и у атома гелия, внешняя электронная оболочка полностью замкнута – заполнена электронами. Именно этим объясняются особые свойства инертных газов. Т.о. периодическая повторяемость свойств электронов таблицы Менделеева объясняется периодической повторяемостью электронных конфигураций внешних электронных оболочек. Периодическая таблица элементов строится 3-х основных положениях: 1) заряд ядра атома совпадает с порядковым номером элемента в таблице Менделеева. Каждый последующий элемент получается из предыдущего увеличением заряда ядра на 1 и добавлением одного элетрона. 2) С увеличением числа электронов в атоме каждый последующий электрон занимает доступное ему место с минимумом потенциальной энергии. 3) Распределение электронов по состояниям должно соответствовать принципу Пауля.
РЕНТГЕНОВСКОЕ ИЗЛУЧЕНИЕ (РИ)
РИ открыто В. Рентгеном в 1896 году. РИ обладает большой проникающей способностью, была обнаружена дифракция P лучей на пространственной дифракционной решетке и установлена λ=10(c.-10)м. Т.е. P кванты обладают очень высокой энергией => эти кванты могут испускаться вследствии перехода электронов в атоме между энергетическими состояниями, обладающими большими энергиями. Большими энергиями обладают состояния наиболее внутренних электронных слоев многоэлектронных атомов. P-трубка состоит из
3-х частей: вакумированного стеклянного сосуда с,
катода к, анода или антикатода А, выполенным из
металлов, атомы которых тжелые (обладают
большим количеством энергии электронов) – W,
Pt, Cu. Между К и А прикладывается U50кВ. Электроны, разогнанные силовым электрическим полем, бомбардируют А, который и испускает РИ.
|
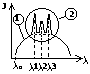   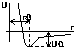 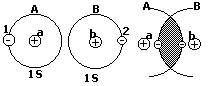 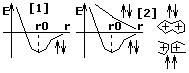  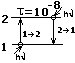  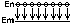 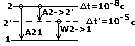     Исследования показали, что Р спектр состоит из Исследования показали, что Р спектр состоит из
сплошного спектра, характеризуемого в области коротких
длин волн, λ0 – коротковолновая граница сплошного
спектра, и монохроматический максимум интенсивности
cλ1, λ2, λ3 и т.д. Исследования показали, что
коротковолновая граница сплошного спектра не зависит от
природы вещества, материала А, но определяется
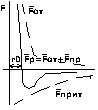
кинетической энергией электронов, бомбардирующих А, точнее U. При этом λ0=const/U (экспериментально). Объяснение существования λ0 сплошного спектра возможно на основе квантовых представлений. Если электроны, вылетающие из раскаленного К, преобретают в поле с разностью потенциалов U не очень высокую энергию, то при бомбардировании А, они могут оказаться пролетающими вблизи ядра атома. Электростатическое поле ядра тормозит эти электроны, в результате часть кинетической энергии электронов переходит в энергию излучения. mv(c.2)/2=eU. Какая часть энергиии электрона перейдет в энергию излучения зависит от того, как близок электрон пролетает вблизи ядра. В пределе вся энергия электрона переходит в энергию излучения.
eU=hν0, ν0=eU/h, λ0=hc/eU=const/U. По этой причине сплошной Р спектр называется тормозным Р спектром. Положением монохроматических максимумов в Р спектре не зависит от уинетической энергии электронов, но определяется природой атомов вещества А. Поэтому эта часть РИ – характеристическое РИ.
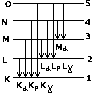
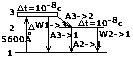
Атом А – многоэлектронный атом, у которого внутренние слои полностью заполнены электронами. Внешний электрон, обладающий большой энергией может выбить один из электронов с К или Л-слоя (нарисовать рисунок – атом +Ze, и вокруг него слои K, L, M, N). Выбитый электрон не может перейти на соседний слоя, т.к. у тяжелых атомов они полностью застроены электронами. Чаще всего выбитый электрон выходит за пределы, атома иногда – на внешний электронный слой, если там есть вакансии. Образовавшаяся вакансия в слое К является энергетически более выгодна для электрона из L-слоя. Происходит переход электрона с L-слоя в К-слой, сопровождающийся излучением Р-кванта. Харак-кие Р спектра содержат небольшое число спектральных линий, которые объединяются в группы, которые называются сериями (K-,L-,M-,N-серия и т.д.). К-серия возникает, если дырка-вакансия образуется в К-слое. У одних атомов эта вакансия заполняется электронами с L, M или N-слоя. Т.е.
К-серия возникает сразу вся. По мере увеличения
частоты Kα, Kp, Kγ. Если электрон перешол с
L-слоя, то в L-слое-дырка=>испускается L-серия.
Р спекрты отличаются простотой; практически сходны
для различных атомов, т.к. структура внешних
электронных слоев у различных атомов почти
одинакова. С увеличением заряда ядра z, Р спектр
смещается в торону кототких длин волн. Физик Мозли установил экспериментально в 1913 году закон √ν=c(z - δ) – закон Мозли. c,δ – некоторые констаты. В соответствии с этим законом частота Kα линии определяется, ν (индекс kα)=R’ (z – 1)(c.2) (1/(1(c.2)) – 1/(2 (c.2))), R’=R*c,
ν (индекс kβ)=R’ (z – 1)(c.2) (1/1(c.2) – 1/3(c.2)),
ν (индекс Lα)=R’ (z – 7,5)(c.2) (1/2(c.2) – 1/3(c.2)), ν =R’(z – δ)(c.2) (1/m(c.2) – 1/n(c.2)). Постоянная δ носит название констаты экранирования. Появление δ в этих соотношениях связано с тем, что переход электронов между внутренними электронными слоями в тяжелых атомах происходят в сильном электростатическом поле вещества, которое существенно ослабляется наличием всех других электронов т.е. экранируются другие электроны.
| |
|
|
 Скачать 1.6 Mb.
Скачать 1.6 Mb.