Дипломная работа по методике математика. Диплом_Просветов ДВ. Изучение производной в курсе математики средней школы
 Скачать 2.34 Mb. Скачать 2.34 Mb.
|
Глава 1. Теоретическое обоснование производной1.1. Понятие производной функцииПусть нам дана некая функция  , которая определена в обозначенной области значения аргумента. Выбирая некую точку , которая определена в обозначенной области значения аргумента. Выбирая некую точку 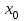 из заданной области, дадим из заданной области, дадим 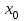 ей некое приращение ей некое приращение 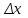 , которое будет отличным от нуля (причем таким образом, чтобы точка выбранная нами точка , которое будет отличным от нуля (причем таким образом, чтобы точка выбранная нами точка 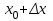 лежала именно в области определения данной функции). лежала именно в области определения данной функции). 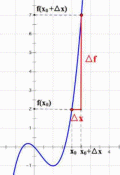 Рис. 1 Вычислив приращение данной функции 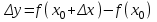 и составив отношение приращения функции к приращению аргумента, получим следующее равенство Данное отношение является некой функцией с аргументом 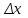 . . Может случиться то, что данная функция будет иметь предел при 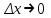 , то есть, что существует следующий предел функции: , то есть, что существует следующий предел функции:Именно этот предел мы и будем называть производной от данной функции в некой точке 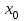 . .Замечание. Производная от некой функции  в заданной точке в заданной точке 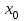 можно определять также следующим образом: можно определять также следующим образом:В действительности, производная некой функции  в заданной точке в заданной точке 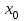 будет представлять собой следующее соотношение: будет представлять собой следующее соотношение:Обозначим 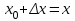 , тогда , тогда 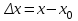 , причем при , причем при 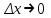 , , 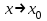 . Отсюда следует, что: . Отсюда следует, что:Данную форму записи производной функции в заданной точке 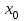 будем использовать и далее в данной работе. будем использовать и далее в данной работе.«Предполагаем, что заданная функция  в каждой точке некой области D будет иметь производную. Тогда каждому в каждой точке некой области D будет иметь производную. Тогда каждому  из области D будет соответствовать свое значение этой производной, и тем самым на области D построится некоторая функция из области D будет соответствовать свое значение этой производной, и тем самым на области D построится некоторая функция 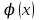 . Эта функция называется производной функцией от данной функции или просто производной от этой функции» [2]. . Эта функция называется производной функцией от данной функции или просто производной от этой функции» [2].Определение: Производной функцией от данной функции  называется (при переменном называется (при переменном  ) предел отношения приращения функции ) предел отношения приращения функции  к приращению ее аргумента, когда последнее стремиться к нулю1. к приращению ее аргумента, когда последнее стремиться к нулю1.Характеристику производной функции от функции  принято обозначать через принято обозначать через 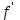 , так что , так чтоИначе производную от  обозначают через обозначают через 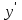 , а также ее можно обозначить следующим образом , а также ее можно обозначить следующим образом 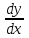 . .Таким образом, для того чтобы вычислить производную для заданной функции  , можно воспользоваться именно самим определение производной, для этого необходимо: , можно воспользоваться именно самим определение производной, для этого необходимо:1) Произвольному значению аргумента  в области определения заданной функции задать некоторое приращение в области определения заданной функции задать некоторое приращение 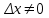 , а потом вычислить соответствующее приращение заданной функции: , а потом вычислить соответствующее приращение заданной функции:2) Далее необходимо составить отношение 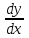 . .3) И переходят к решению предела данного отношения для 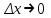 . .Те значения  , при которых данный предел будет существовать и составляют составят некую область D, в которой и существует производная , при которых данный предел будет существовать и составляют составят некую область D, в которой и существует производная 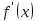 для задаваемой функции: для задаваемой функции:Операцию по отысканию производной для заданной функции называют дифференцированием2. Рассмотрим примеры нахождения производной по ее определению. Пример 1. Пускай некая функция будет задана на промежутке 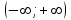 и соотношением и соотношением 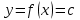 , для которой , для которой 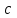 является некоторым постоянным числом. Необходимо найти производную для заданной функции. является некоторым постоянным числом. Необходимо найти производную для заданной функции.Решение: Возьмем некоторое число  с заданного промежутка число. Придадим ему некоторое приращение с заданного промежутка число. Придадим ему некоторое приращение 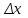 , и вычислим , и вычислим 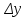 . . Поскольку 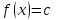 ( (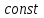 ), тогда и ), тогда и 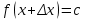 ; от сюда имеем, что ; от сюда имеем, что 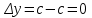 . . Теперь можем составить соотношение 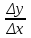 : : : :Далее переходим к пределу для 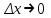 , можем найти для любого , можем найти для любого 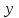 : :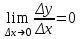 , т. е. , т. е. 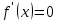 . .Таким образом, можем констатировать, что производная для функции, которая сохраняет постоянное значение, будет тождественно равна нулю. Данное определение записывают следующим образом и пишут: 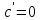 . Иными словами можем говорить о том, что производная от какого-либо постоянного числа равна нулю. . Иными словами можем говорить о том, что производная от какого-либо постоянного числа равна нулю.Пример 2. Пусть задана некая функция 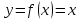 . Необходимо найти производную данной функции. . Необходимо найти производную данной функции.Решение: Выберем некоторое значение аргумента  , и дадим ему некого приращения , и дадим ему некого приращения 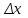 , далее проведем вычисление , далее проведем вычисление 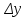 : : 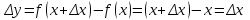 . .В результате имеем, что для каждого  : : 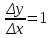 , именно поэтому и имеем равенство, что , именно поэтому и имеем равенство, что 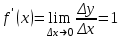 . .Таким образом нами было доказано, что производная для функции, которая является численно равной в каждой точке значениям своего аргумента, будет тождественно равной единице. Иными словами, можно сказать, что: производная аргумента (независимого переменного) будет равна единице. Данное утверждение можно записать следующим образом:  3. 3. |
