Дипломная работа по методике математика. Диплом_Просветов ДВ. Изучение производной в курсе математики средней школы
 Скачать 2.34 Mb. Скачать 2.34 Mb.
|
2.3. Геометрический подходВ первой главе нами была рассмотрена задача, условие которой заключается в нахождении касательной к кривой, которая является графиком функции  (на некотором интервале (на некотором интервале 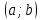 . Там мы дали определение касательной к указанной кривой в точке . Там мы дали определение касательной к указанной кривой в точке 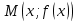 этой кривой. (Здесь этой кривой. (Здесь  - некоторое значение аргумента из интервала - некоторое значение аргумента из интервала 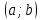 . см. рис. 20). Если произвольное приращение аргумента обозначить . см. рис. 20). Если произвольное приращение аргумента обозначить 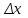 , а точку на кривой с координатами , а точку на кривой с координатами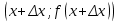 - символом - символом 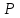 , то касательную, которая проходит через точку , то касательную, которая проходит через точку 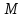 данной кривой, мы определили в качестве предельного положения секущей данной кривой, мы определили в качестве предельного положения секущей  при при 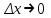 . .
сделали основанный на наглядных соображениях вывод: производная  равна угловому коэффициенту касательной в точке равна угловому коэффициенту касательной в точке 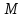 к графику функции к графику функции  .[24] .[24]Уточним указанные наглядные соображения. Предположим, что функция  имеет производную в данной точке имеет производную в данной точке  . Таким образом, мы докажем: 1) что график функции . Таким образом, мы докажем: 1) что график функции  имеет касательную в данной точке имеет касательную в данной точке 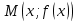 , 2) что угловой коэффициент указанной касательной равен , 2) что угловой коэффициент указанной касательной равен 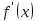 . .Утверждения 1) и 2) буде доказывать одновременно. Угол наклона секущей  к оси к оси 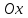 обозначим символом обозначим символом 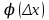 . Так как, угловой коэффициент секущей . Так как, угловой коэффициент секущей  (т. е. (т. е. 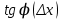 ) равен отношению ) равен отношению 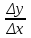 , то , то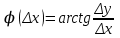 (1) (1)при любом достаточно малом 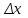 , который не равен нулю. Из того, что существует производная , который не равен нулю. Из того, что существует производная 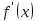 , то есть предельное значение , то есть предельное значение 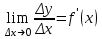 , из функция , из функция 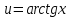 является непрерывной для всех значений аргумента, следует, что существует предельное значение функции (1) в точке является непрерывной для всех значений аргумента, следует, что существует предельное значение функции (1) в точке 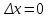 и равенство и равенство 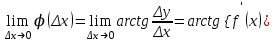 (2) (2)Равенство (2) доказывает, что существует предельное значение (при 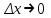 ) угла наклона секущей ) угла наклона секущей  , т. е. доказывает то, что существует касательная к точке , т. е. доказывает то, что существует касательная к точке 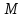 . Кроме того, из равенства (2) вытекает, что если обозначить угол наклона касательной через . Кроме того, из равенства (2) вытекает, что если обозначить угол наклона касательной через 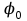 , то , то 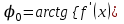 , т. е. , т. е. 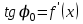 . . |

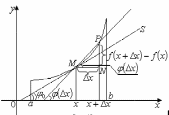
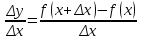 . Из этого факта и из того, что в пределе при
. Из этого факта и из того, что в пределе при