Дипломная работа по методике математика. Диплом_Просветов ДВ. Изучение производной в курсе математики средней школы
 Скачать 2.34 Mb. Скачать 2.34 Mb.
|
1.4. Монотонность функции«Изучая поведение функции в зависимости от того, как изменяется независимая переменная, предполагается, что во всей области определения функции независимая переменная монотонно возрастает, то есть, каждое ее следующее значение больше, чем предыдущее» [1]. Если при этом последовательные значения функции также возрастают, то функцию считают возрастающей, а если убывают - убывающей6. Есть определенные функции, которые во всей своей области определения меняются монотонно – только возрастают или только убывают. Например, 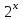 , ,  . .«Но многие функции изменяются не монотонно. В одних интервалах изменения независимой переменной они возрастают, а в других – убывают. Например, 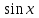 , , Возрастание и убывание функции 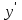 : если в некотором интервале : если в некотором интервале  , то функция возрастает, а если , то функция возрастает, а если 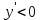 , то функция убывает в этом интервале.7 , то функция убывает в этом интервале.7Пример. На рисунке есть график функции у = f(х), которая определена на интервале (—4; 10). Необходимо найти число целых точек, в которых производная функции f(x) является отрицательной. 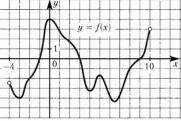 Рис. 8 Решение: Производная функции является отрицательной в том случае, когда функция убывает. На рисунке выделены цветом те области, где функция f(х) убывает: 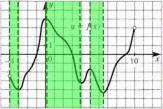 Рис.9 В этой области убывания функции f(x) находятся 4 целых значения х. 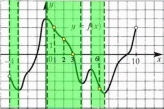 Рис.10 Ответ: 4. 1.5. Экстремум функций. Схема исследования дифференцируемой функции на максимум и минимум с помощью производной«Определение. Функция  в точке в точке 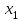 имеет максимум (maximum), если значение функции имеет максимум (maximum), если значение функции  в точке в точке 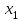 больше, чем ее значения во всех точках некоторого интервала, содержащего точку больше, чем ее значения во всех точках некоторого интервала, содержащего точку 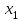 . Иначе говоря, функция . Иначе говоря, функция  имеет максимум при имеет максимум при 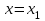 , если , если  при любых при любых 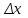 (положительных и отрицательных), достаточно малых по абсолютной величине» [1] . (положительных и отрицательных), достаточно малых по абсолютной величине» [1] .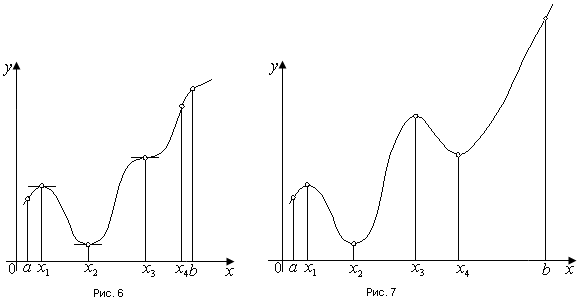 Рис. 11 Рис. 12 Так, например, функция  , график которой изображен на рис. 11, имеет максимум при , график которой изображен на рис. 11, имеет максимум при 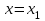 . . «Определение. Функция  имеет минимум (minimum) при имеет минимум (minimum) при  , если , если 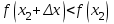 при любых при любых 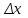 (положительных и отрицательных), достаточно малых по абсолютной величине (рис. 11)» [1]. (положительных и отрицательных), достаточно малых по абсолютной величине (рис. 11)» [1].В связи с определениями максимума и минимума следует обратить внимание на следующие обстоятельства. «1. Функция, определенная на отрезке, может достигать максимума и минимума только при значениях  , заключенных внутри рассматриваемого отрезка» [1]. , заключенных внутри рассматриваемого отрезка» [1].«2. Максимум и минимум функции не являются соответственно ее наибольшим и наименьшим значениями на рассматриваемом отрезке: в точке максимума функция имеет наибольшее значение лишь по сравнению с теми значениями, которые она имеет во всех точках, достаточно близких к точке максимума, а в точке минимума – наименьшее значение лишь по сравнению с теми значениями, которые она имеет во всех точках, достаточно близких к точке минимума» [1]. Так на рис. 12 изображена функция, определенная на отрезке 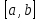 , которая при , которая при 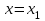 и и  имеет максимум, при имеет максимум, при  и и  имеет минимум, но минимум функции при имеет минимум, но минимум функции при  больше максимума функции при больше максимума функции при 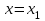 . При . При 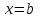 значение функции больше любого максимума функции на рассматриваемом отрезке. значение функции больше любого максимума функции на рассматриваемом отрезке.Максимумы и минимумы функции называют экстремумами или экстремальными значениями функции8. «Экстремальные значения функции и их расположение на отрезке 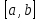 в известной степени характеризуют изменение функции в зависимости от изменения аргумента» [15]. в известной степени характеризуют изменение функции в зависимости от изменения аргумента» [15].Теорема (необходимое условие существования экстремума). Если дифференцируемая функция  имеет в точке имеет в точке 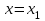 максимум или минимум, то ее производная обращается в нуль в этой точке, т. е. максимум или минимум, то ее производная обращается в нуль в этой точке, т. е.  . .Доказательство. «Предположим для определенности, что в точке 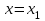 функция имеет максимум. Тогда при достаточно малых по абсолютному значению приращениях функция имеет максимум. Тогда при достаточно малых по абсолютному значению приращениях 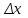 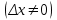 имеет место имеет место  , т. е. , т. е.  . Но тогда знак отношения . Но тогда знак отношения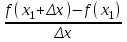 определяется знаком 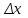 , а именно: , а именно: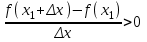 , при , при  , ,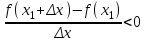 , при , при  » [1]. » [1].Согласно определению производной имеем Если  имеет производную при имеет производную при 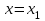 , то предел, стоящий справа, не зависит от того, как , то предел, стоящий справа, не зависит от того, как 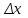 стремится к нулю (оставаясь положительным или отрицательным). стремится к нулю (оставаясь положительным или отрицательным).Но если 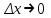 , оставаясь отрицательным, то , оставаясь отрицательным, то  . Если же . Если же 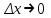 , оставаясь положительным, то , оставаясь положительным, то 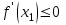 . .Так как 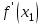 есть определенное число, не зависящее от способа стремления есть определенное число, не зависящее от способа стремления 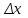 к нулю, то два последних неравенства совместимы только в том случае, если к нулю, то два последних неравенства совместимы только в том случае, если  . .Аналогичным образом теорема доказывается и для случая минимума функции. «Доказанной теореме соответствует следующий геометрический факт: если в точках максимума и минимума функция  имеет производную, то касательная к кривой имеет производную, то касательная к кривой  в этих точках параллельна оси в этих точках параллельна оси 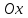 . Из того, . Из того,  , где - угол между касательной и осью , где - угол между касательной и осью 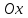 , следует, что , следует, что 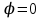 (рис. 8)» [4]. (рис. 8)» [4].«Следствие. Если при всех рассматриваемых значениях аргумента  функция функция  имеет производную, то она может иметь экстремум (максимум или минимум) только при тех значениях, при которых производная обращается в нуль» [5]. имеет производную, то она может иметь экстремум (максимум или минимум) только при тех значениях, при которых производная обращается в нуль» [5].«Обратное заключение неверно: не при всяком значении, при котором производная обращается в нуль, обязательно существует максимум или минимум. Так, на рис. 8 изображена функция, у которой при  производная обращается в нуль (касательная горизонтальна), но в этой точке функция не имеет ни максимума, ни минимума» [12]. производная обращается в нуль (касательная горизонтальна), но в этой точке функция не имеет ни максимума, ни минимума» [12].Функция может иметь экстремум лишь в двух случаях: либо в тех точках, где производная существует и равна нулю, либо в тех точках, где производная не существует9. «Если производная не существует в какой-либо точке (но существует в близлежащих точках), то в этой точке производная терпит разрыв» [21] . Значения аргумента, при которых производная обращается в нуль или терпит разрыв, называются критическими точками или критическими значениями. «Не при всяком критическом значении функция имеет максимум или минимум. Однако, если в какой-либо точке функция достигает максимума или минимума, то эта точка наверняка является критической. Поэтому для разыскания экстремума функции поступают следующим образом: находят все критические точки, а затем, исследуя отдельно каждую критическую точку, выясняют, будет ли в этой точке максимум или минимум функции, или же не будет ни максимума, ни минимума» [12] Исследование функции в критических точках опирается на следующие теоремы. Теорема (достаточные условия существования экстремума). «Пусть функция  непрерывна в некотором интервале, содержащем критическую точку непрерывна в некотором интервале, содержащем критическую точку 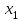 , и дифференцируема во всех точках этого интервала (кроме, быть может, самой точки , и дифференцируема во всех точках этого интервала (кроме, быть может, самой точки 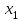 ). Если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то при ). Если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то при 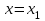 функция имеет максимум. Если же при переходе через точку функция имеет максимум. Если же при переходе через точку 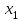 слева направо производная меняет знак с минуса на плюс, то функция имеет в этой точке минимум» [1]. слева направо производная меняет знак с минуса на плюс, то функция имеет в этой точке минимум» [1].Таким образом, если а)  при при 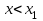 , ,  при при  , то в точке , то в точке 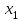 функция имеет максимум; функция имеет максимум;б)  при при 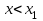 , ,  при при  , то в точке , то в точке 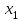 функция имеет минимум. При этом надо иметь в виду, что условия а) и б) должны выполняться для всех значений функция имеет минимум. При этом надо иметь в виду, что условия а) и б) должны выполняться для всех значений  , достаточно близких к , достаточно близких к 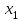 , т.е. во всех точках некоторой достаточно малой окрестности критической точки , т.е. во всех точках некоторой достаточно малой окрестности критической точки 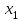 . .Доказательство. Предположим, что производная меняет знак с плюса на минус, т.е. что для всех  достаточно близких к точке достаточно близких к точке 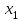 , имеем , имеем при при 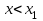 , f(x) < 0 при , f(x) < 0 при  . .Применяя теорему Лагранжа к разности 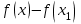 , получим , получим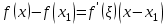 , ,где 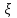 - точка, лежащая между - точка, лежащая между  и и 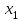 . .Пусть 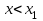 ; тогда ; тогда 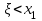 , ,  , ,  и, следовательно, и, следовательно, 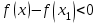 , или , или 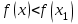 . .Пусть  ; тогда ; тогда 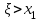 , ,  , ,  и, следовательно, и, следовательно,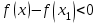 , или , или 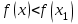 . .«Соотношения (1) и (2) показывают, что для всех значений  , достаточно близких к , достаточно близких к 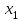 , значения функции меньше, чем значения функции в точке , значения функции меньше, чем значения функции в точке 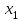 . Следовательно, в точке . Следовательно, в точке 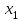 функция функция  имеет максимум» [2]. имеет максимум» [2].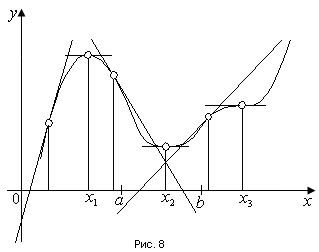 Рис.13 Аналогичным образом доказывается вторая часть теоремы о достаточном условии минимума. Рис. 13 наглядно иллюстрирует смысл теоремы. Пусть в точке 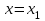 имеем имеем  и для всех и для всех  , достаточно близких к точке , достаточно близких к точке 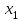 , выполняются неравенства , выполняются неравенства при при 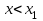 , ,  при при  . .Тогда при 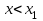 касательная к кривой образует с осью касательная к кривой образует с осью 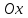 острый угол – функция возрастает, а при острый угол – функция возрастает, а при  касательная образует с осью касательная образует с осью 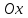 тупой угол – функция убывает; при тупой угол – функция убывает; при 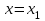 функция переходит от возрастания к убыванию, т.е. имеет максимум. функция переходит от возрастания к убыванию, т.е. имеет максимум.Если в точке  имеем имеем  и для всех значений и для всех значений  , достаточно близких к точке , достаточно близких к точке  , выполняются неравенства , выполняются неравенства при при  , ,  при при 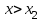 , ,то при  касательная к кривой образует с осью касательная к кривой образует с осью 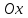 тупой угол – функция убывает, а при тупой угол – функция убывает, а при 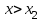 касательная образует с осью касательная образует с осью 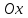 острый угол – функция возрастает. При острый угол – функция возрастает. При  функция переходит от убывания к возрастанию, т.е. имеет минимум. функция переходит от убывания к возрастанию, т.е. имеет минимум.Если при  имеем имеем 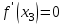 и для всех значений и для всех значений  , , достаточно близких к точке , , достаточно близких к точке 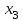 , выполняются неравенства , выполняются неравенства при при  , ,  при при  , ,то функция возрастает как при  , так и при , так и при  . Следовательно, при . Следовательно, при  функция не имеет ни максимума, ни минимума. функция не имеет ни максимума, ни минимума.Сформулируем правило для исследования дифференцируемой функции  на максимум и минимум10: на максимум и минимум10:Ищем первую производную функции, т.е. 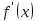 . .Находим критические значения аргумента x; для этого: а) приравниваем первую производную к нулю и находим действительные корни полученного уравнения 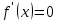 ; ;б) находим значения x, при которых производная 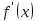 терпит разрыв. терпит разрыв.«1. Исследуем знак производной слева и справа от критической точки. Так как знак производной остается постоянным в интервале между двумя критическими точками, то для исследования знака производной слева и справа, например, от критической точки  (рис. 8) достаточно определить знак производной в точках и ( (рис. 8) достаточно определить знак производной в точках и (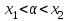 , , 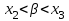 , где , где 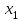 и и 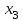 – ближайшие критические точки)» [19]. – ближайшие критические точки)» [19].2. Вычисляем значение функции  при каждом критическом значении аргумента. при каждом критическом значении аргумента.Таким образом, имеем следующее схематическое изображение возможных случаев:
Пример 1. На рисунке изображен график функции у = f'(х), которая является производной функции /(х) и определена на интервале (-10; 14). Необходимо найти точки максимума функции f(х), которые принадлежат отрезку [—8; 13]. 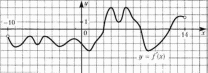 Рис. 14 Решение: поскольку на рисунке изображен график производной, то мы будем рассматривать только знаки и нули производной.  Рис.15 На рисунке на отрезке ([—8; 13]) существует 3 нуля у = f'(х). При этом производная меняет знак, переходя через них. Это и есть точки экстремума. Производная становится отрицательной, то есть, со знаком «-» в точке 8, которая помечена красным цветом, и меняет знак с «-» на знак «+» в двух точках: 3 и 12, которые помечены синим цветом. Следует объяснить это. Когда функция переходит через точку максимума, она меняет возрастание на убывание, а производная – знак «+» на знак «-».[20] Таким образом, точка максимума одна и помечена красным цветом. Ответ: 1. | |||||||||||||||||||||||
