Дипломная работа по методике математика. Диплом_Просветов ДВ. Изучение производной в курсе математики средней школы
 Скачать 2.34 Mb. Скачать 2.34 Mb.
|
1.2. Геометрический, механический смысл1.2.1. Геометрический смысл производной«Производная имеет определенный геометрический смысл. Геометрическое истолкование производной тесно связано с понятием касательной к кривой. Пусть дана непрерывная функция  , график которой изображен на рисунке 1» [13]. , график которой изображен на рисунке 1» [13].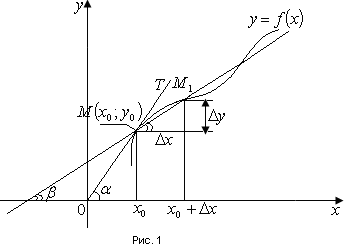 Рис. 2 «Дадим определение касательной к кривой в точке. Пусть 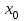 - абсцисса точки - абсцисса точки 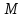 ; выберем на кривой точку ; выберем на кривой точку 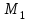 , абсцисса которой будет, очевидно, , абсцисса которой будет, очевидно, 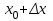 . Через точки . Через точки 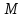 и и 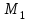 проведем прямую - она будет являться секущей к рассматриваемой кривой» [5]. проведем прямую - она будет являться секущей к рассматриваемой кривой» [5].Нетрудно видеть из чертежа, что угловой коэффициент секущей 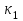 равен: равен: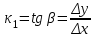 . .«Предположим теперь, что 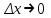 , т. е. что абсцисса точки , т. е. что абсцисса точки 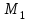 приближается к абсциссе точки приближается к абсциссе точки 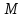 , а это в свою очередь означает, что точка , а это в свою очередь означает, что точка 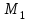 будет стремиться к точке будет стремиться к точке 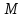 , оставаясь на кривой. Секущая будет вращаться около точки , оставаясь на кривой. Секущая будет вращаться около точки 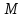 . Если при этом секущая стремится занять некоторое предельное положение . Если при этом секущая стремится занять некоторое предельное положение 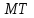 , для которого , для которого 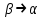 при при 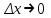 , то , то 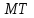 называют касательной к кривой в данной точке называют касательной к кривой в данной точке 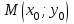 » [2]. » [2].Определение. «Касательной к кривой в точке 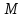 называют предельное положение секущей называют предельное положение секущей 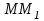 , когда точка , когда точка 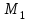 стремится к точке стремится к точке 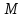 , оставаясь на кривой» [16]. , оставаясь на кривой» [16].Касательная представляет собой прямую, поэтому ее уравнение имеет вид: 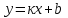 , ,где  - угловой коэффициент, который будем называть угловым коэффициентом касательной. Так как - угловой коэффициент, который будем называть угловым коэффициентом касательной. Так как 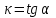 , то из определения касательной и непрерывности функции , то из определения касательной и непрерывности функции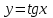 , ,  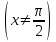 имеем: 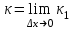 (1) (1)Пользуясь производной, можно найти значение  в заданной точке кривой. в заданной точке кривой.Теорема 1. Угловой коэффициент  касательной к кривой касательной к кривой  в точке в точке 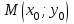 равен значению производной функции равен значению производной функции  при при  : :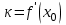 (2) (2)Доказательство. Согласно равенству (1) 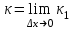 . .Из рисунка 1 видно, что  , ,следовательно, 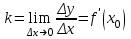 . .«Справедливо также утверждение: Если функция имеет производную в некоторой точке, то в соответствующей точке существует касательная к ее графику. Причем значение производной совпадает с угловым коэффициентом касательной» [1]. В этом заключается геометрический смысл производной. Зная угловой коэффициент касательной к кривой и точку касания, можно найти уравнение касательной. Теорема 2. Уравнение касательной к кривой  в точке в точке 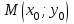 , где , где 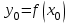 имеет вид: имеет вид: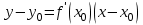 . (3) . (3)Доказательство. Чтобы найти уравнение касательной, нужно в уравнении прямой 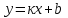 определить определить  и и 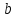 . Согласно выражению (2) . Согласно выражению (2) 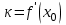 . .Чтобы найти 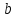 , воспользуемся тем, что касательная проходит через точку , воспользуемся тем, что касательная проходит через точку 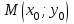 . Это означает, что координаты этой точки должны удовлетворять уравнению прямой, т. е. . Это означает, что координаты этой точки должны удовлетворять уравнению прямой, т. е.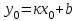 , ,откуда 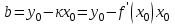 . .Подставив найденные значения  и и 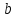 в уравнение прямой, получим уравнение касательной к кривой в ее точке в уравнение прямой, получим уравнение касательной к кривой в ее точке 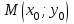 : :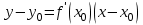 . .Пример 1. «Дан график функции у = f(х), которая определена на интервале (-5; 5). Он изображен на рисунке. Необходимо найти количество точек, в которых касательная к графику функции является параллельной прямой у = 6 или совпадает с ней» [1]. 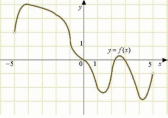 Рис. 3 Так, как касательная к графику функции f(x) является параллельной (или совпадает) прямой у = 6 (или у = kX + 6, k = 0), которая имеет угловой коэффициент k = 0, то касательная также имеет угловой коэффициент, который равняется 0. Поскольку угловой коэффициент k – это тангенс угла наклона касательной к оси (Ох), то касательная параллельна оси Ох. П 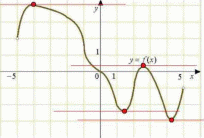 оэтому на графике следует найти точки максимума и минимума, то есть, точки экстремума, так как в данных точках касательные к графику функции f(х) являются параллельными оси (Ох). Рис. 4 Таких точек - 4. Ответ: 4. 1.2.2. Механический смысл производнойПусть уравнение 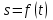 характеризует зависимость пути s от времени tв прямолинейном движении. По определению скорость движения в момент времени t задается равенством: характеризует зависимость пути s от времени tв прямолинейном движении. По определению скорость движения в момент времени t задается равенством: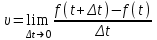 (в предположении, что последний предел существует). Но указанный предел есть как раз производная от функции 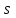 в точке в точке 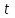 : :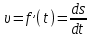 , ,или, как говорится обычно в физике: скорость прямолинейного движения есть производная от пути по времени4. Таково механическое истолкование понятия производной, чрезвычайно важное для физики, техники. «Задача об определении скорости движущейся точки в данный момент времени, как и задача о проведении касательной к данной кривой в данной точке, были теми задачами, которые привели в XVII в. к открытию дифференциального исчисления (Ньютон, Лейбниц)» [7]. |
