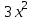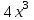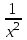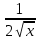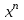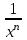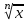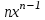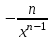Дипломная работа по методике математика. Диплом_Просветов ДВ. Изучение производной в курсе математики средней школы
 Скачать 2.34 Mb. Скачать 2.34 Mb.
|
2.2. Индуктивный способ введения понятия производнойТема «Производная и ее применение» изложена в современных школьных учебниках таким образом, что она дублирует дедуктивный подход вузов: сначала необходимо определить величины 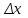 и и 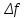 , а затем изучить отношение , а затем изучить отношение 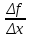 и рассмотреть его предел при и рассмотреть его предел при 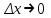 . После того, как формально определили . После того, как формально определили 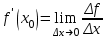 , как пример рассматриваются производные функций , как пример рассматриваются производные функций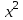 , ,  , , 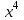 , , 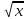 , , 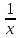 . . Дублирование вузовского подхода к изложению темы «Производная и ее применение» в современных школьных учебниках приводит к тому, что математику преподают формально. Академик В.И. Арнольд писал, что «выхолощенное и формализованное преподавание математики на всех уровнях стало системой. Самыми характерными предметами формализованного преподавания являются изобилие немотивированных определений и непонятных (хотя логически безупречных) доказательств, ... отсутствие в нематематических приложений и мотивировок понятий математики». Дедуктивный вузовский подход применяется к студентам 17-18 лет, которые уже определились с профессией. Выпускник средней школы имеет только 16 лет, и только начинает выбирать профессию. Она необязательно должна быть связана с математикой. Поэтому мы говорим не о математических классах, в которых можно предполагать знание теории вещественных чисел, предела и непрерывности, а о учащихся, которые с данными понятиями не знакомы. «Способ введения понятия производной, который предлагается, в отличие от вузовского дедуктивного называется индуктивным12. Его основная суть заключается в следующем. Основная задача о нахождении уравнения касательной к графику функции  в точке в точке 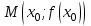 решается в начале для простейших известных школьникам функций решается в начале для простейших известных школьникам функций 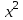 , ,  , , 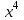 , , 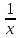 , , 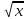 » [22]. » [22].Для того, чтобы найти уравнения касательной к графикам этих функций не требуется ни понятия приращения аргумента и функции, ни строгое определение предела, только для перехода к рассмотрению общего случая  необходимо вводить математический формализм, и к нему учащиеся будут готовы, поскольку они рассмотрят огромное количество примеров. Необходимо отметить, что вместе с уравнением касательных к графикам функций необходимо вводить математический формализм, и к нему учащиеся будут готовы, поскольку они рассмотрят огромное количество примеров. Необходимо отметить, что вместе с уравнением касательных к графикам функций 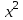 , ,  , , 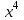 , , 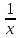 , , 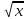 в точке в точке 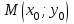 , указывается и способ их построения. , указывается и способ их построения.Когда ученики начнут изучать тему «Производная и ее применение», они будут знакомы с уравнением прямой в виде:  или или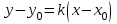 , (1) , (1)где 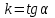 - угловой коэффициент, - угловой коэффициент, 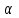 - угол между прямой и осью Оx, - угол между прямой и осью Оx, 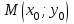 - точка, чрез которую проходит прямая. - точка, чрез которую проходит прямая.Учащиеся 10-го класса знают, что если прямая проходит через точки 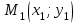 и и 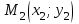 , то ее угловой коэффициент можно определить по формуле: , то ее угловой коэффициент можно определить по формуле: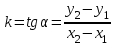 , (2) , (2)Из курса геометрии ученики знают об единственном примере касательной – касательной к окружности как прямая, которая имеет с окружностью общую точку, и только одну. Для того, чтобы построить касательную к окружности в точке М, необходимо провести прямую МТ перпендикулярно радиусу ОМ. Другие касательные ученикам неизвестны. Из всех элементарных функций учащимся известны функции 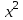 , ,  , , 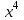 , , 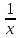 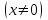 , , 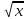  , а также основные тригонометрические функции: , а также основные тригонометрические функции: 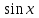 , , 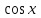 , , 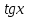 . . Определение производной. Угловой коэффициент касательной – это важная характеристика функции (достаточно вспомнить связь между касательной и скоростью). Учитывая данное обстоятельство, в математике вводится понятие производной. Рассмотрим функцию  и точку и точку 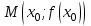 на ее графике. на ее графике.Определение: Угловой коэффициент касательной, которую провели к графику функции  в точке в точке 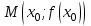 , называется производной функции , называется производной функции  при при  и обозначается символом и обозначается символом 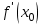 . Например, на рис. 37 . Например, на рис. 37 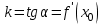 . . Рис. 15 Если точка 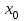 изменится, то изменит свое значение и производная изменится, то изменит свое значение и производная 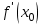 . Так, на рис. 15 . Так, на рис. 15 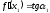 , а , а 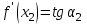 . .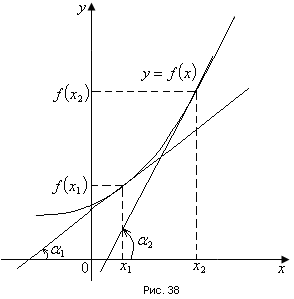 Рис. 16 Видно, что с изменением  изменится и производная. изменится и производная.Итак, производная функции  при при  - определенное число. Если меняется точка - определенное число. Если меняется точка , то меняется и производная данной функции , то меняется и производная данной функции  . .В соответствие каждой точке  ставим число ставим число 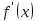 и получаем новую функцию, которая называется производной функции и получаем новую функцию, которая называется производной функции  . Штрих в обозначении новой функции говорит о том, что функция . Штрих в обозначении новой функции говорит о том, что функция 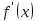 “произведена” из функции “произведена” из функции  . .Теперь собираем все угловые коэффициенты касательных, которые были получены выше. Сравнивая первый и третий столбцы таблице 1, получаем таблицу 2 производных. Таблица 2.
Используя понятие производной, уравнение касательной к графику функции  в точке в точке 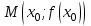 запишем в виде: запишем в виде: (19) (19)Все уравнения касательных, которые были получены выше, являются частными случаями формулы (19). В заключении следует сказать, что если ученики знают бином Ньютона и формулу 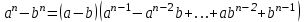 то с помощью способа, который был указан выше, они могут вычислить производные функций 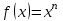 ; ; 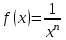 , , 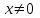 ; ; 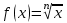 , ,  . Эти производные приведены в таблице 3. . Эти производные приведены в таблице 3.Таблица 3.
Для каждой функции, которую мы расмотрели, запишем уравнение касательной к графику в точке 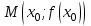 : :если 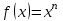 , то , то 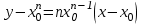 ; ;если 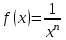 , то , то 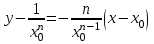 ; ;если 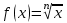 , то , то 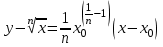  Рис 17 Рис. 18 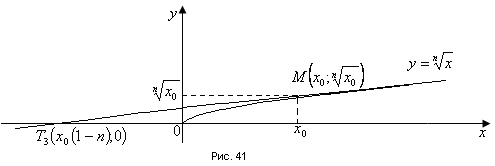 Рис. 19 Для того, чтобы построить касательные, сначала нужно найти точки 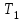 , , 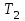 и и 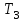 , их пересечения с осью , их пересечения с осью 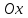 . Имеем: . Имеем: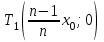 , , 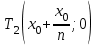 , , 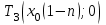 . .Каждую из найденных точек можно построить, используя теорему Фалеса, а также сдвиги по оси и отражение. Соединив точку касания 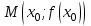 соответственно с точкой соответственно с точкой 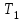 (рис.17), с точкой (рис.17), с точкой 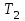 (рис. 18), с точкой (рис. 18), с точкой 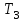 (рис. 19), получили искомые касательные. (рис. 19), получили искомые касательные. |